数据库一二三范式简单解释

第一范式

一个关系模式应当是一个五元组。
$R(U,D,DOM,F)$
这里：

• 关系名$R$是符号化的元组语义
• $U$为一组属性
• $D$为属性组$U$中的属性所来自的域
• $DOM$为属性到域的映射
• $F$为属性组$U$上的一组数据依赖

由于$D,DOM$与模式设计关系不大，因此在此把关系模式看作一个三元组：$<U,F>$
当且仅当$U$上的一个关系$r$满足$F$时，$r$成为关系模式$R<U,F>$的一个关系。

作为一个二维表，关系要符合一个最基本的条件：每一个分量必须是不可分的数据项
满足了这个条件的关系模式就属于第一范式（1NF）

数据依赖：
数据依赖是一个关系内部属性与属性之间的一种约束关系。
这种约束关系是通过属性间值的相等与否体现出来的数据间相关联系。

人们已经提出了许多种类型的数据依赖，其中最重要的是函数依赖和多值依赖

但是，这个关系模式存在以下问题：

数据冗余
每一个系的系主任姓名重复出现，重复次数与该系所有学生的课程成绩出现的次数相同。
这将浪费大量的存储空间。
更新异常
某系更换系主任后，必须修改与该系学生有关的每一个元组。

插入异常
如果一个系刚成立，尚无学生，则无法将这个系及其系主任的信息存入数据库。

删除异常
如果某个系的学生全部毕业了，则在删除该系学生信息的同时，这个系及其系主任的信息也丢掉了。

一个好的模式应当不会发生插入异常、删除异常和更新异常，数据冗余应尽可能少。

规范化

函数依赖

设$R(U)$是属性集$U$上的关系模式，$X,Y$是$U$的子集。若对于$R(U)$的任意一个可能的关系$r$，$r$中不可能存在两个元组在$X$上的属性值相等，而在$Y$上的属性值不等，则称$X$函数确定$Y$或$Y$函数依赖于$X$。
记作$X\to Y$。
函数依赖和别的数据依赖一样是语义范畴的概念，只能根据语义来确定一个函数依赖。

下面介绍一些术语和记号

• $X\to Y$，但$Y⊊X$,则称$X\to Y$是非平凡的函数依赖。

• $X\to Y$，但$Y\subseteq X$,则称$X\to Y$是平凡的函数依赖。
  对于任一关系模式，平凡函数依赖都是必然成立的，它不反映新的语义。若不特别声明，总是讨论平凡的函数依赖。

• 若$X\to Y$，则$X$称为这个函数依赖的决定属性组，也称为决定因素。

• 若$X\to Y$，$Y\to X$，则记作$X\leftarrow \to Y$

• 若$Y$函数不依赖于$X$，则记作$X\nrightarrow Y$

在$R(U)$中，如果$X\to Y$，并且对于$X$的任何一个真子集$X^{{}^{\prime }}$,都有$X^{{}^{\prime }}\nrightarrow Y$,则称$Y$对$X$完全函数依赖，记作$X{\to }^{F}Y$
如果$X\to Y$，但$Y$不完全函数依赖于$X$，则称$Y$对$X$部分函数依赖，记作$X{\to }^{P}Y$

码

码是关系模式中的一个重要概念。
设$K$为$R<U,F>$中的属性或属性组合，若$R{\to }^{F}U$，则$K$为$R$的候选码。
注意$U$是完全函数依赖于$K$，而不是部分函数依赖于$K$。一般地，如果$U$函数依赖于$K$，即$K\to U$，则$K$称为超码。

候选码是一类特殊的超码，即候选码的超集（如果存在）一定是超码，候选码的任何真子集一定不是超码。

若候选码多于一个，则选定其中的一个为主码。
包含在任何一个候选码中的属性称为主属性；不包含在任何候选码中的属性称为非主属性或非码属性。
最简单的情况，单个属性是码；
最极端的情况，整个属性组是码，称为全码。

范式

关系数据库中的关系是要满足一定要求的，满足不同程度要求的为不同范式。

一个低一级的范式的关系模式通过模式分解可以转换为若干高一级范式的关系模式的集合，这种过程就叫规范化。

第二范式

若$R\in 1NF$，且每一个非主属性完全函数依赖于任何一个候选码，则$R\in 2NF$。

第三范式

设关系模式$R<U,F>\in 1NF$,若$R$中不存在这样的码$X$，属性组$Y$及非主属性$Z(Z⊊Y)$使得$X\to Y$,$Y\to Z$,$Y\nrightarrow X$,则称$R<U,F>\in 3NF$。

扩充的第三范式

BCNF是修正的第三范式，有时也称为扩充的第三范式。
关系模式$R<U,F>\in 1NF$,若$X\to Y$且$Y⊊X$时$X$必含有码，则$R<U,F>\in BCNF$

由$NCNF$的定义可以得到结论，一个满足$BCNF$的关系模式有：

• 所有非主属性对每一个码都是完全函数依赖。
• 所有主属性对每一个不包含它的码也是完全函数依赖。
• 没有任何属性完全函数依赖于非码的任何一组属性。

多值依赖

设$R(U)$是属性集$U$上的一个关系模式。$X,Y,Z$是$U$的子集，并且$Z=U-X-Y$。关系模式$R(U)$中多值依赖$X\to \to Y$成立，当且仅当对$R(U)$的任一关系$r$，给定的一对$(x,z)$值，有一组$Y$的值，这组值仅仅决定于$x$值而与$z$值无关。

多值依赖具有以下性质：

1. 对称性
2. 传递性
3. 函数依赖可以看作是多值依赖的特殊情况

与函数依赖相比，多值依赖有下面两个基本的区别：

1. 多值依赖的有效性与属性集的范围有关
2. 见P188

4NF

$4NF$就是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖。

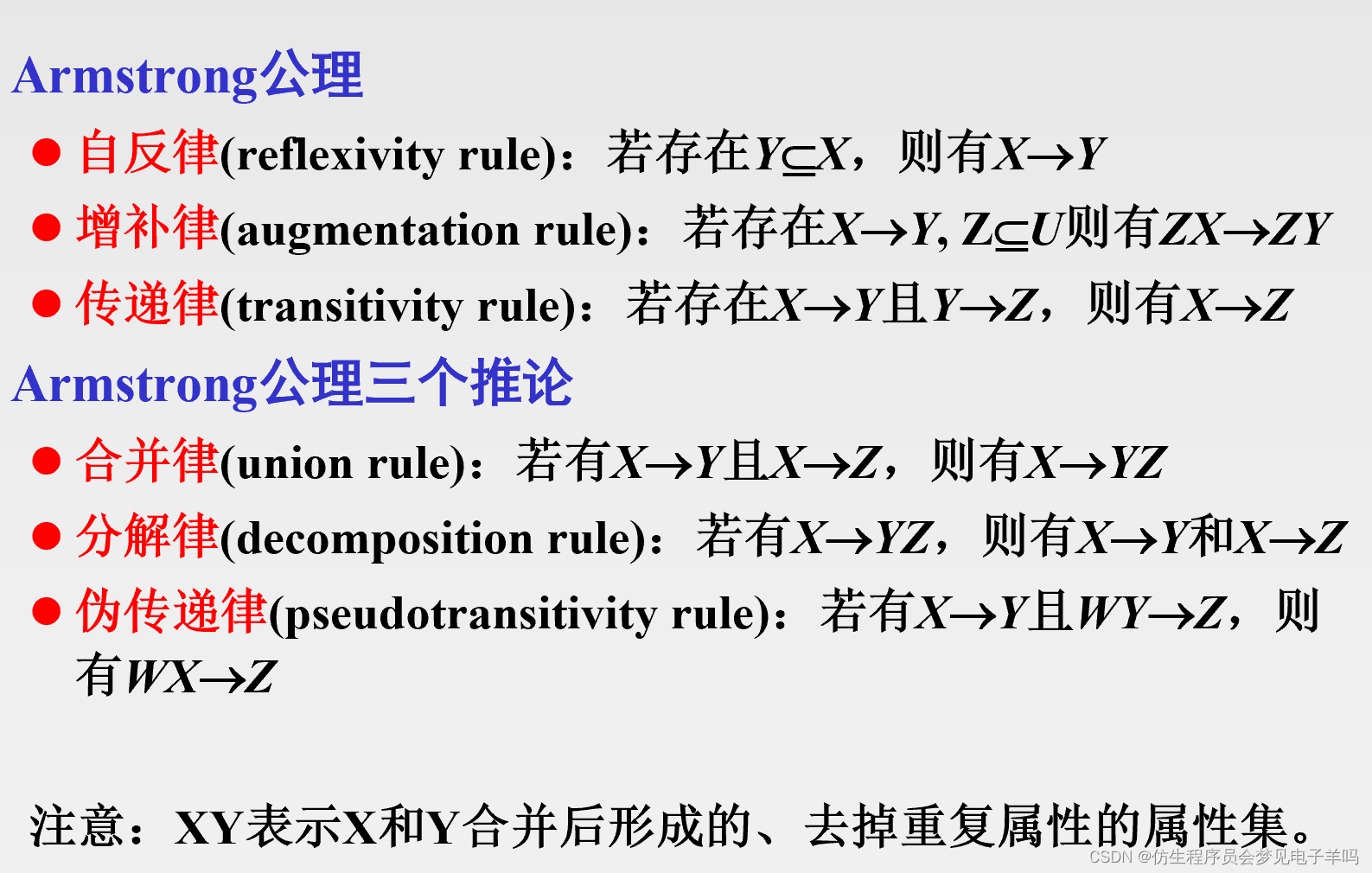
数据依赖的公理系统

$Armstrong$公理系统:设$U$为属性集总体，$F$是$U$上的一组函数依赖，于是有关系模式$R<U,F>$，对其来说有以下的推理法则：

• A1 自反律
• A2 增广律
• A3 传递律

根据$A1,A2,A3$这三条推理规则可以得到下面三条有用的推理规则：

• 合并规则
• 伪传递规则
• 分解规则