【基础算法系列】离散化与前缀和算法的运用

⭐️前面的话⭐️

本篇文章将主要介绍离散化算法，所谓离散化算法，就是将一个无限区间上散点的数，在不改变相对大小的情况下，映射到一个较小的区间当中，然后对这个较小的区间进行操作的过程就是离散化的过程，我将会以一道经典的离散化问题为栗子，介绍离散化（顺便介绍前缀和）算法，展示代码：Java/C++。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2022年11月20日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：无
💬参考在线编程网站：🌐牛客网🌐力扣🌐acwing
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

📌导航小助手📌

- 🍒1.算法简介
- 🍒2.离散化实战：区间和
- - 🍓题目详情
  - 🍓解题思路
  - 🍓代码实现

封面区

🍒1.算法简介

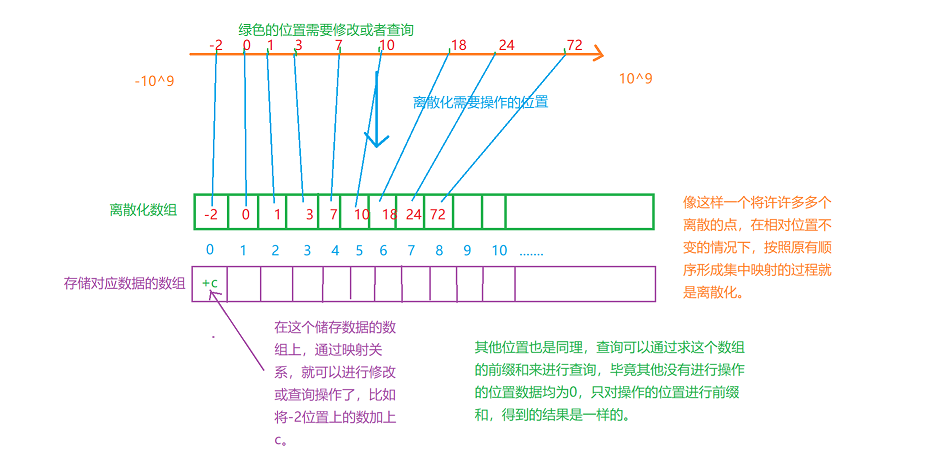
离散化算法，所谓离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。

就比如在一个很大的区间里面，有有限个数，比如[2333， 4888， 9888， 1212342313， 139， 10390， 8999932]这几个数，离散化就是将这些映射到另外一个区间中，在不改变相对大小的情况下，从小到大依次去重排序，得到序列[139, 2333, 4888, 9888, 10390, 8999932, 1212342313]，将这些数按照从小到大的顺序存入到数组当中，相对顺序不发生改变，但形成了与数组下标的映射，即139->0, 2333->1, 4888->2, 9888->3…这些数都按照大小顺序形成了映射，通过映射的下标，我们可以找到原来的那个数，如0就对应着139，也可以通过原数据通过二分的方法找到下标。

除了手动使用数组使元素与下标形式映射，还可以使用哈希表来进行建立映射关系。

离散化算法，常常会与其他算法结合起来使用，比如前缀和算法，差分等算法结合使用，一般使用在一个很大甚至无限大的区间中，但是需要查询或操作的数是有限的情形当中，遇到这种情况我们一般会使用离散化进行处理。

下面我们来看一道题目，来加深对离散化的理解。

🍒2.离散化实战：区间和

🍓题目详情

题目链接：802. 区间和

假定有一个无限长的数轴，数轴上每个坐标上的数都是 $0$ 。
现在，我们首先进行 $n$ 次操作，每次操作将某一位置 $x$ 上的数加 $c$ 。
接下来，进行 $m$ 次询问，每个询问包含两个整数 $l$ 和 $r$ ，你需要求出在区间 $[l, r]$ 之间的所有数的和。

输入格式：
第一行包含两个整数 $n$ 和 $m$ 。
接下来 $n$ 行，每行包含两个整数 $x$ 和 $c$ 。
再接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$ 。

输出格式：
共 $m$ 行，每行输出一个询问中所求的区间内数字和。

数据范围
$10^9≤x≤10^9$ ,
$1≤n,m≤10^5$ ,
$10^9≤l≤r≤10^9$ ,
$- 10000 \leq c \leq 10000$
输入样例：

输出样例：

8
0
5

🍓解题思路

题目的意思非常简单，就是先对一个很大的区间（初始值均为0）进行n次的修改操作（就是随机对区间内的某一个坐标进行加上一个数c的操作），修改操作结束后再进行m次的查询操作，每次需要返回区间 $[l, r]$ 上所有值的和。

根据题目所给的限制条件 $1<=n,m<10^5$ ，不难计算出总操作次数不会超过 $\times 10^5$ 次，也就是说，最多只会有 $N$ 坐标位置的数被修改或者查询，所以我们可以考虑使用离散化进行处理，我们可以申请一个大小为 $N$ 的数组，按照大小顺序存储所有进行过操作（包括修改和查询）的位置，这样就将原来大小很大的区间压缩到了一个比较小的区间，再建一个大小为 $N$ 的数组用来储存这些位置上的值，在这个数组上进行修改和查询操作。

由于我们还需要进行区间和的查询，因此还需要一个 $N + 1$ 大小的前缀和数组。

所以我们可以预先定义一下：

    public static final int N = (int) 3e5 + 233;
    //储存离散化后的数据
    public static int[] a = new int[N];
    //储存前缀和
    public static int[] s = new int[N];
    //储存原来排序去重可能访问的位置
    public static TreeSet<Integer> ts = new TreeSet<>();
    public static List<Integer> list;
    //储存修改的操作
    public static List<int[]> add = new ArrayList<>();
    public static List<int[]> query = new ArrayList<>();

c++也有哦：

const int N = (int) 3e5 + 233;
//离散化数组与前缀和数组
int a[N], s[N];
//使用pair进行储存
typedef pair<int, int> PAI;
//储存所有修改，查询的位置
vector<int> alls;
//分别储存修改和查询信息
vector<PAI> add, query;

那如何如果原位置找到离散化数组中的下标呢？很简单，因为数组是有序的，所以我们可以通过二分的方式找到对应的下标。

二分代码如下：
Java版本：

    //二分法找x位置在离散化数组中的下标
    private static int find(int x) {
        int l = 0;
        int r =ts.size() - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (list.get(mid) >= x) r = mid;
            else l = mid + 1;
        }
        //返回下标，为了前缀和查询方便，我们返回下标+1
        return l + 1;
    }

c++版本：

//使用二分实现查找离散化数组的下标
int find(int x) 
{
    int l = 0;
    int r = alls.size() - 1;
    while (l < r)
    {
        int mid = (l + r) >> 1;
        //寻找第一个大于或等于x在alls中的下标
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    //返回下标，为了前缀和查询方便，我们返回下标+1
    return l + 1;
}

对于区间查询，我们可以结合前缀和来进行实现，我们可以直接对离散化所映射储存数据的那个数组直接求 $n$ 次修改操作后的前缀和，因为原来区间内所有的初始值均为 $0$ ，所有经过 $n$ 次的单点修改后，对离散化所储存的数据求前缀和和对原来区间求前缀和得到的结果是一样的。

顺便在这里讲一下前缀和吧，所谓前缀和，就是将区间内的前 $i$ 个数加起来的数就是前缀和，对数组所有位置求的前缀和组成的数组叫做前缀和数组。

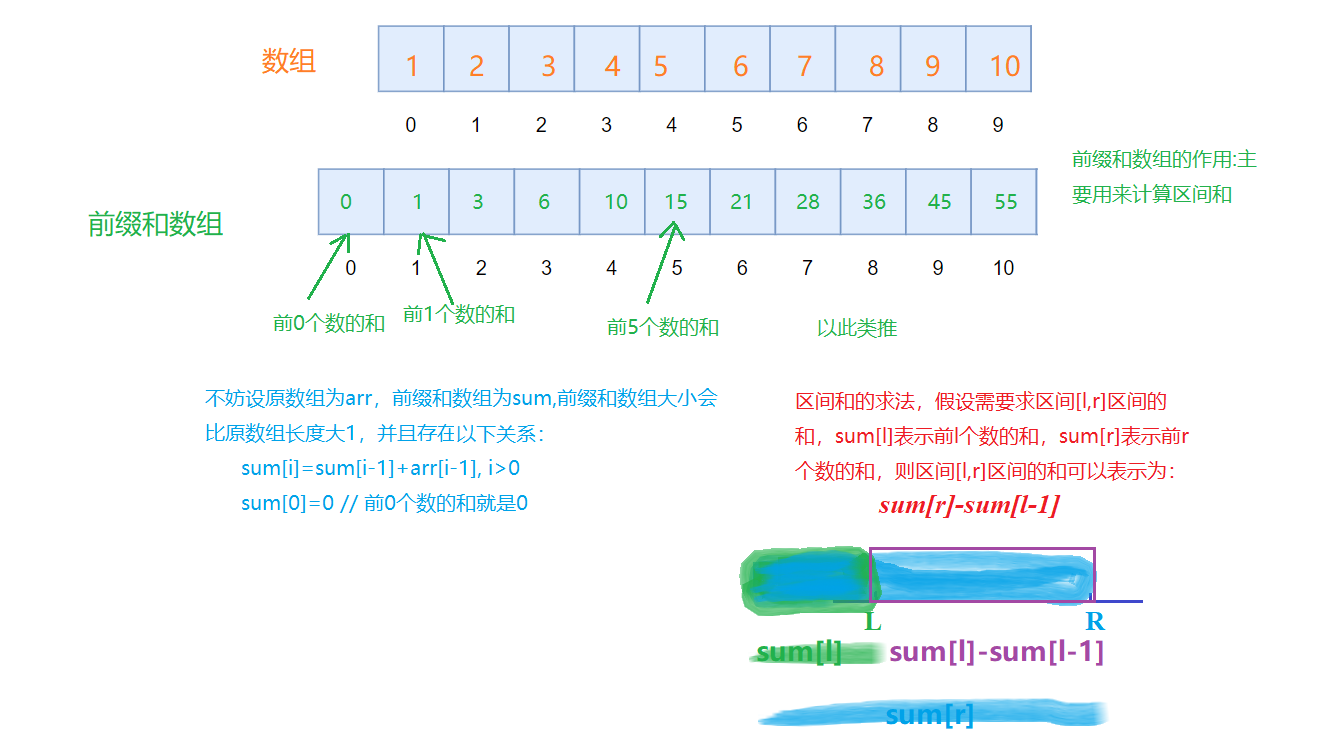
不妨设原数组为 $a r r$ ，前缀和数组为 $s u m$ ，则根据前缀和 $i$ 下标储存的是原数组 $a r r$ 前 $i$ 个元素的和可以知道：
$s u m [i] = s u m [i - 1] + a r r [i - 1] ，其中 i > 0$

前缀和最大的优势就是可以直接得到某一个区间的和。

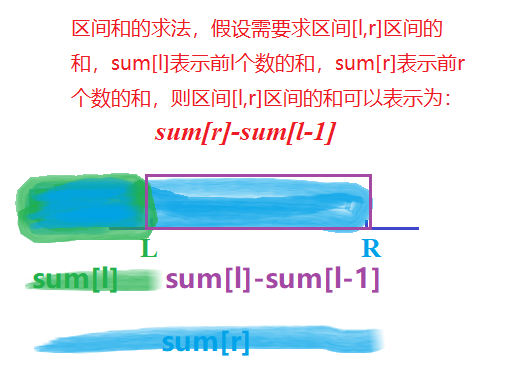
下面我们来写代码，通过代码来实现我们的逻辑。

🍓代码实现

java版本：

import java.util.*;

class Main {
    public static final int N = (int) 3e5 + 233;
    //储存离散化后的数据
    public static int[] a = new int[N];
    //储存前缀和
    public static int[] s = new int[N];
    //储存原来排序去重可能访问的位置
    public static TreeSet<Integer> ts = new TreeSet<>();
    public static List<Integer> list;
    //储存修改的操作
    public static List<int[]> add = new ArrayList<>();
    public static List<int[]> query = new ArrayList<>();
    
    //二分法找x位置在离散化数组中的下标
    private static int find(int x) {
        int l = 0;
        int r =ts.size() - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (list.get(mid) >= x) r = mid;
            else l = mid + 1;
        }
        return l + 1;
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt();
        int m = sc.nextInt();
        
    //输入修改数据
    for (int i = 0; i < n; ++i) {
        int x = sc.nextInt();
        int c = sc.nextInt();
        ts.add(x);
        
        add.add(new int[]{x, c});
    }
    //输入查询数据
    for (int i = 0; i < m; ++i) {
        int l = sc.nextInt();
        int r = sc.nextInt();
        
        ts.add(l);
        ts.add(r);
        
        query.add(new int[]{l, r});
    }
    
    //修改离散化的下标的数据
    //因为set不支持随机访问，我们使用它来构造一个list
    list = new ArrayList<>(ts);
    //遍历修改操作，进行单点修改
    for (int[] item : add) {
        int x = find(item[0]);
        int c = item[1];
        
        a[x] += c;
    }
    
    //求前缀和
    for (int i = 1; i <= ts.size(); ++i) {
        s[i] = s[i - 1] + a[i];
    }
    
    //输出离散化后区间的和
    for (int[] item : query) {
        int l = find(item[0]);
        int r = find(item[1]);
        
        int ans = s[r] - s[l - 1]; 
        System.out.println(ans);
    }
    
    }
}

C++代码实现：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int N = (int) 3e5 + 233;
//离散化数组与前缀和数组
int a[N], s[N];
//使用pair进行储存
typedef pair<int, int> PAI;
//储存所有修改，查询的位置
vector<int> alls;
//分别储存修改和查询信息
vector<PAI> add, query;

//使用二分实现查找离散化数组的下标
int find(int x) 
{
    int l = 0;
    int r = alls.size() - 1;
    while (l < r)
    {
        int mid = (l + r) >> 1;
        //寻找第一个大于或等于x在alls中的下标
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    //返回下标，为了前缀和查询方便，我们返回下标+1
    return l + 1;
}

int n, m;
int main()
{
    //读入数据
    cin >> n >> m;
    for (int i = 0; i < n; ++i)
    {
        int x, c;
        cin >> x >> c;
        alls.push_back(x);
        add.push_back({x, c});
    }
    //读入查询数据
    for (int i = 0; i < m; ++i)
    {
        int l, r;
        cin >> l >> r;
        alls.push_back(l);
        alls.push_back(r);
        
        query.push_back({l, r});
    }
    //离散化，1.排序 2.去重 Java中就是treeset
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    
    //映射+二分查找+修改
    for (PAI item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
        //cout << a[x] << endl;
    }
    //求前缀和
    for (int i = 1; i <= alls.size(); ++i)
    {
        //注意在这里 离散化数据数组从1位置开始存数据 所以s[i]=s[i-1]+a[i]
        s[i] = s[i - 1] + a[i];
        //cout << s[i] << endl;
    }
    
    //输出区间和
    for (PAI item : query)
    {
        int l = find(item.first);
        int r = find(item.second);
        
        cout << s[r] - s[l - 1] << endl;
    }
    
    return 0;
}