数据结构：栈和队列

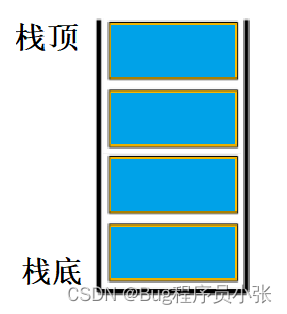
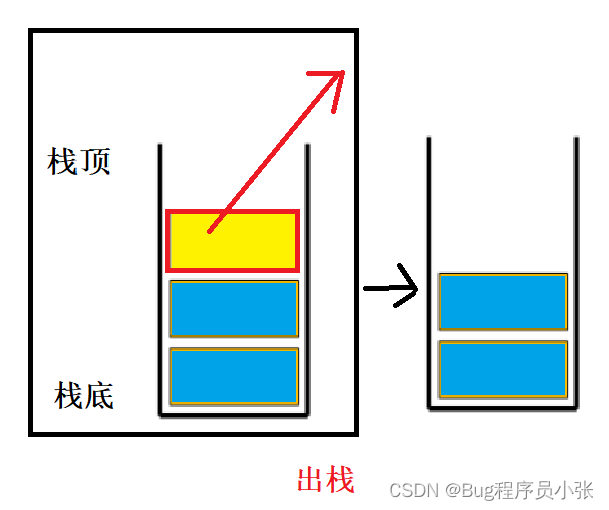
栈是一种特殊的线性结构，只允许在栈顶进行进行插入和删除操作。

进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。 栈中的数据元素遵守后进先出（先进后出） LIFO （ Last In First Out ）的原则。

类比成将子弹压入弹夹和子弹激发的过程，后压入弹夹的子弹要先被激发。而先压入的子弹更接近弹夹的底部，相对来说激发的顺序就要靠后。

栈的实现可以使用数组或者链表，下面的代码实现采用的是数组。

功能预览：

// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空
bool StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);

栈的实现：物理结构

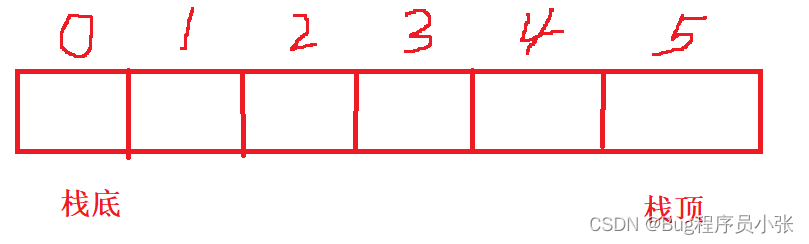
栈的实现类似于顺序表。成员方面，处了数组以外，还需要capacity记录栈的容量。top表示栈顶或者栈顶的下一个位置（取决与top的初始值）。如果top的初始值为0的话，好像top的值和顺序表中的size值相同。但还是要注意一下，top所表示的意义和顺序表完全不同。
typedef int STDataType;
typedef struct Stack
{
	STDataType* arr;
	int top; // 栈顶
	int capacity; // 容量
}Stack;

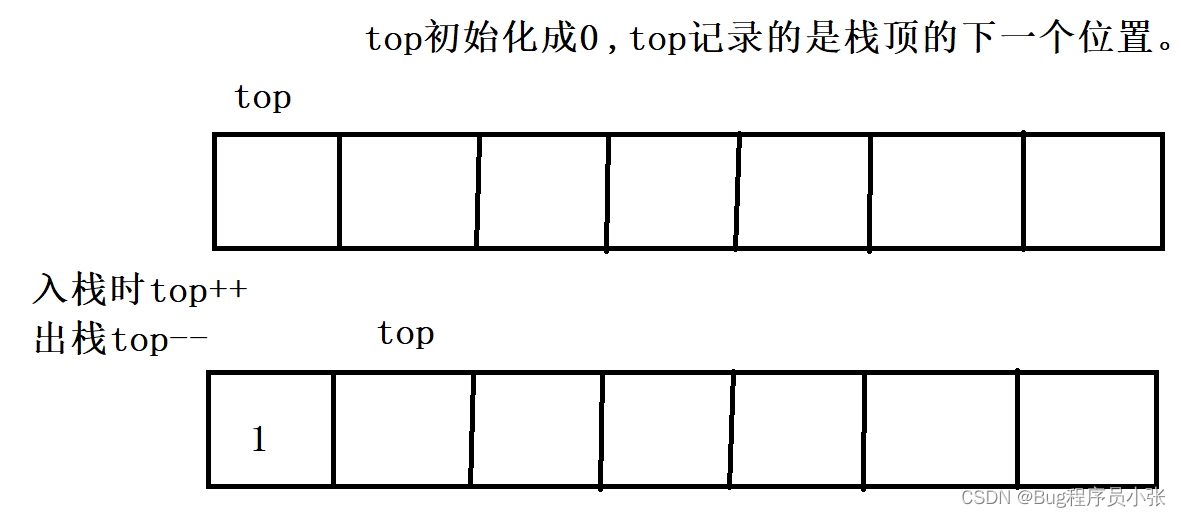
初始化栈：初始化空间的大小为4，容量为4，top记录栈顶的下一个位置。

// 初始化栈
void StackInit(Stack* ps)
{
	assert(ps);
	Stack* tmp = (Stack*)malloc(sizeof(int)*4);
	 if (tmp == NULL)
	 {
		 perror("malloc:");
		 exit(-1);
	 }
	 ps->arr = tmp;
	ps->capacity = 4;
	ps->top = 0;
}

销毁

//销毁
void StackDestroy(Stack* ps)
{
	assert(ps);
	ps->capacity = 0;
	ps->top = 0;
	free(ps->arr);
	ps->arr = NULL;
}

判空

bool StackEmpty(Stack* ps)
{
	assert(ps);
	//top = 0时栈为空
	return ps->top == 0;
}

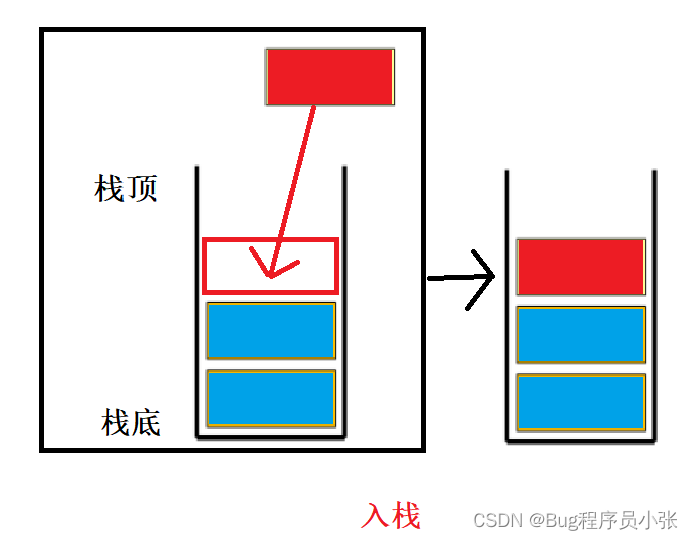
入栈

分析：入栈的时候数据插入到栈的栈顶并称为新的栈顶，初始化top的值为0,也就是说top记录的是栈顶的下一个位置，所以入栈的时候直接插入到top的位置。top++;
// 入栈
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	//判断是否需要扩容
	if (ps->top == ps->capacity)
	{
		int newcapa = ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->arr,sizeof(int)* newcapa);
		if (tmp == NULL)
		{
			perror("malloc");
			exit(-1);
		}
		ps->arr = tmp;
		ps->capacity = newcapa;
	}
	//入栈
	ps->arr[ps->top] = data;
	ps->top++;
}
入栈测试：

出栈

出栈较为简单，控制top的位置即可。
// 出栈
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}
出栈测试：出栈两次

获取栈顶元素

这里需要注意的是，栈顶元素是top的前一个位置没错。但是千万不要写成arr[--top]，这样的写法改变了top自身的值，后面的操作一定会受到影响！
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->arr[ps->top - 1];
}
测试：

获取栈中元素个数
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
	assert(ps);

	return ps->top;
}

队列

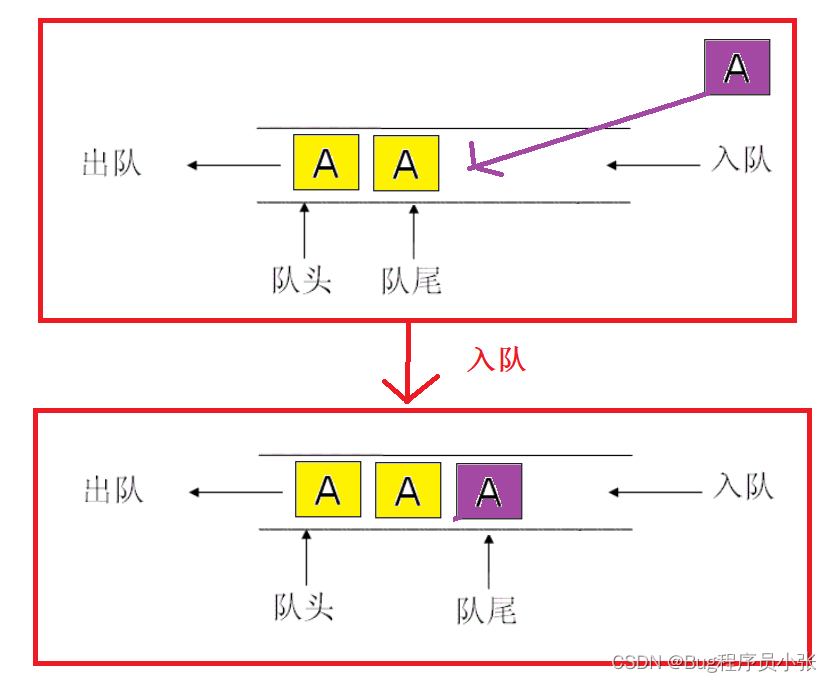
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out)

入队列：进行插入操作的一端称为队尾

出队列：进行删除操作的一端称为队头

队列可以用数组或链表的结构实现，下面的实现选用的是链表。

队列的各个接口：
//初始化
void QueueInit(Qu* q);
//销毁
void QueueDestroy(Qu* q);
//入队（尾插）
void QueuePush(Qu* q, int data);
//出队（头删）
void QeueuPop(Qu* q);
//获取头部元素
QDataType QueueFront(Qu* q);
//获取尾部元素
QDataType QueueBack(Qu* q);
//获取元素个数
int Queuesize(Qu* q);
//判断是否为NULL
bool QueueEmpty(Qu* q);
队列的在逻辑结构上就像是一个单行的管道，一边进，一边出，先进去的一定先从管道出来。正式因为这样的特性，使用链表实现队列更加的方便，入队列的时候尾插，出队列的时候头删。在单链表实现尾插的时候是遍历一次链表先找尾在插入。在这次实现队列的时候，为了方便，分别定义一个头指针和尾指针指向队列的队首和队尾。具体结构如下：
typedef int QDataType;
//表示队列
typedef struct QueueNode
{
	QDataType Val;
	struct QueueNode* next;
}QNode;
//队列结构
typedef struct Queue
{
	QNode* Head;
	QNode* Tail;
	int size;
}Qu;

初始化

//初始化
void QueueInit(Qu* q)
{
	assert(q);
	q->Head = NULL;
	q->Tail = NULL;
	q->size = 0;
}

销毁

void QueueDestroy(Qu* q)
{
	assert(q);
	QNode* cur = q->Head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	q->Head = q->Tail = NULL;
	q->size = 0;
}

检测队列是否为空

bool QueueEmpty(Qu* q)
{
	assert(q);

	return q->Head == NULL && q->Tail == NULL;
}

入队

分析：在入队的过程中，首先要申请一个节点，将这个节点入队（尾插），size++记录队中的元素个数。更新尾指针的位置。
//入队（尾插）
void QueuePush(Qu* q,int data)
{
	assert(q);
	//申请一个节点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc:");
		exit(-1);
	}
	newnode->Val = data;
	newnode->next = NULL;

	//尾插
	if (q->Tail == NULL)
	{
		q->Head = q->Tail = newnode;
	}
	else
	{
		q->Tail->next = newnode;
		q->Tail = newnode;
	}
	q->size++;
}
出队

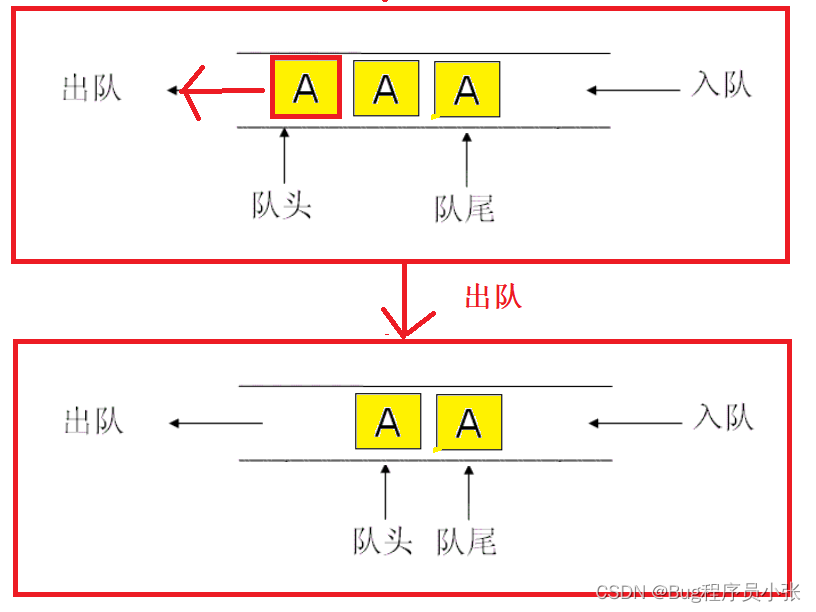
分析：出队的时候有一种较为特殊的情况，就是队列中只有一个元素，这种情况单独处理。剩下的情况正常删除，最后更新一下头指针的位置。
void QeueuPop(Qu* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	if (q->Head->next == NULL)
	{
		free(q->Head);
		q->Head = q->Tail = NULL;
	}
	else
	{
		QNode* next = q->Head->next;
		free(q->Head);
		q->Head = next;
	}
	q->size--;
}

获取队首元素

//获取头部元素
QDataType QueueFront(Qu* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->Head->Val;
}

获取队尾元素

//获取尾部元素
QDataType QueueBack(Qu* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->Tail->Val;
}

获取队列中的元素个数

int Queuesize(Qu* q)
{
	return q->size;
}

循环队列

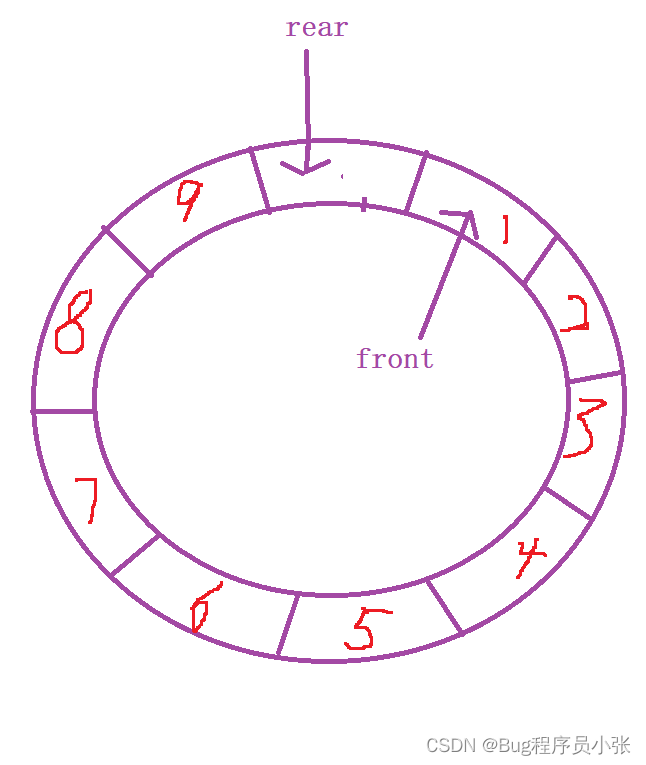
在队列的基础上，循环队里首尾相连，就像是一个圆环。

逻辑结构

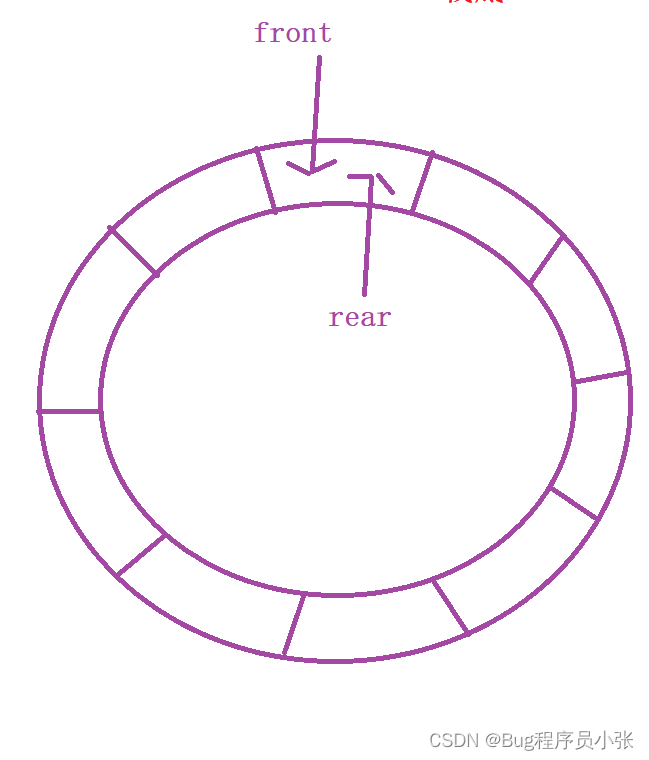
物理结构;

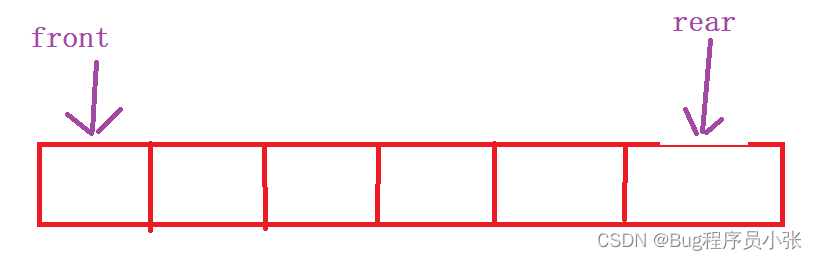
根据上面的逻辑结构，首先要考虑的问题就是什么情况队列为空，什么时候队列为满。为了解决这个问题，在存储数据的时候，留下一个空间不存储数据。

当rear == front时环形队列为空，当rear + 1 == front时，队列为满！

以OJ题为例来完成对循环队列的实现：力扣

循环队列要实现的接口：
MyCircularQueue(k): 设置队列长度为 k 。
Front: 获取队首元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。
分析：根据上图的结构，一个循环队里需要一个数组来存储数据，一个记录循环队列首部的下标，一个记录循环队列尾部的下标。还有一个记录数组能存储数据的的最大个数。

初始化时注意开辟的数组空间大小要比k多一个（原因上面分析过了）。
typedef struct 
{
    int* arr;
    int front;
    int rear;
    int sz;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    //初始化
    obj->arr = (int*)malloc(sizeof(int)*(k+1));
    obj->front = 0;
    obj->rear = 0;
    obj->sz = k;
    return obj;
}
判断队是否为空，是否为满:

这两个接口相对容易理解，根据最开始的分析，当front和rear想等的时候为空。rear+1和front想等的时候为满。但是这个思路是建立在逻辑结构上的，实际用数组实现的时候，rear+1会出现越界的问题，这个问题的解决办法：

方法1：利用数学知识取模(rear+1) % (sz+1)。sz+1是数组的最大下标元素的下一个位置。假设rear+1刚刚越界，则(rear+1) % (sz+1) = 0；

方法2：加一次判断，如果rear+1越界，也就是说rear的下一个位置下标应该回到0，判断是否和front相等。其它情况判断rear+1和front是否相等。
//检查队列是否为空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    assert(obj);
    //font和rear相等的时候为空
    return obj->front == obj->rear;
}
//检查队列是否已满
bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    assert(obj);
    //方法1：
     if(obj->rear+1 > obj->sz)
    {
        return 0 == obj->front;
    }
    else
    {
        return obj->rear+1 == obj->front;
    }
    //方法2：
    //return ((obj->rear+1)%(obj->sz+1)) == obj->front;
}
循环队列插入元素

插入元素首先要考虑的就是队列是否满了。在有空间插入的情况下，有一种特殊情况，在rear+1>sz的时候说明本次插入后rear的位置继续向后就越界了，类似于上面处理问题的方法，多判断一次，或者运用数学知识解决取模，这里不在赘述。
//插入
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    assert(obj);
    //如果队列满了不能插入数据
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    else
    {
        //插入数据
        if(obj->rear+1 > obj->sz)
        {
            obj->arr[obj->rear] = value;
            obj->rear = 0;
        }
        else
        {
            obj->arr[obj->rear++] = value;
        }
        // obj->arr[obj->rear++] = value;
        // obj->rear %= (obj->sz+1);
    }
    return true;
}
删除数据

删除数据要考虑的问题就是这个队列中海有没有数据能够删除。按照循环队列的逻辑机构front++就解决了这个问题，但是在数组实现的过程中需要特殊处理一下越界的情况，和上述方法思路相同。
//删除
bool myCircularQueueDeQueue(MyCircularQueue* obj)
{
    assert(obj);
    //如果不为空才能删除
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
     if(obj->front+1 > obj->sz)
        {
            obj->front=0;
        }
        else
        {
            obj->front++;
        }
//    obj->front++;
//    obj->front %= (obj->sz+1);
    return true;
}
返回队首、队尾元素、销毁队列
//返回队首元素
int myCircularQueueFront(MyCircularQueue* obj)
{
    assert(obj);
    //如果为空
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->arr[obj->front];
}
//返回队尾元素

int myCircularQueueRear(MyCircularQueue* obj)
{
    assert(obj);
    //如果为空
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    if(obj->rear == 0)
    {
        int rearl = obj->sz;
        return obj->arr[rearl];
    }
    else
    return obj->arr[obj->rear-1];
    //return obj->arr[(obj->rear+obj->sz)%(obj->sz+1)];
}

销毁
void myCircularQueueFree(MyCircularQueue* obj)
{
    free(obj->arr);
    free(obj);
}

OJ题

题目1：用队列实现栈

链接：力扣

分析：

首先要准备好队列的各个接口供调用！（参考上面的队列接口）

1、创建队1和队2。

2、初始化队列。

3、用队列实现入栈：

入栈实现起来的难度不是很大，队1队2的初始状态都是空，第一次入可以任意入，从第二次开始向非空队列中入数据！

4、用队列实现出栈：

出栈这里要注意一下，假设现在有一个队列和栈，数据都是1,2,3,4。按照队列先进先出的规律出队出的是1.而栈按照后进先出的逻辑出栈出的是4。所以，为了达到队列先出4的目的，将有数据队列的n-1个数据导入空队列（push）,剩下最后一个元素（size == 1）时，这就是后进来的元素，按照栈的规则它就是栈顶元素。

5、获取栈顶元素

栈顶的元素也就是有数据队列的队尾元素，在上面队列接口中提供了获取队尾元素的接口，所以这里非常方便，只需要调用下QueueBack就可以了！

6、销毁的时候除了要free(obj)，还要把队1队2释放掉

代码实现：
typedef struct {
    Qu q1;
    Qu q2;

} MyStack;


MyStack* myStackCreate() 
{
    MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
    //初始化队1、队2
    QueueInit(&(obj->q1));
    QueueInit(&(obj->q2));

    return obj;
}
//入栈
void myStackPush(MyStack* obj, int x) 
{
    //向非空队列入栈，两个都为空任意入
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}
//出栈
int myStackPop(MyStack* obj) 
{
    //确定谁是空队列
    Qu* emptyQ = &obj->q1;
    Qu* nonemptyQ = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        emptyQ = &obj->q2;
        nonemptyQ = &obj->q1;
    }
   //非空队列的数据剩下一个
    while(Queuesize(nonemptyQ)>1)
    {
         //向非空队入队数据
        QueuePush(emptyQ,QueueFront(nonemptyQ));
        printf("%d ",QueueFront(nonemptyQ));
         //出队
         QeueuPop(nonemptyQ);
    }
    //找到队尾元素
    int top = QueueFront(nonemptyQ);
    
    //出栈
   QeueuPop(nonemptyQ);

    return top;
}
//获取栈顶元素
int myStackTop(MyStack* obj)
{
    //栈顶元素相当与非空队的队尾
    if(!QueueEmpty(&(obj->q1)))
    {
        return QueueBack(&(obj->q1));
    }
    else
    {
        return QueueBack(&(obj->q2));

    }
}
//检测
bool myStackEmpty(MyStack* obj)
{
    return QueueEmpty(&(obj->q1))&& QueueEmpty(&(obj->q2));
}
//释放
void myStackFree(MyStack* obj) 
{
    QueueDestroy(&(obj->q1));
    QueueDestroy(&(obj->q2));
    free(obj);
}
题目2：用栈实现队列

链接：力扣

分析：

准备好栈的接口供调用！(参考上面的接口)

大思路：核心问题是倒数据，但是栈的特性是后进先出，倒完数据后数据的顺序和原顺序相反，也就是说区别于上一题的做法是不用倒来倒去，将入数据的栈和出数据的栈规定死，只有当出数据的栈为空时倒一下即可！

1、用栈实现入队：直接向pushst栈中入数据。

2、获取栈顶元素：直接获取popst中的栈顶数据！

3、用栈实现出队：出popst中的栈顶数据。

4、popst中没有数据了，在pushst中有数据的情况下，倒数据！

代码实现：
typedef struct 
{
    //入数据的栈，出数据的栈
    Stack Pushst;
    Stack Popst;
} MyQueue;

bool myQueueEmpty(MyQueue* obj);
int myQueuePeek(MyQueue* obj);
MyQueue* myQueueCreate() 
{
    //初始化
    MyQueue* qu = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&qu->Pushst);
    StackInit(&qu->Popst);

    return qu;
}

//入队
void myQueuePush(MyQueue* obj, int x)
{
    assert(obj);
   
    //向Pushst中入数据
    StackPush(&obj->Pushst,x);
}

int myQueuePop(MyQueue* obj)
{
    assert(obj);
    assert(!myQueueEmpty(obj));
    int top = myQueuePeek(obj);
    //出队
    StackPop(&obj->Popst);
    return top;
}

//获取栈顶元素
int myQueuePeek(MyQueue* obj)
{
    assert(obj);
    assert(!myQueueEmpty(obj));

    //如果Popst为空倒一下数据
    if(StackEmpty(&obj->Popst))
    {
       while(!StackEmpty(&obj->Pushst))
       {
            StackPush(&obj->Popst,StackTop(&obj->Pushst));
            StackPop(&obj->Pushst);
       }
    }

    return StackTop(&obj->Popst);
}

bool myQueueEmpty(MyQueue* obj)
{
    assert(obj);
    return StackEmpty(&obj->Pushst) && StackEmpty(&obj->Popst); 
}

void myQueueFree(MyQueue* obj)
{
    assert(obj);
    StackDestroy(&obj->Popst);
    StackDestroy(&obj->Pushst);
    free(obj);
}
总结：这两个题目都是围绕着队列“先进先出”，栈“后进先出”的特点实现的。核心问题都是倒数据，两个队列倒数据的时候，前后顺序不变，而栈倒完后的数据和原来的顺序相反。

题目3：循环队列