大体流程

初始化主要分成2部分，第一部分是纯视觉SfM优化滑窗内的位姿，然后在融合IMU信息。
这部分代码在estimator::processImage()最后面。

主函数入口：

void Estimator::processImage(const map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>>>> &image, const std_msgs::Header &header)

相机和imu旋转外参数的估计，分两步走：

1. 获取最新两帧之间匹配的特征点对

vector<pair<Vector3d, Vector3d>> FeatureManager::getCorresponding(int frame_count_l, int frame_count_r)

2. 计算相机-IMU之间的旋转
   利用旋转约束去估计
   $$q_{b_k{b}_{k+1}}\otimes q_{bc}=q_{bc}\otimes q_{c_k{c}_{k+1}}$$
   

bool CalibrationExRotation(vector<pair<Vector3d, Vector3d>> corres, Quaterniond delta_q_imu, Matrix3d &calib_ric_result)
{
 //! Step1: 滑窗內幀數加1
    frame_count++;
    //! Step2: 计算两帧之间的旋转矩阵
    // 利用帧可视化的3D点求解相邻两帧之间的旋转矩阵R_{ck, ck+1}
    Rc.push_back(solveRelativeR(corres)); //两帧图像之间的旋转通过solveRelativeR计算出本质矩阵E，再对矩阵进行分解得到图像帧之间的旋转R。
    //delta_q_imu为IMU预积分得到的旋转四元数，转换成矩阵形式存入Rimu当中。则Rimu中存放的是imu预积分得到的旋转矩阵
    Rimu.push_back(delta_q_imu.toRotationMatrix());
    //每帧IMU相对于起始帧IMU的R,ric初始化值为单位矩阵，则Rc_g中存入的第一个旋转向量为IMU的旋转矩阵
    Rc_g.push_back(ric.inverse() * delta_q_imu * ric);

    Eigen::MatrixXd A(frame_count * 4, 4);
    A.setZero();
    int sum_ok = 0;
    //遍历滑动窗口中的每一帧
    for (int i = 1; i <= frame_count; i++)
    {
        Quaterniond r1(Rc[i]);
        Quaterniond r2(Rc_g[i]);
        
        //！Step3:求取估计出的相机与IMU之间旋转的残差 公式(9)
        double angular_distance = 180 / M_PI * r1.angularDistance(r2);
        ROS_DEBUG(
            "%d %f", i, angular_distance);
        
        //! Step4:计算外点剔除的权重 Huber函数 公式(8) 
        double huber = angular_distance > 5.0 ? 5.0 / angular_distance : 1.0;
        ++sum_ok;
        Matrix4d L, R;
        
        //! Step5：求取系数矩阵        
        //! 得到相机对极关系得到的旋转q的左乘
        //四元数由q和w构成，q是一个三维向量，w为一个数值
        double w = Quaterniond(Rc[i]).w();
        Vector3d q = Quaterniond(Rc[i]).vec();
        //L为相机旋转四元数的左乘矩阵，Utility::skewSymmetric(q)计算的是q的反对称矩阵
        L.block<3, 3>(0, 0) = w * Matrix3d::Identity() + Utility::skewSymmetric(q);
        L.block<3, 1>(0, 3) = q;
        L.block<1, 3>(3, 0) = -q.transpose();
        L(3, 3) = w;
        
        //! 得到由IMU预积分得到的旋转q的右乘
        Quaterniond R_ij(Rimu[i]);
        w = R_ij.w();
        q = R_ij.vec();
        R.block<3, 3>(0, 0) = w * Matrix3d::Identity() - Utility::skewSymmetric(q);
        R.block<3, 1>(0, 3) = q;
        R.block<1, 3>(3, 0) = -q.transpose();
        R(3, 3) = w;

        A.block<4, 4>((i - 1) * 4, 0) = huber * (L - R);
    }
    
    //！Step6：通过SVD分解，求取相机与IMU的相对旋转    
    //！解为系数矩阵A的右奇异向量V中最小奇异值对应的特征向量
    JacobiSVD<MatrixXd> svd(A, ComputeFullU | ComputeFullV);
    Matrix<double, 4, 1> x = svd.matrixV().col(3);
    Quaterniond estimated_R(x);
    ric = estimated_R.toRotationMatrix().inverse();
    //cout << svd.singularValues().transpose() << endl;
    //cout << ric << endl;

    //！Step7：判断对于相机与IMU的相对旋转是否满足终止条件    
    //！1.用来求解相对旋转的IMU-Camera的测量对数是否大于滑窗大小。    
    //！2.A矩阵第二小的奇异值是否大于某个阈值，使A得零空间的秩为1
    Vector3d ric_cov;
    ric_cov = svd.singularValues().tail<3>();
    if (frame_count >= WINDOW_SIZE && ric_cov(1) > 0.25)
    {
        calib_ric_result = ric;
        return true;
    }
    else
        return false;
}

计算出$q_{bc}$后，对$bg$, [$v_0,v_1,...,v_n,g,s$]进行初始化

bool Estimator::initialStructure()

IMU陀螺仪bias初始化：

void solveGyroscopeBias(map<double, ImageFrame> &all_image_frame, Vector3d* Bgs)
{
    Matrix3d A;
    Vector3d b;
    Vector3d delta_bg;
    A.setZero();
    b.setZero();
    map<double, ImageFrame>::iterator frame_i;
    map<double, ImageFrame>::iterator frame_j;
    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++)
    {
        frame_j = next(frame_i);
        MatrixXd tmp_A(3, 3);
        tmp_A.setZero();
        VectorXd tmp_b(3);
        tmp_b.setZero();
        Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
        tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
        tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
        A += tmp_A.transpose() * tmp_A;
        b += tmp_A.transpose() * tmp_b;

    }
    delta_bg = A.ldlt().solve(b);
    ROS_WARN_STREAM("gyroscope bias initial calibration " << delta_bg.transpose());

    for (int i = 0; i <= WINDOW_SIZE; i++)
        Bgs[i] += delta_bg;

    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end( ); frame_i++)
    {
        frame_j = next(frame_i);
        frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
    }
}

[$v_0,v_1,...,v_n,g^{c0},s$]初始化:
$${\alpha }_{b_{k+1}}^{b_k}=R_w^{b_k}(P_{b_{k+1}}^w-P_{b_k}^w-v_{b_k}^w\Delta t+\frac{1}{2}{g}^w\Delta t^2)$$
$${\beta }_{b_{k+1}}^{b_k}=R_w^{b_k}(v_{b_{k+1}}^w-v_{b_k}^w+g^w\Delta t)$$
通过平移约束$s{p}_{b_k}^{c_0}=s{p}_{c_k}^{c_0}-R_b^{c_0}{p}_c^b$带入上式可得：
$${\alpha }_{b_{k+1}}^{b_k}=R_{c_0}^{b_k}(s(P_{b_{k+1}}^{c_0}-P_{b_k}^{c_0})-R_{b_k}^{c_0}{v}_{b_k}^{b_k}\Delta t+\frac{1}{2}{g}^{c_0}\Delta t^2)$$

$${\beta }_{b_{k+1}}^{b_k}=R_{c_0}^{b_k}(R_{b_{k+1}}^{c_0}{v}_{b_{k+1}}^{b_{k+1}}-R_{b_k}^{c_0}{v}_{b_k}^{b_k}+g^{c_0}\Delta t)$$


同样将$\delta {\beta }_{b_{k+1}}^{b_k}转为矩阵形式$

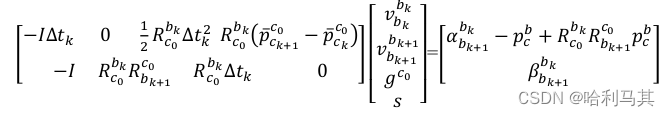
即：$H^{6\times 10}{X}_I^{10\times 1}=b^{6\times 1}$
这样，可以通过Cholosky分解下面方程求解$X_I$:
$$H_{T}H{X}_I^{10\times 1}=H^{T}b$$

bool LinearAlignment(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)
{
   int all_frame_count = all_image_frame.size();
   // 速度维度:all_frame_count * 3; 重力维度：3; scale维度:1;
   int n_state = all_frame_count * 3 + 3 + 1;

   // 构建 Ax = b 方程求解
   MatrixXd A{n_state, n_state};
   A.setZero();
   VectorXd b{n_state};
   b.setZero();

   map<double, ImageFrame>::iterator frame_i;
   map<double, ImageFrame>::iterator frame_j;
   int i = 0;
   for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
   {
       frame_j = next(frame_i);

       MatrixXd tmp_A(6, 10);
       tmp_A.setZero();
       VectorXd tmp_b(6);
       tmp_b.setZero();

       double dt = frame_j->second.pre_integration->sum_dt;

       tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
       tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();
       tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;     
       tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];
       //cout << "delta_p   " << frame_j->second.pre_integration->delta_p.transpose() << endl;
       tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
       tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
       tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();
       tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;
       //cout << "delta_v   " << frame_j->second.pre_integration->delta_v.transpose() << endl;

       Matrix<double, 6, 6> cov_inv = Matrix<double, 6, 6>::Zero();
       //cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
       //MatrixXd cov_inv = cov.inverse();
       cov_inv.setIdentity();

       MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
       VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;

       A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
       b.segment<6>(i * 3) += r_b.head<6>();

       A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
       b.tail<4>() += r_b.tail<4>();

       A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
       A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
   }
   A = A * 1000.0;
   b = b * 1000.0;
   x = A.ldlt().solve(b);
   double s = x(n_state - 1) / 100.0;
   ROS_DEBUG("estimated scale: %f", s);
   g = x.segment<3>(n_state - 4);
   ROS_DEBUG_STREAM(" result g     " << g.norm() << " " << g.transpose());
   if(fabs(g.norm() - G.norm()) > 1.0 || s < 0)
   {
       return false;
   }

   RefineGravity(all_image_frame, g, x);
   s = (x.tail<1>())(0) / 100.0;
   (x.tail<1>())(0) = s;
   ROS_DEBUG_STREAM(" refine     " << g.norm() << " " << g.transpose());
   if(s < 0.0 )
       return false;   
   else
       return true;
}