数据挖掘,计算机网络、操作系统刷题笔记40
2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开
测开的话,你就得学数据库,sql,oracle,尤其sql要学,当然,像很多金融企业、安全机构啥的,他们必须要用oracle数据库
这oracle比sql安全,强大多了,所以你需要学习,最重要的,你要是考网络警察公务员,这玩意你不会就别去报名了,耽误时间!
考网警特招必然要考操作系统,计算机网络,由于备考时间不长,你可能需要速成,我就想办法自学速成了,课程太长没法玩
刷题系列文章
【1】Oracle数据库:刷题错题本,数据库的各种概念
【2】操作系统,计算机网络,数据库刷题笔记2
【3】数据库、计算机网络,操作系统刷题笔记3
【4】数据库、计算机网络,操作系统刷题笔记4
【5】数据库、计算机网络,操作系统刷题笔记5
【6】数据库、计算机网络,操作系统刷题笔记6
【7】数据库、计算机网络,操作系统刷题笔记7
【8】数据库、计算机网络,操作系统刷题笔记8
【9】操作系统,计算机网络,数据库刷题笔记9
【10】操作系统,计算机网络,数据库刷题笔记10
【11】操作系统,计算机网络,数据库刷题笔记11
【12】操作系统,计算机网络,数据库刷题笔记12
【13】操作系统,计算机网络,数据库刷题笔记13
【14】操作系统,计算机网络,数据库刷题笔记14
【15】计算机网络、操作系统刷题笔记15
【16】数据库,计算机网络、操作系统刷题笔记16
【17】数据库,计算机网络、操作系统刷题笔记17
【18】数据库,计算机网络、操作系统刷题笔记18
【19】数据库,计算机网络、操作系统刷题笔记19
【20】数据库,计算机网络、操作系统刷题笔记20
【21】数据库,计算机网络、操作系统刷题笔记21
【22】数据库,计算机网络、操作系统刷题笔记22
【23】数据库,计算机网络、操作系统刷题笔记23
【24】数据库,计算机网络、操作系统刷题笔记24
【25】数据库,计算机网络、操作系统刷题笔记25
【26】数据库,计算机网络、操作系统刷题笔记26
【27】数据库,计算机网络、操作系统刷题笔记27
【28】数据库,计算机网络、操作系统刷题笔记28
【29】数据库,计算机网络、操作系统刷题笔记29
【30】数据库,计算机网络、操作系统刷题笔记30
【31】数据库,计算机网络、操作系统刷题笔记31
【32】数据库,计算机网络、操作系统刷题笔记32
【33】数据库,计算机网络、操作系统刷题笔记33
【34】数据库,计算机网络、操作系统刷题笔记34
【35】数据挖掘,计算机网络、操作系统刷题笔记35
【36】数据挖掘,计算机网络、操作系统刷题笔记36
【37】数据挖掘,计算机网络、操作系统刷题笔记37
【38】数据挖掘,计算机网络、操作系统刷题笔记38
【39】数据挖掘,计算机网络、操作系统刷题笔记39
文章目录
- 数据挖掘,计算机网络、操作系统刷题笔记40
- @[TOC](文章目录)
- 数据挖掘:分组与钻去
- 相关分析:斯皮尔曼相关系数
- 因子分析(成分分析)
- 本章小结
- GET是不带实体内容的,参数在请求行中,HTTP中一些请求头和实体内容是可选的。
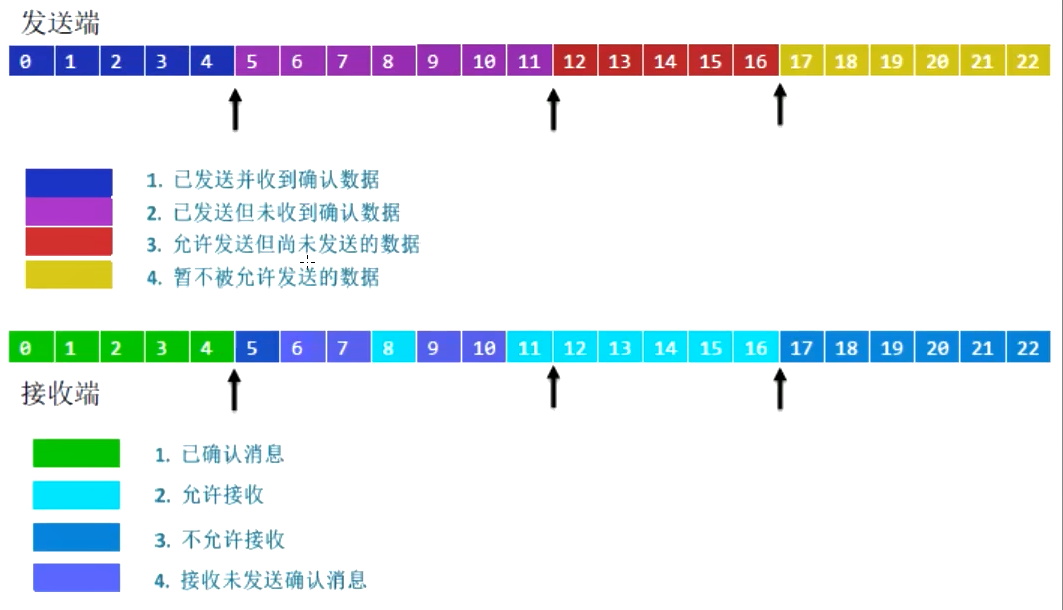
- TCP使用滑动窗口进行流量控制,流量控制实际上是对( )的控制。
- OSPF(开放的最短路径优先)采用的度量是 ________。
- Internet采用的7层OSI模型主要层次结构有?
- 默认c类是255.255.255.0 现在划分了子网掩码255.255.255.192,借了2位。 子网个数 2^2-2=2 子网的主机数 2的6-2次方 =62 62*2=124
- ADSL属于DSL技术的一种,非对称数字用户环路,上行下行速率不同,用现有电话线,不需重新布线,互相之间不干扰
- 交换机特性,找不到MAC对应,会转发到其他端口,因为有水平分割,所以不会发给发来的端口
- 以太网卡的工作模式有哪几种?
- 个计算机系统中有成千上万个文件,为了便于对文件进行存取和管理,计算机系统建立文件的索引,即文件名和文件物理位置之间的映射关系,这种文件的索引称为文件目录。
- 如果将固定块大小的文件系统中的块大小设置大一些,会造成()。
- 下列关于虚拟存储器和虚拟存储技术的描述中,错误的是() 。
- 一个进程从执行状态转换到阻塞状态的可能原因是本进程()。
- 两个合作进程,无法利用()传递信息
- 画图”程序制作的图是 __________ 。
- 被抢占进程的运行环境,即所有CPU寄存器、页表都会保存起来,因此上一个进程的执行结果不会丢失。在之前被抢占的进程恢复执行时,其进程环境可以完全恢复。
- 在历史上先后出现五种交换架构
- 只有数据帧中的目的地址与主机的地址一致时,才主机才接收这个数据帧。这里所提到的地址是( )
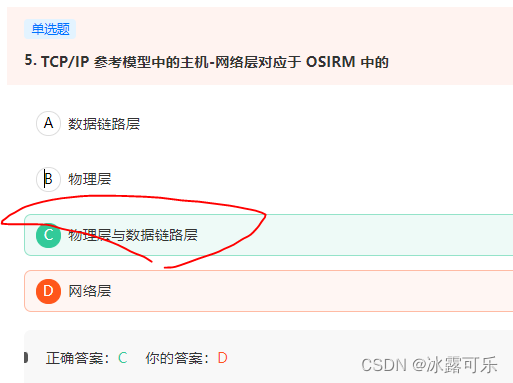
- 署队长的私人电脑可以查看到的同事的电脑,也成功了登录了QQ,但无法访问到公司的站点
- TCP/IP 参考模型中的主机-网络层对应于 OSIRM 中的
- 若要将计算机与局域网连接,至少需要具有的硬件是 ( ) 。
- 当我们在局域网内使用ping www.360.com时,哪种协议没有被使用?
- 下面列出的选项中,属于可剥夺性资源的有()
- 在下面关于虚拟存储器的叙述中,正确的是( )。
- 对于普通的计算机,对以下事件的平均耗时从小到大排序为____:
- 以下关于进程、线程、协程的的说法正确的是?
- 以下关于缓冲的说法,错误的是( )
- 磁盘高速缓存是指硬盘上集成了高速缓存的芯片,可以说是内存,提高硬盘的运行速度。
- 在Windows XP中,文件夹中可以包含文件也可以包含文件夹
- 总结
文章目录
- 数据挖掘,计算机网络、操作系统刷题笔记40
- @[TOC](文章目录)
- 数据挖掘:分组与钻去
- 相关分析:斯皮尔曼相关系数
- 因子分析(成分分析)
- 本章小结
- GET是不带实体内容的,参数在请求行中,HTTP中一些请求头和实体内容是可选的。
- TCP使用滑动窗口进行流量控制,流量控制实际上是对( )的控制。
- OSPF(开放的最短路径优先)采用的度量是 ________。
- Internet采用的7层OSI模型主要层次结构有?
- 默认c类是255.255.255.0 现在划分了子网掩码255.255.255.192,借了2位。 子网个数 2^2-2=2 子网的主机数 2的6-2次方 =62 62*2=124
- ADSL属于DSL技术的一种,非对称数字用户环路,上行下行速率不同,用现有电话线,不需重新布线,互相之间不干扰
- 交换机特性,找不到MAC对应,会转发到其他端口,因为有水平分割,所以不会发给发来的端口
- 以太网卡的工作模式有哪几种?
- 个计算机系统中有成千上万个文件,为了便于对文件进行存取和管理,计算机系统建立文件的索引,即文件名和文件物理位置之间的映射关系,这种文件的索引称为文件目录。
- 如果将固定块大小的文件系统中的块大小设置大一些,会造成()。
- 下列关于虚拟存储器和虚拟存储技术的描述中,错误的是() 。
- 一个进程从执行状态转换到阻塞状态的可能原因是本进程()。
- 两个合作进程,无法利用()传递信息
- 画图”程序制作的图是 __________ 。
- 被抢占进程的运行环境,即所有CPU寄存器、页表都会保存起来,因此上一个进程的执行结果不会丢失。在之前被抢占的进程恢复执行时,其进程环境可以完全恢复。
- 在历史上先后出现五种交换架构
- 只有数据帧中的目的地址与主机的地址一致时,才主机才接收这个数据帧。这里所提到的地址是( )
- 署队长的私人电脑可以查看到的同事的电脑,也成功了登录了QQ,但无法访问到公司的站点
- TCP/IP 参考模型中的主机-网络层对应于 OSIRM 中的
- 若要将计算机与局域网连接,至少需要具有的硬件是 ( ) 。
- 当我们在局域网内使用ping www.360.com时,哪种协议没有被使用?
- 下面列出的选项中,属于可剥夺性资源的有()
- 在下面关于虚拟存储器的叙述中,正确的是( )。
- 对于普通的计算机,对以下事件的平均耗时从小到大排序为____:
- 以下关于进程、线程、协程的的说法正确的是?
- 以下关于缓冲的说法,错误的是( )
- 磁盘高速缓存是指硬盘上集成了高速缓存的芯片,可以说是内存,提高硬盘的运行速度。
- 在Windows XP中,文件夹中可以包含文件也可以包含文件夹
- 总结
数据挖掘:分组与钻去

离散的很容易
连续的需要离散化

分组,类似于聚类
组内聚合
组间分离

标注是y1时,x1有2个,x2有1个
这叫条件count

看见了吗
标注为y1,和y2时
x1和x2分别的个数
然后做统计
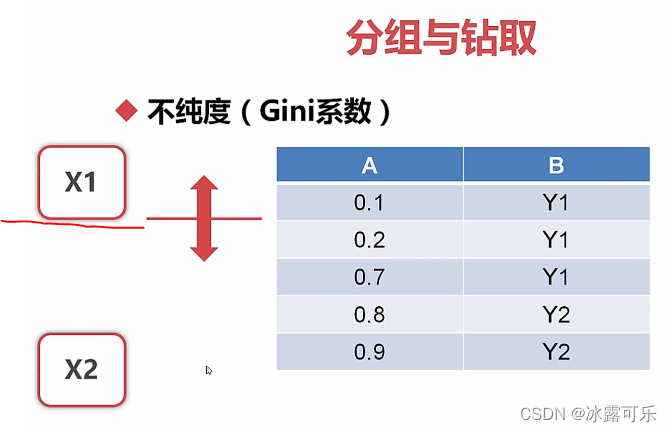


按照不同的间隔划分x1和x2的区间
找基尼系数最小的那个间隔
比如
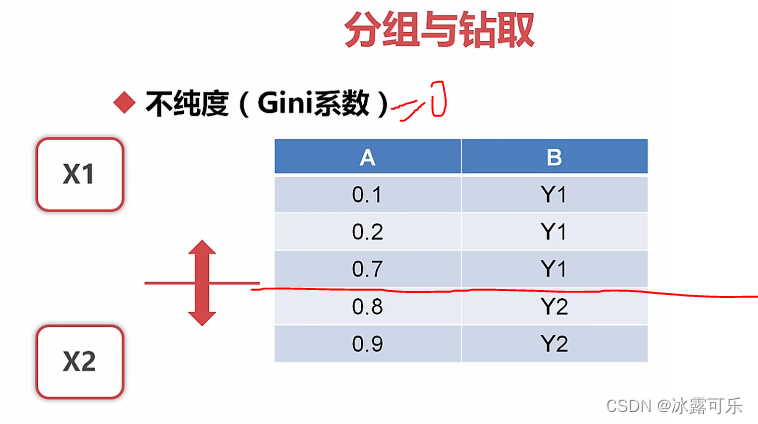
CART算法就是这么玩的
我们代码演示
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context(font_scale=1.5)
df = pd.read_csv('HR_comma_sep.csv')
def f1():
# 分组和钻取
sns.barplot(x='salary', y='left', hue='department', data=df)
plt.show()
if __name__ == '__main__':
f1()
hue拿不同的部门做分区
画left关于薪水的的分组图
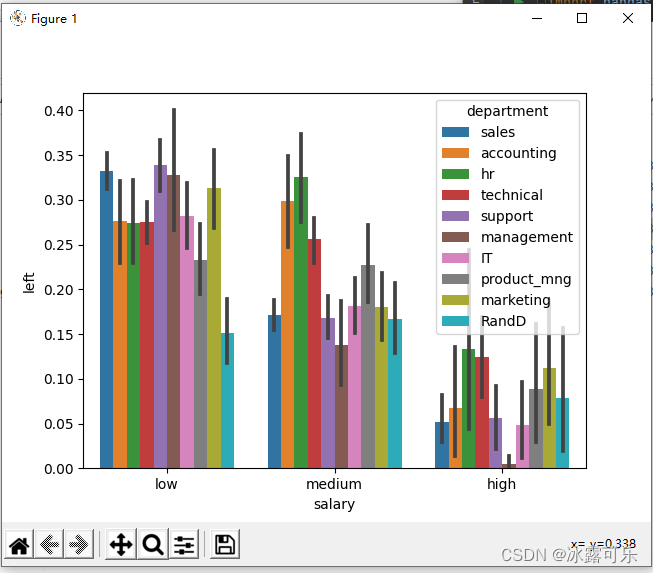
薪水整体上升的同时,离职率整体下降
但看中等薪水中
HR离职率高于管理的离职率
这些都是一图可以说明的问题
再看看连续纸
满意度
sl_s = df['satisfaction_level'] # 换
sns.barplot(x=list(range(len(sl_s))), y=sl_s.sort_values()) # 直接画x和y
# 分组默认用这些连续值
plt.show()
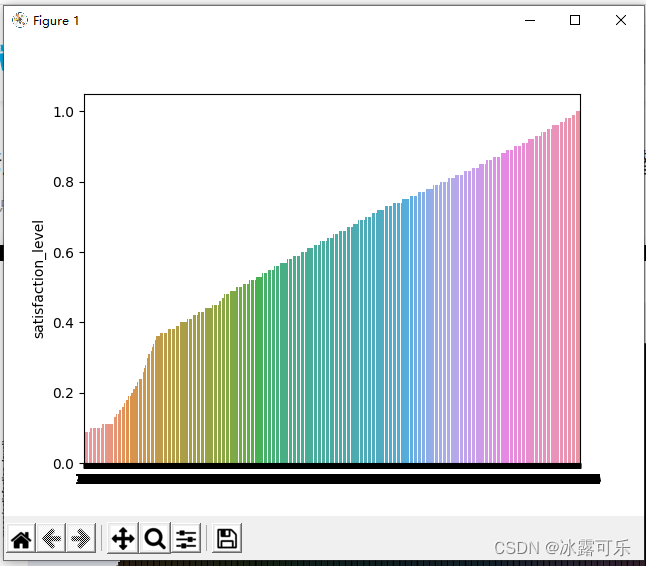
你看看,咱们的满意度,有这些取值,分组默认按照连续值看
相关分析:斯皮尔曼相关系数

我们直接把数据表.corr()打印出来
它统计了不同连续字段之间的相关性
def f2():
# 相关分析
sns.heatmap(df.corr(), vmin=-1, vmax=1, cmap=sns.color_palette('RdBu', n_colors=128))
# 没有离散属性,只看不同连续字段的相关性
# 蓝色代表1,红色接近-1,
plt.show()
if __name__ == '__main__':
f2()

离职率跟满意度是负相关,
括号那仨往往是正相关
因为工程数量多,加班就得多,这不废话吗
当然是正相关了
离散数据的那些字段的相关性呢?
二类01可以通过皮尔森相关系数来算
但是多类就难
有序的 1 2 3等级编码可以
但是无序难
最好是用熵来衡量其不确定性

其概率×log(其概率)
熵=0,说明不确定小,确定了
熵大,不确定性大
log底数为2,单位就是bit
分布是0 1,熵就是0
分布是1/2,1/2,熵就很大
条件熵,x条件小,y的熵
互信息
y的不确定
x条件下,y的不确定
有了条件的话,熵肯定减少了,这叫信息增益
I小于H
定义一个熵的增益率

然后定义一个相关性
corr(xy),下面xy对称
看例子
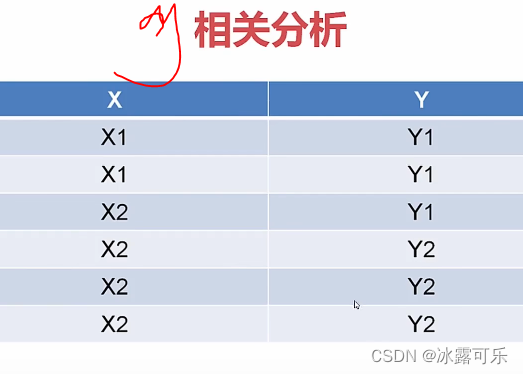
如何求熵H呢?
def f3():
# 相关分析
# 定义数组
s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
s2 = pd.Series(['y1', 'y1', 'y1', 'x2', 'x2', 'x2'])
print(getEntropy(s1))
def getEntropy(s):
# 计算分布
prt_ary = s.groupby(by=s).count().values / float(len(s)) # 自己的数量/整体的数量
return (prt_ary * (-(np.log2(prt_ary)))).sum() # 先算熵,再求和
if __name__ == '__main__':
f3()
0.9182958340544896
Process finished with exit code 0
这样就妥了
然后你看看怎么求互信息I
你得知道熵和条件熵H(X|Y)
现在x=s1,y=s2
条件熵就是知道在s1条件下,s2的熵
s1因为有很多取值,对应s2取值也不同,就要分开计算
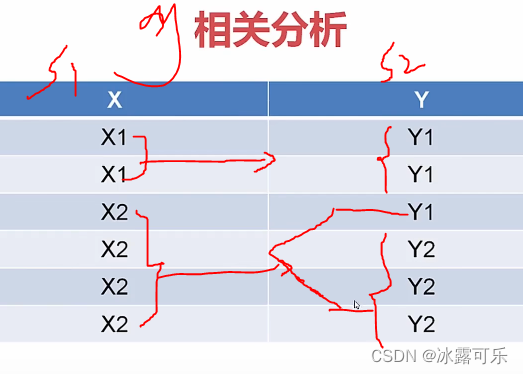
条件熵的计算公式

def getConfidentEntropy(s1, s2):
d = dict() # 定义字典,key:s1取值是xi时,value:把y1,y2组装成数组
# 比如s1是x1的条件下,把y1,y2组装成数组
# 比如s1是x2的条件下,把y1,y2组装成数组
# s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
# s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# 比如:d(x1)对应的value是[y1,y1]
# 比如:d(x2)对应的value是[y1,y2,y2,y2]
for i in range(len(s1)):
# 挨个遍历s1的取值,即x1,2,3,
d[s1[i]] = d.get(s1[i], []) + [s2[i]] # 第一项是取d中已经见过的xi,+加好对应后面直接补充的意思,
# 然后条件熵求法,求和(。。。),看看公式
# 公式里面前面是p,即每个字典key的概率,×它对应的条件熵,就是d[k]这个序列的熵
return sum([(len(d[k]) / float(len(s1))) * getEntropy(d[k]) for k in d])
通过写这个代码,就能把条件熵给求出来了
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context(font_scale=1.5)
df = pd.read_csv('HR_comma_sep.csv')
def f3():
# 相关分析
# 定义数组
s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
print(getEntropy(s1))
print(getConfidentEntropy(s1, s2))
print(getConfidentEntropy(s2, s1))
def getEntropy(s):
if not isinstance(s, pd.Series):
s = pd.Series(s) # 必须搞成series
# 计算分布
prt_ary = s.groupby(by=s).count().values / float(len(s)) # 自己的数量/整体的数量
return (prt_ary * (-(np.log2(prt_ary)))).sum() # 先算熵,再求和
def getConfidentEntropy(s1, s2):
d = dict() # 定义字典,key:s1取值是xi时,value:把y1,y2组装成数组
# 比如s1是x1的条件下,把y1,y2组装成数组
# 比如s1是x2的条件下,把y1,y2组装成数组
# s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
# s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# 比如:d(x1)对应的value是[y1,y1]
# 比如:d(x2)对应的value是[y1,y2,y2,y2]
for i in range(len(s1)):
# 挨个遍历s1的取值,即x1,2,3,
d[s1[i]] = d.get(s1[i], []) + [s2[i]] # 第一项是取d中已经见过的xi,+加好对应后面直接补充的意思,
# 然后条件熵求法,求和(。。。),看看公式
# 公式里面前面是p,即每个字典key的概率,×它对应的条件熵,就是d[k]这个序列的熵
return sum([(len(d[k]) / float(len(s1))) * getEntropy(d[k]) for k in d])
if __name__ == '__main__':
f3()
```python
0.9182958340544896
0.5408520829727552
0.4591479170272448
s1对s2的条件熵不同
s2对s1的条件熵不同
这是不对称的
所以我们说corr定义需要俩的熵
OK,I互信息就好说了
```python
def f3():
# 相关分析
# 定义数组
s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
print(getEntropy(s1))
print(getConfidentEntropy(s1, s2))
print(getConfidentEntropy(s2, s1))
print(getEntropyGain(s2, s1))
print(getEntropyGain(s1, s2))
def getEntropy(s):
if not isinstance(s, pd.Series):
s = pd.Series(s) # 必须搞成series
# 计算分布
prt_ary = s.groupby(by=s).count().values / float(len(s)) # 自己的数量/整体的数量
return (prt_ary * (-(np.log2(prt_ary)))).sum() # 先算熵,再求和
def getConfidentEntropy(s1, s2):
d = dict() # 定义字典,key:s1取值是xi时,value:把y1,y2组装成数组
# 比如s1是x1的条件下,把y1,y2组装成数组
# 比如s1是x2的条件下,把y1,y2组装成数组
# s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
# s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# 比如:d(x1)对应的value是[y1,y1]
# 比如:d(x2)对应的value是[y1,y2,y2,y2]
for i in range(len(s1)):
# 挨个遍历s1的取值,即x1,2,3,
d[s1[i]] = d.get(s1[i], []) + [s2[i]] # 第一项是取d中已经见过的xi,+加好对应后面直接补充的意思,
# 然后条件熵求法,求和(。。。),看看公式
# 公式里面前面是p,即每个字典key的概率,×它对应的条件熵,就是d[k]这个序列的熵
return sum([(len(d[k]) / float(len(s1))) * getEntropy(d[k]) for k in d])
def getEntropyGain(s1, s2):
return getEntropy(s2) - getConfidentEntropy(s1, s2) # I
if __name__ == '__main__':
f3()
0.9182958340544896
0.5408520829727552
0.4591479170272448
0.4591479170272448
0.4591479170272448
I是一样的
所以corr好说了吧

def f3():
# 相关分析
# 定义数组
s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# print(getEntropy(s1))
# print(getConfidentEntropy(s1, s2))
# print(getConfidentEntropy(s2, s1))
# print(getEntropyGain(s2, s1))
# print(getEntropyGain(s1, s2))
print(getEntropyGainRatio(s1, s2))
print(getEntropyGainRatio(s2, s1))
if __name__ == '__main__':
f3()
0.4591479170272448
0.5
增益率是不对称的哦
再看相关系数corr
def f3():
# 相关分析
# 定义数组
s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# print(getEntropy(s1))
# print(getConfidentEntropy(s1, s2))
# print(getConfidentEntropy(s2, s1))
# print(getEntropyGain(s2, s1))
# print(getEntropyGain(s1, s2))
# print(getEntropyGainRatio(s1, s2))
# print(getEntropyGainRatio(s2, s1))
print(getDiscrteCorr(s2, s1))
print(getDiscrteCorr(s1, s2))
if __name__ == '__main__':
f3()
0.4791387674918639
0.4791387674918639
这就是相关系数
离散数据的相关系数
这样不管你取值是啥,离散的就能得到相关性度量,美滋滋不???
补充一个基尼系数的代码
def getProbility2(s):
if not isinstance(s, pd.Series):
s = pd.Series(s) # 必须搞成series
# 计算分布
prt_ary = s.groupby(by=s).count().values / float(len(s)) # 自己的数量/整体的数量
# 为求基尼系数
return sum(prt_ary**2) # 平方和
def getGini(s1, s2):
d = dict() # 定义字典,key:s1取值是xi时,value:把y1,y2组装成数组
# 比如s1是x1的条件下,把y1,y2组装成数组
# 比如s1是x2的条件下,把y1,y2组装成数组
# s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
# s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# 比如:d(x1)对应的value是[y1,y1]
# 比如:d(x2)对应的value是[y1,y2,y2,y2]
for i in range(len(s1)):
# 挨个遍历s1的取值,即x1,2,3,
d[s1[i]] = d.get(s1[i], []) + [s2[i]] # 第一项是取d中已经见过的xi,+加好对应后面直接补充的意思,
return 1 - sum([getProbility2(d[k]) * len(d[k]) / float(len(s1)) for k in d]) # 这是求基尼系数
def f3():
# 相关分析
# 定义数组
s1 = pd.Series(['x1', 'x1', 'x2', 'x2', 'x2', 'x2'])
s2 = pd.Series(['y1', 'y1', 'y1', 'y2', 'y2', 'y2'])
# print(getEntropy(s1))
# print(getConfidentEntropy(s1, s2))
# print(getConfidentEntropy(s2, s1))
# print(getEntropyGain(s2, s1))
# print(getEntropyGain(s1, s2))
# print(getEntropyGainRatio(s1, s2))
# print(getEntropyGainRatio(s2, s1))
# print(getDiscrteCorr(s2, s1))
# print(getDiscrteCorr(s1, s2))
print(getGini(s1, s2))
print(getGini(s2, s1))
if __name__ == '__main__':
f3()
0.25
0.2222222222222222
不对称哦
因子分析(成分分析)
探索性
协方差、降维
验证性
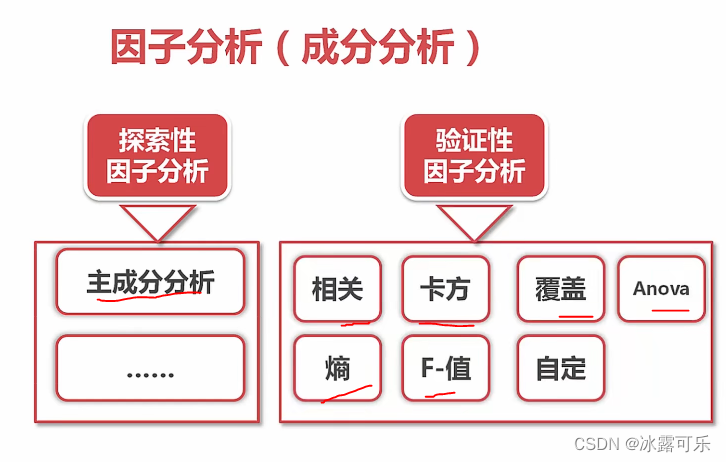

探索性
一个属性和另一个属性的关系
from sklearn.decomposition import PCA
def f4():
my_pca = PCA(n_components=7) #原始表格字段为10个字段,我们需要去掉3个
my_pca.fit_transform(df.drop(labels=['salary', 'department', 'left'], axis=1)) # 剩余字段为7个列
print(my_pca.explained_variance_ratio_)
if __name__ == '__main__':
f4()
[9.98565340e-01 8.69246970e-04 4.73865973e-04 4.96932182e-05
2.43172315e-05 9.29496619e-06 8.24128218e-06]
就第一个值大,后面的值都很小
说明主成分因子只剩一个了
看看相关图
from sklearn.decomposition import PCA
def f4():
my_pca = PCA(n_components=7) #原始表格字段为10个字段,我们需要去掉3个
lower_mat = my_pca.fit_transform(df.drop(labels=['salary', 'department', 'left'], axis=1)) # 剩余字段为7个列
print(my_pca.explained_variance_ratio_)
data = pd.DataFrame(lower_mat)
sns.heatmap(data=data.corr(), vmin=-1, vmax=1, cmap=sns.color_palette('RdBu', n_colors=128)) # 热力图
plt.show()
if __name__ == '__main__':
f4()
利用pca降维之后,只有一个维度有效,那就是彻底降维区分开了

只有对角线相关性才为1,
原始的特征空间直接降维成正交的特征空间
懂了吧?
本章小结

GET是不带实体内容的,参数在请求行中,HTTP中一些请求头和实体内容是可选的。

TCP使用滑动窗口进行流量控制,流量控制实际上是对( )的控制。

OSPF(开放的最短路径优先)采用的度量是 ________。

Internet采用的7层OSI模型主要层次结构有?
多选
齐了才行
骚
默认c类是255.255.255.0 现在划分了子网掩码255.255.255.192,借了2位。 子网个数 2^2-2=2 子网的主机数 2的6-2次方 =62 62*2=124
主机位00也不能用的
网络位11也不能用???
骚啊
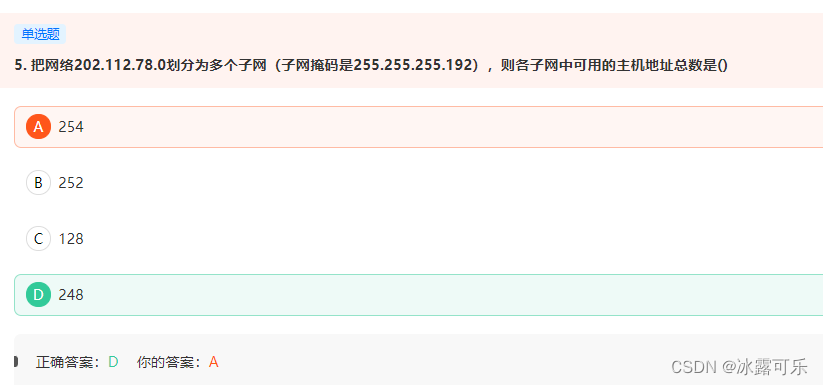
不,就是能用啊
我的A是对的
操
ADSL属于DSL技术的一种,非对称数字用户环路,上行下行速率不同,用现有电话线,不需重新布线,互相之间不干扰
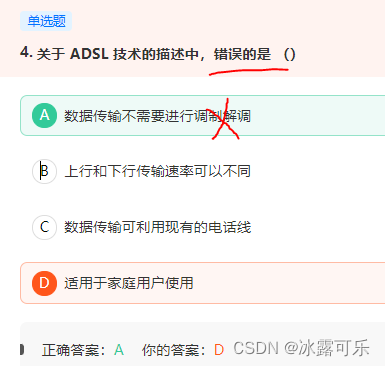
任何信号都需要调制解调
最基本的技术
交换机特性,找不到MAC对应,会转发到其他端口,因为有水平分割,所以不会发给发来的端口

以太网卡的工作模式有哪几种?

个计算机系统中有成千上万个文件,为了便于对文件进行存取和管理,计算机系统建立文件的索引,即文件名和文件物理位置之间的映射关系,这种文件的索引称为文件目录。

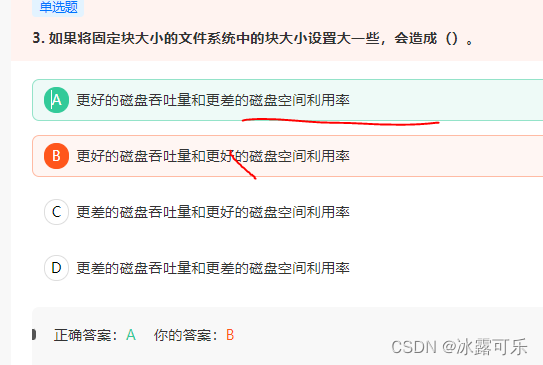
如果将固定块大小的文件系统中的块大小设置大一些,会造成()。
想的是这个答案,但是选错了
下列关于虚拟存储器和虚拟存储技术的描述中,错误的是() 。
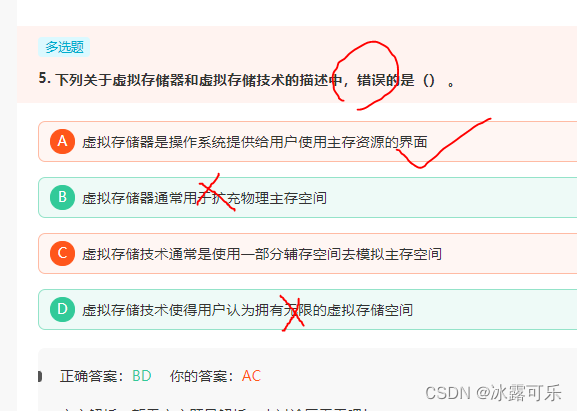
审题知道是错误,但是选择搞正确的了
态度不认真
一个进程从执行状态转换到阻塞状态的可能原因是本进程()。

V是释放了cpu有资源了,咋还阻塞呢
你说
两个合作进程,无法利用()传递信息
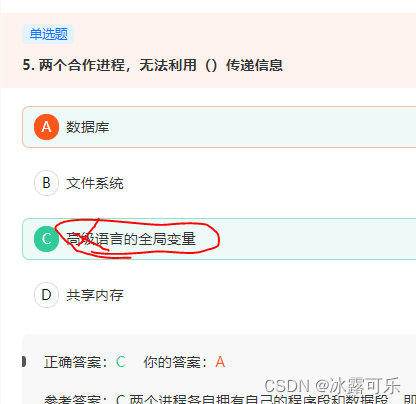
应该是原语
高级语言不行
画图”程序制作的图是 __________ 。

被抢占进程的运行环境,即所有CPU寄存器、页表都会保存起来,因此上一个进程的执行结果不会丢失。在之前被抢占的进程恢复执行时,其进程环境可以完全恢复。
自己的东西保存好,大家的东西你别动
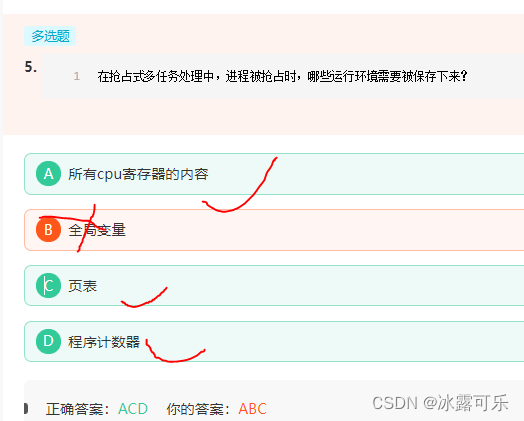
在历史上先后出现五种交换架构
链接:https://www.nowcoder.com/questionTerminal/d13d46bca07749508f04d8857ca7711d
来源:牛客网
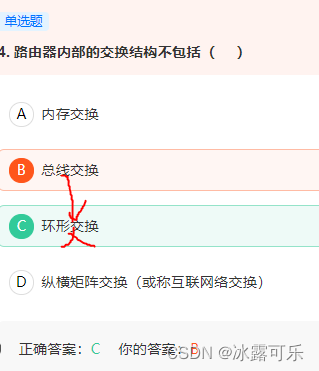
在历史上先后出现五种交换架构,包括:
1. 共享总线交换
**2. 环型总线交换:**实质上仍然是一种总线交换,相对于共享总线交换,其将总线移到线卡的芯片中,而不是在背板上,交换带宽有所提高,但是没有本质的改善。
3. 共享内存交换
4. Crossbar矩阵交换
5. 基于动态路由的CLOS多级交换。
只有数据帧中的目的地址与主机的地址一致时,才主机才接收这个数据帧。这里所提到的地址是( )
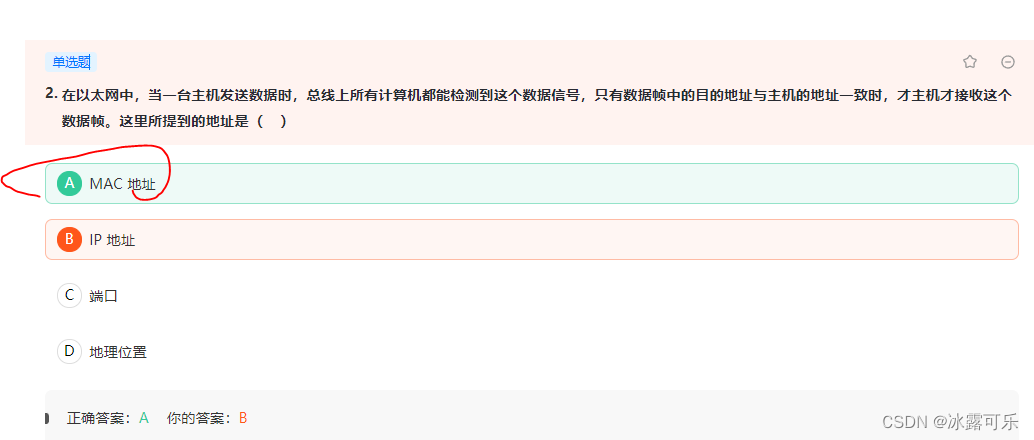
署队长的私人电脑可以查看到的同事的电脑,也成功了登录了QQ,但无法访问到公司的站点
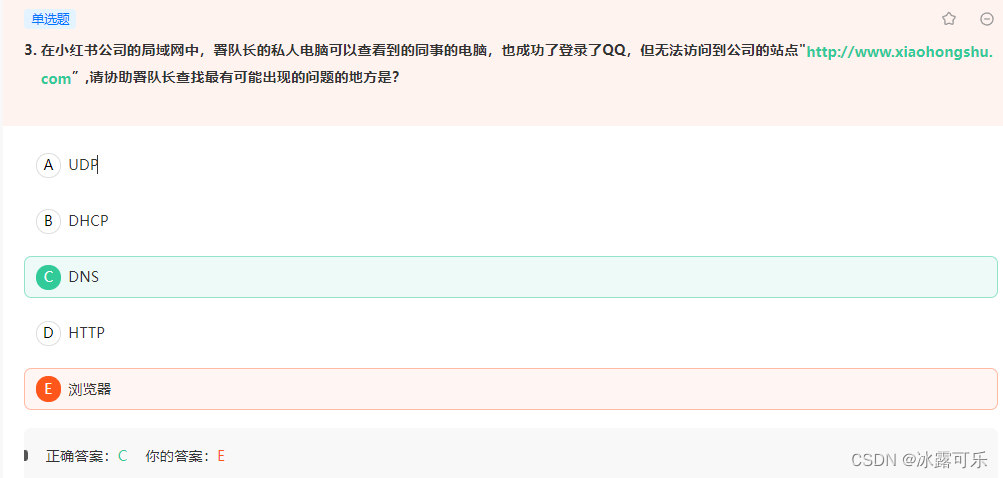
TCP/IP 参考模型中的主机-网络层对应于 OSIRM 中的
若要将计算机与局域网连接,至少需要具有的硬件是 ( ) 。

当我们在局域网内使用ping www.360.com时,哪种协议没有被使用?

下面列出的选项中,属于可剥夺性资源的有()
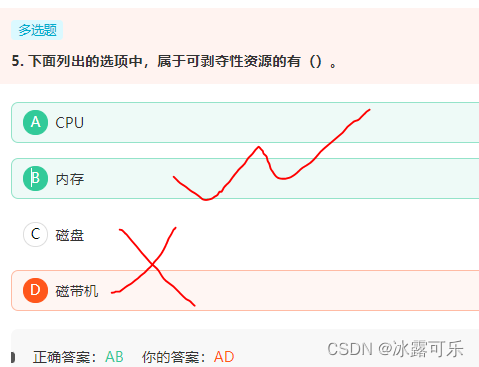
链接:https://www.nowcoder.com/questionTerminal/d7375249214648c6b3b12ce8184efea2
来源:牛客网
系统中的资源可以分为两类,
一类是可剥夺资源,是指某进程在获得这类资源后,该资源可以再被其他进程或系统剥夺。
例如,优先权高的进程可以剥夺优先权低的进程的 处理机 。
又如,内存区可由 存储器管理 程序,把一个进程从一个存储区移到另一个存储区,此即剥夺了该进程原来占有的存储区,甚至可将一进程从内存调到外存上,可见, CPU 和 主存 均属于可剥夺性资源。
另一类资源是不可剥夺资源,当系统把这类资源分配给某进程后,再不能强行收回,只能在进程用完后自行释放,如 磁带机 、打印机等
在下面关于虚拟存储器的叙述中,正确的是( )。
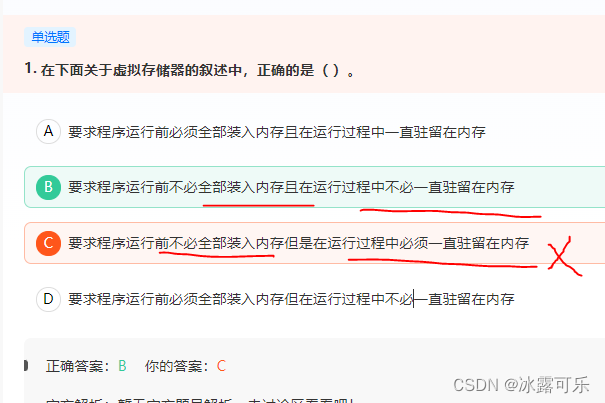
运行时快速调换
对于普通的计算机,对以下事件的平均耗时从小到大排序为____:
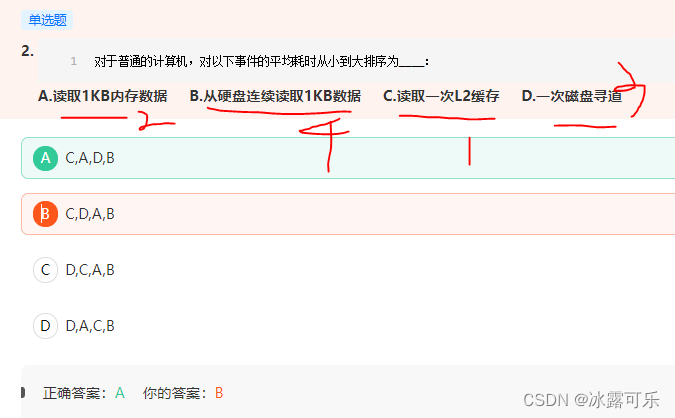
以下关于进程、线程、协程的的说法正确的是?
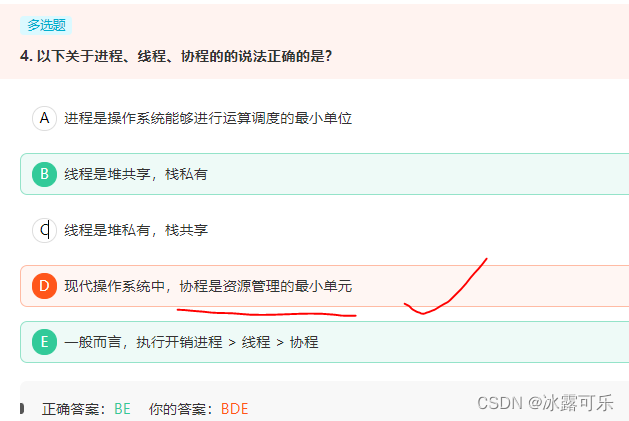
以下关于缓冲的说法,错误的是( )
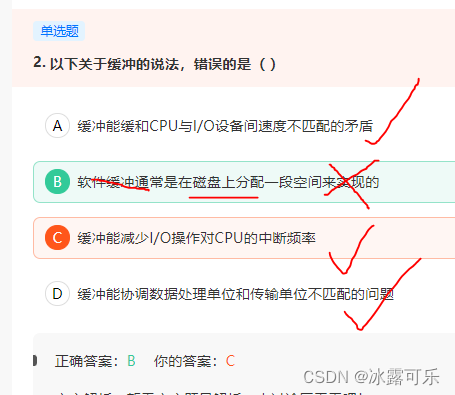
磁盘高速缓存是指硬盘上集成了高速缓存的芯片,可以说是内存,提高硬盘的运行速度。

在Windows XP中,文件夹中可以包含文件也可以包含文件夹

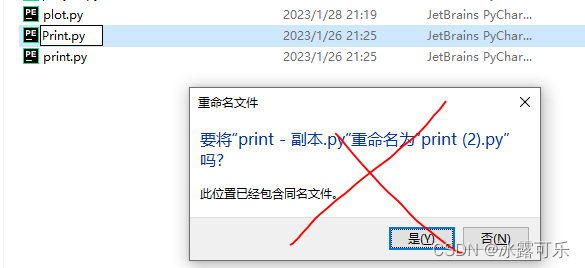
C怎么说,操蛋
就是不区分啊
之前就有一个题就是这样说的
总结
提示:重要经验:
1)
2)学好oracle,操作系统,计算机网络,即使经济寒冬,整个测开offer绝对不是问题!同时也是你考公网络警察的必经之路。
3)笔试求AC,可以不考虑空间复杂度,但是面试既要考虑时间复杂度最优,也要考虑空间复杂度最优。