数组及特殊矩阵
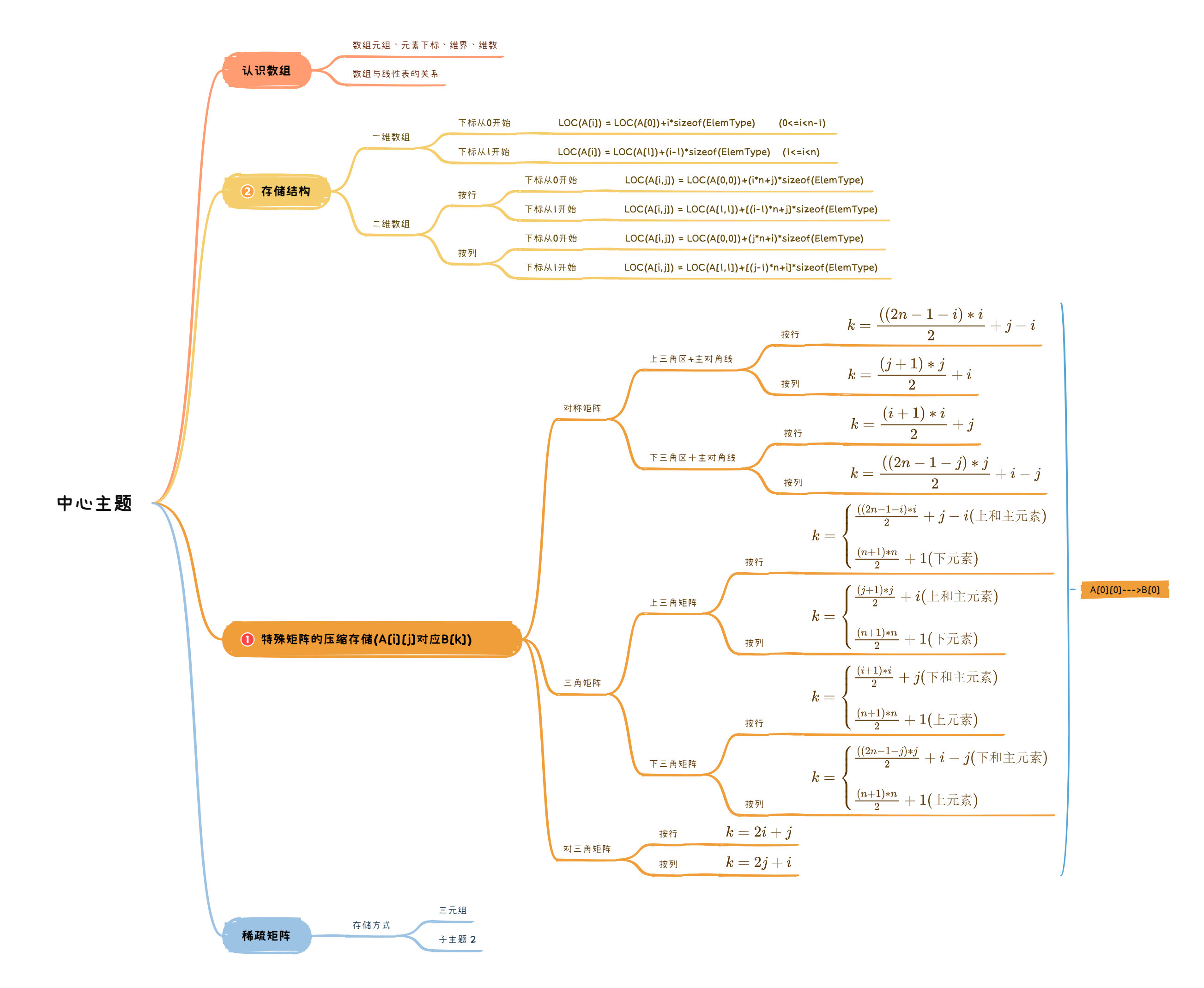
- 一、认识数组
- 1️⃣ 定义
- 2️⃣ 存储结构
- 1. 一维数组
- 2. 二维数组
- 二、特殊矩阵的压缩存储
- 1️⃣ 对称矩阵
- 💤思考1:有多少个二维元素`A[0...n-1][0...n-1]`存于一维元素中❓
- 💤思考2:按行排列,二维数组A[0...n-1][0...n-1]与一维数组B[0... ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n} 2-1 2(n+1)∗n−1]对应的关系❓
- 💤思考3:按列排列,二维数组A[0...n-1][0...n-1]与一维数组B[0... ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n } 2-1 2(n+1)∗n−1]对应的关系❓
- 💤思考4:思考二、三都是以下三角区为例,那么上三角区如何存储❓
- 2️⃣ 三角矩阵
- 💤思考5:有多少个二维元素`A[0...n-1][0...n-1]`存于一维元素中❓
- 💤思考6:下三角矩阵如何存储❓
- 💤思考7:上三角矩阵如何存储❓
- 3️⃣三对角矩阵
- 💤思考8:有多少个二维元素`A[0...n-1][0...n-1]`存于一维元素中❓
- 💤思考9:按行排序,二维数组`A[0...n-1][0...n-1]`与一维数组`B[0...3n-3]`对应的关系❓
- 💤思考10:按列排序,二维数组`A[0...n-1][0...n-1]`与一维数组`B[0...3n-3]`对应的关系❓
- 三、稀疏矩阵
- 参考资料

一、认识数组
1️⃣ 定义
-
什么是数组❓
数组是由 n ( n ⩾ 1 ) n(n\geqslant1) n(n⩾1)个相同类型的数据元素的有限序列。
除了定义还需认识一些知识点:
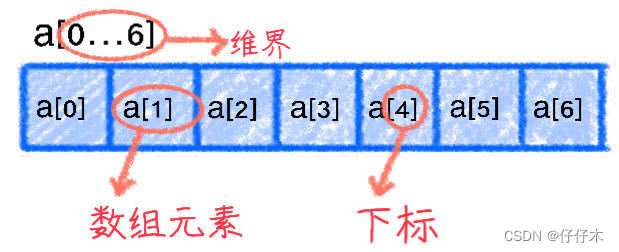
- 💡数组元素:数组中的每个数据元素称为一个数组元素。
- 💡元素下标:每个元素中的序号
- 💡维界:下标的取值范围(例:下图0…6为该数组维界)
- 💡维数:a[7]: 一维数组、a[2][2]:二维数组、a[1][2][3]:三维数组
- 💡 各数组元素大小相同(数据类型相同,字长相同,即大小相同),且物理上连续存放
-
👀数组与线性表的关系
- 数组是线性表的推广。一维数组可以视为一个线形表;二维数组可视为其元素也是定长线性表的线性表。
- 数组一旦被定义,其维数和维界就不在改变。因此,除结构的初始化和销毁外,数组只会有存取元素和修改元素的操作。
2️⃣ 存储结构
由于数组在物理上是连续存储的,所以只要知道数组的起始地址、数据类型,就可以算出其存储位置
1. 一维数组
若一维数组A[n],则其存储结构关系式为:
数组下标从0开始:LOC(A[i]) = LOC(A[0])+i*sizeof(ElemType) (0<=i<n-1)
数组下标从1开始:LOC(A[i]) = LOC(A[1])+(i-1)*sizeof(ElemType) (1<=i<n)
🐂小试牛刀
📋题目描述:
一维数组A[0...n]采用顺序存储结构,每个元素占用4个字节,该数组的首地址为120,求A[4]的存储地址( )
✅正确答案:136
👻题目解析:
注意数组下标是从0开始的
如图:
💡第一个4:0—4之间一共有四个元素
💡第二个4:该数组是int类型,字节为4B
2. 二维数组
对于多维数组,有两种映射方法:按行优先、按列优先
-
按行存储
📌基本思想:
先行后列,先存储行号比较小的元素,行号相等先存储列号比较小的元素。设二维数组
A[m][n],则存储结构关系式为:数组下标从0开始:LOC(A[i,j]) = LOC(A[0,0])+(i*n+j)*sizeof(ElemType) 数组下标从1开始:LOC(A[i,j]) = LOC(A[1,1])+[(i-1)*n+j]*sizeof(ElemType)🐂小试牛刀
📋题目描述:
假设二维数组A[3,4]每个元素占用2个存储单元,数组元素(A[0][0])的起始地址为1000,求数组元素A[2][2]的起始地址。
✅正确答案:1020
👻题目解析:
注意数组下标是从0开始的
公式求解:LOC(A[2,2]) = LOC(A[0,0])+(2*4+2)*2=1000+20=1020
图解:
-
-
列优先(原理同上)
📌基本思想:
先列后行,先存储列号比较小的元素,列号相等先存储行号比较小的元素。设二维数组
A[m][n],则存储结构关系式为:数组下标从0开始:LOC(A[i,j]) = LOC(A[0,0])+(j*n+i)*sizeof(ElemType) 数组下标从1开始:LOC(A[i,j]) = LOC(A[1,1])+[(j-1)*n+i]*sizeof(ElemType)
-

二、特殊矩阵的压缩存储
1.💡 压缩矩阵:指为多个值相同的元素分配一个存储空间,对零元素不分配存储空间。其目的是节省存储空间
2. 💡特殊矩阵:值具有许多相同矩阵元素或零元素,并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。常见特殊矩阵有对称矩阵、上(下)三角矩阵、对角矩阵等。
3. 💡特殊矩阵的压缩存储方法:找到特殊矩阵中值相同的矩阵元素的分布规律,把那些呈现规律性分布的、值相同的多个矩阵元素压缩到一个存储空间中。
1️⃣ 对称矩阵
-
对称矩阵是什么❓
上三角区的元素==下三角区元素,A[i][j]==A[j][i]

-
对称矩阵为何不能用二维矩阵存储❓
对于n阶对称矩阵,上三角元素的所有元素和下三角区对应的元素相同,若扔采用二维数组存放,则会浪费一半的空间,对此将对称矩阵存放在一维数组中。 -
那么如何将二维数组存储于一维数组❓
💤思考1:有多少个二维元素
A[0...n-1][0...n-1]存于一维元素中❓
由于上三角区==下三角区,只需要在一维数组中存储主对角线+下三角区

第 1 行(A[0]):1 个元素 第 2 行(A[1]):2 个元素 第 3 行(A[2]):3 个元素 ...... 第 n 行(A[n-1]):n个元素(❗由于数组从0开始,A[0]占了一行,所以A[n]是第n-1行) 共:1+2+3+...+n=[1+n]*n/2=(n+1)*n/2✅答案:一维数组共需存储 ( n + 1 ) ∗ n 2 \frac {(n+1)*n} 2 2(n+1)∗n个元素
💤思考2:按行排列,二维数组A[0…n-1][0…n-1]与一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n} 2-1 2(n+1)∗n−1]对应的关系❓
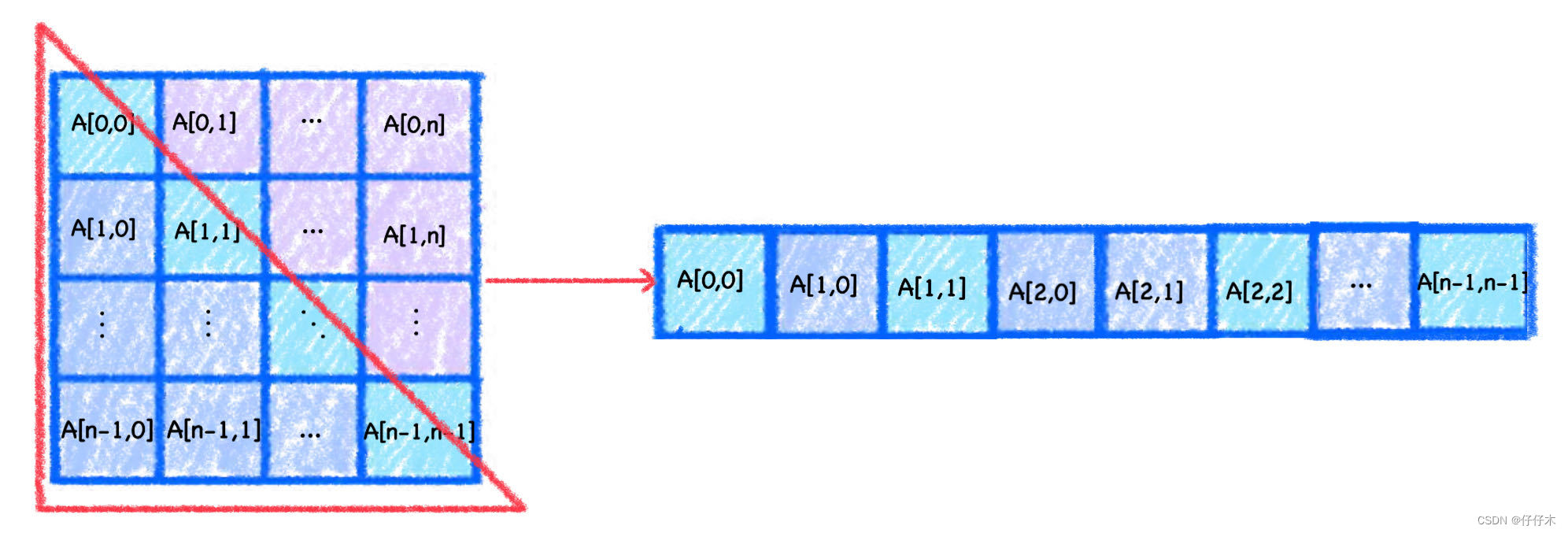
👀看图做题:- 求
A[1][1]在一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n } 2-1 2(n+1)∗n−1]的位置:A[1][1]位于第2行的第2列 第1行:共1个元素 第2行:有2个元素 求和:1+2=3 B的下标从0开始,所以3-1=2,即A[1][1]`在一维数组B[2]中 - 求
A[2][1]在一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n} 2-1 2(n+1)∗n−1]的位置:A[2][1]位于第3行的第2列 第1行:共1个元素 第2行:共2个元素 第3行:有2个元素 求和:1+2+3=5 B的下标从0开始,所以5-1=4,即A[2][1]`在一维数组B[4]中 - 求
A[i][j]在一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n } 2-1 2(n+1)∗n−1]的位置:A[i][j]位于第i+1行的第j+1列 第 1 行:共 1 个元素 第 2 行:共 2 个元素 第 3 行:共 3 个元素 ... 第 i 行:共 i 个元素 第i+1行:有j+1个元素 求和:1+2+3+...+i+(j+1)=(i+1)*i/2+(j+1) B的下标从0开始,所以(i+1)*i/2+(j+1)-1=(i+1)*i/2+j,即A[i][j]`在一维数组B[(i+1)*i/2+j]中
✅答案:按行排序,二位数组
A[i][j]与一维数组B[ ( i + 1 ) ∗ i 2 + j \frac {(i+1)*i} 2+j 2(i+1)∗i+j]对应💤思考3:按列排列,二维数组A[0…n-1][0…n-1]与一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n } 2-1 2(n+1)∗n−1]对应的关系❓
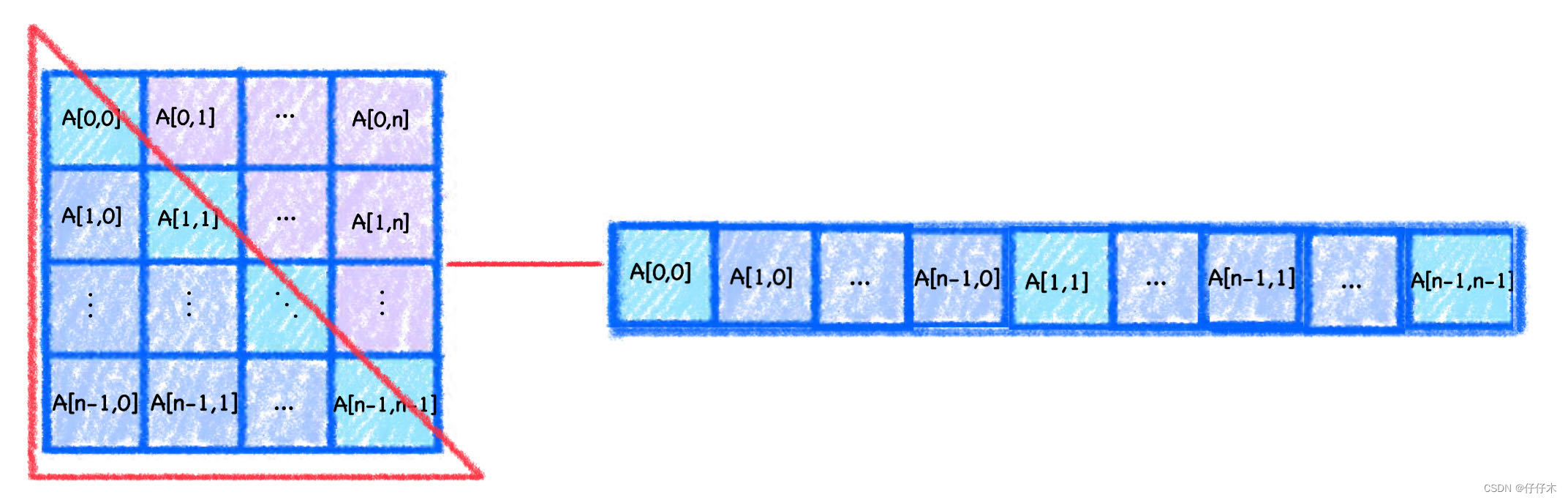
👀看图做题:- 求
A[1][1]在一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n } 2-1 2(n+1)∗n−1]的位置:A[1][1]位于第2行的第2列 第1列:共n-1个元素 第2列:有1个元素 求和:n-1+1=n B的下标从0开始,所以n-1=(n-1),即A[1][1]`在一维数组B[n-1]中 - 求
A[2][1]在一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n} 2-1 2(n+1)∗n−1]的位置:A[2][1]位于第3行的第2列 第1列:共n-1个元素 第2列:共2个元素 求和:n-1+2=n+1 B的下标从0开始,所以n+1-1=n,即A[2][1]`在一维数组B[n]中 - 求
A[i][j]在一维数组B[0… ( n + 1 ) ∗ n 2 − 1 \frac {(n+1)*n } 2-1 2(n+1)∗n−1]的位置:A[i][j]位于第i+1行的第j+1列 第 1 列:共 n-1 个元素 第 2 列:共 n-2 个元素 第 3 列:共 n-3 个元素 ... 第 j 列:共 n-j 个元素 第j+1列:有i+1-j个元素 求和:(n-1)+(n-2)+(n-3)+...+(n-j)+(i+1-j)=(n-1+n-j)*j/2+i+1-j=(2n-1-j)*j/2+i+1-j B的下标从0开始,所以(2n-1-j)*j/2+i+1-j-1=(2n-1-j)*j/2+i-j,即A[i][j]在一维数组B[(2n-1-j)*j/2+i-j]中
✅答案:按列排序,二位数组
A[i][j]与一维数组B[ ( ( 2 n − 1 − j ) ∗ j 2 + i − j \frac {((2n-1-j)*j} 2+i-j 2((2n−1−j)∗j+i−j]对应💤思考4:思考二、三都是以下三角区为例,那么上三角区如何存储❓

由图可知,上三角区与下三角区的关系为:A[i][j]==A[j][i]
所以:- 💡上按行==下按列,二位数组
A[i][j]与一维数组B[ ( ( 2 n − 1 − i ) ∗ i 2 + j − i \frac {((2n-1-i)*i} 2+j-i 2((2n−1−i)∗i+j−i]对应 - 💡上按列==上按排,二位数组
A[i][j]与一维数组B[ ( j + 1 ) ∗ j 2 + i \frac {(j+1)*j} 2+i 2(j+1)∗j+i]对应
- 求
2️⃣ 三角矩阵
-
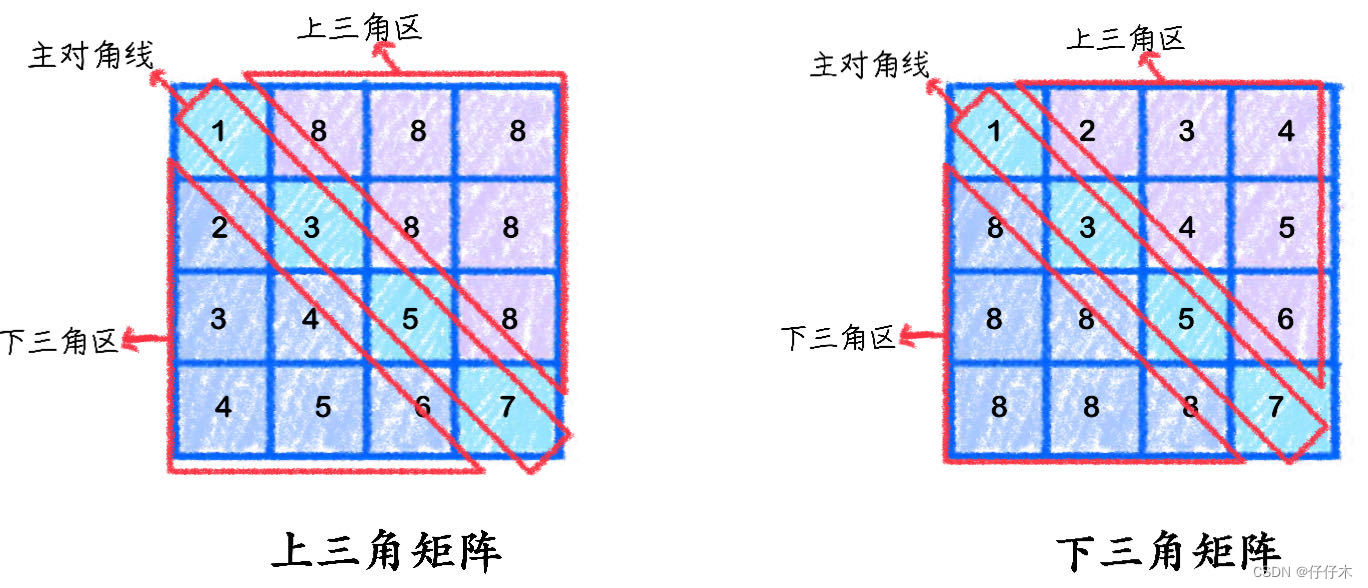
三角矩阵是什么❓
三角矩阵可以分为上三角矩阵和下三角矩阵- 💡下三角矩阵:上三角区所有元素均为一个常量
- 💡上三角矩阵:下三角区所有元素均为一个常量
-
三角矩阵如何存储❓
💤思考5:有多少个二维元素
A[0...n-1][0...n-1]存于一维元素中❓以下三角矩阵为例:
三角矩阵与对称矩阵的存储方式相似,不同之处在于,)存储完下三角区和主对角线后,紧接着存储上三角区的常量一次
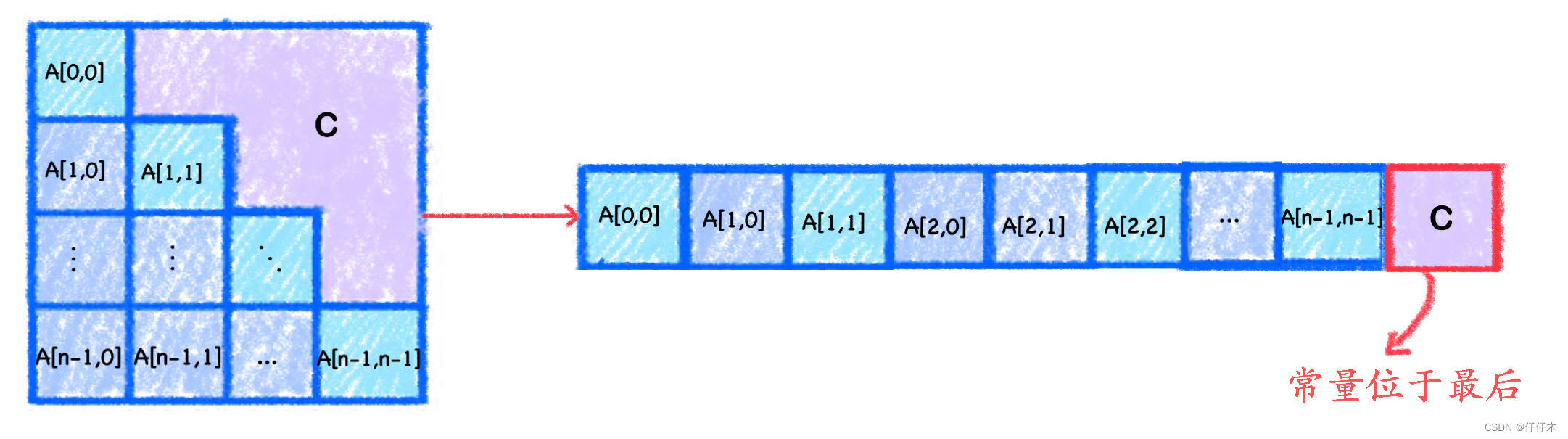
由对称矩阵可知,下三角区+主对角线的元素=(n+1)*n /2个元素 三角矩阵多了一个常量:所以共有(n+1)*n /2+1个元素✅答案:一维数组共需存储 ( n + 1 ) ∗ n 2 + 1 \frac {(n+1)*n} 2+1 2(n+1)∗n+1个元素
💤思考6:下三角矩阵如何存储❓
-
按行存储
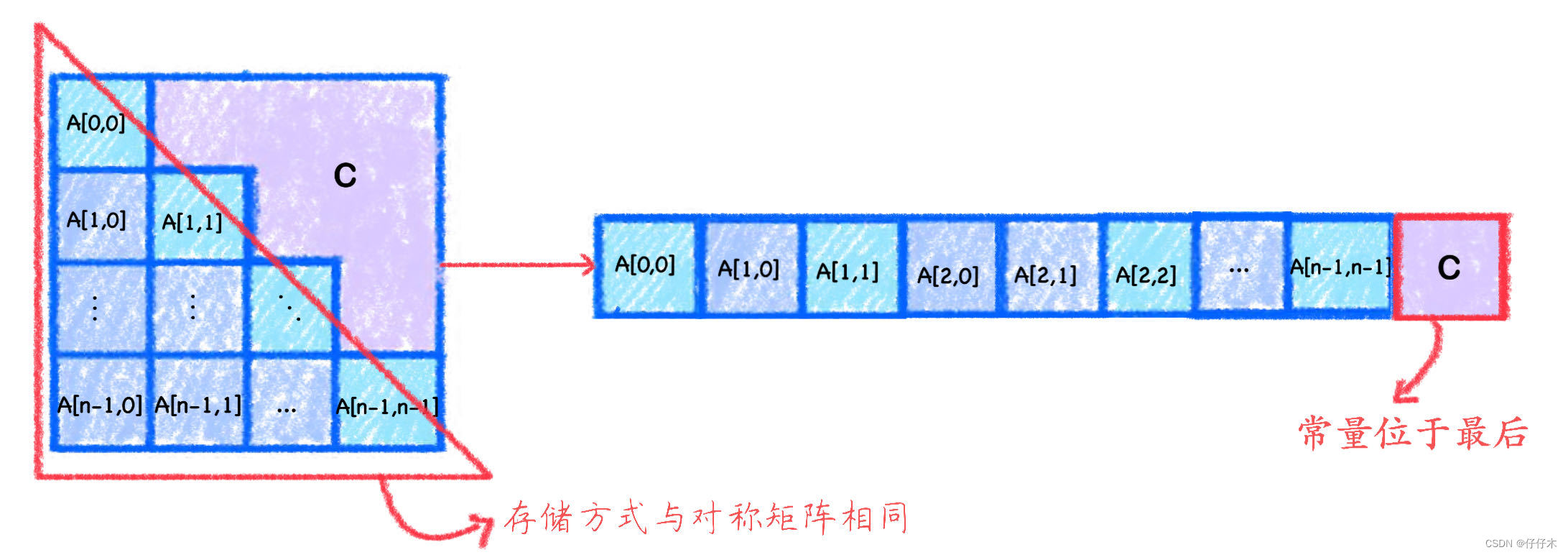
👀看图知:- 💡三角矩阵的
下三角区+主对角线与对阵矩阵存储相同,可直接使用思考二的结论. - 💡三角矩阵的
上三角区的常量存于一维数组的最后,所以位置固定: ( n + 1 ) ∗ n 2 \frac {(n+1)*n} 2 2(n+1)∗n
✅答案:按行排序,二维数组
A[i][j]与B[k]相对应,其中 k = { ( i + 1 ) ∗ i 2 + j ( 下和主元素 ) ( n + 1 ) ∗ n 2 + 1 ( 上元素 ) k= \begin{cases} {\frac {(i+1)*i} 2+j} (下和主元素) \\ \\ \frac {(n+1)*n} 2+1(上元素) \end{cases} k=⎩ ⎨ ⎧2(i+1)∗i+j(下和主元素)2(n+1)∗n+1(上元素) - 💡三角矩阵的
-
按列存储
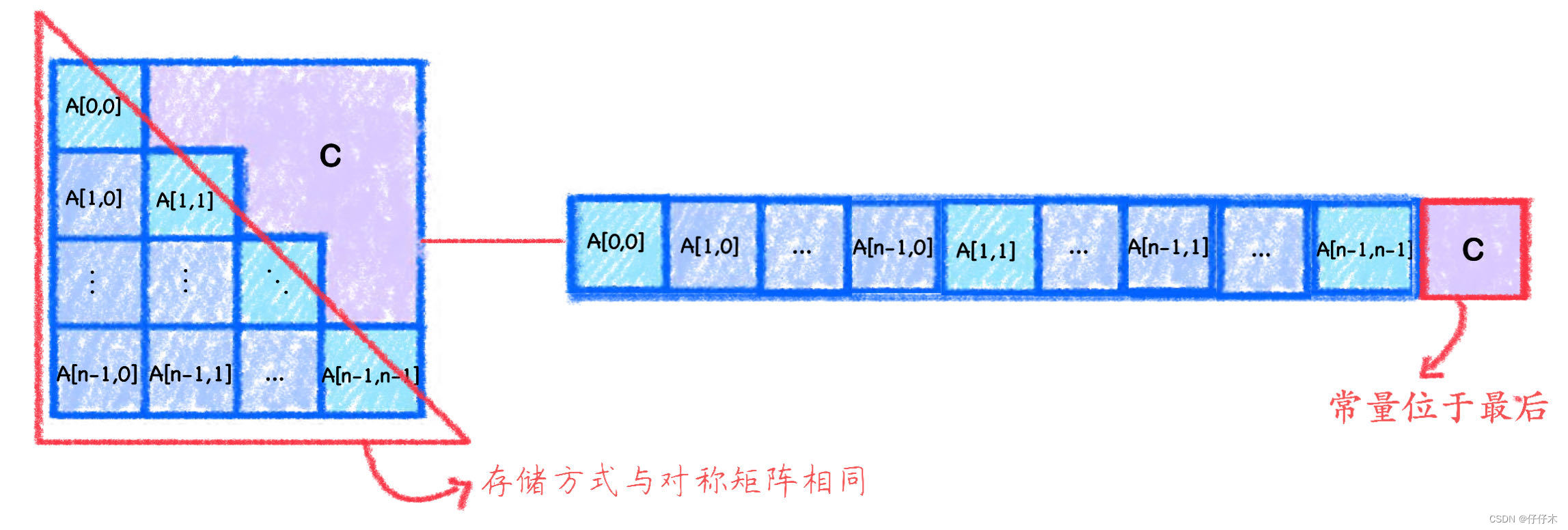
👀看图知:- 💡三角矩阵的
下三角区+主对角线与对阵矩阵存储相同,可直接使用思考三的结论. - 💡三角矩阵的
上三角区的常量存于一维数组的最后,所以位置固定: ( n + 1 ) ∗ n 2 \frac {(n+1)*n} 2 2(n+1)∗n
✅答案:按行排序,二维数组
A[i][j]与B[k]相对应,其中 k = { ( ( 2 n − 1 − j ) ∗ j 2 + i − j ( 下和主元素 ) ( n + 1 ) ∗ n 2 + 1 ( 上元素 ) k= \begin{cases} {\frac {((2n-1-j)*j} 2+i-j} (下和主元素) \\ \\ \frac {(n+1)*n} 2+1(上元素) \end{cases} k=⎩ ⎨ ⎧2((2n−1−j)∗j+i−j(下和主元素)2(n+1)∗n+1(上元素) - 💡三角矩阵的
💤思考7:上三角矩阵如何存储❓
-
按行存储
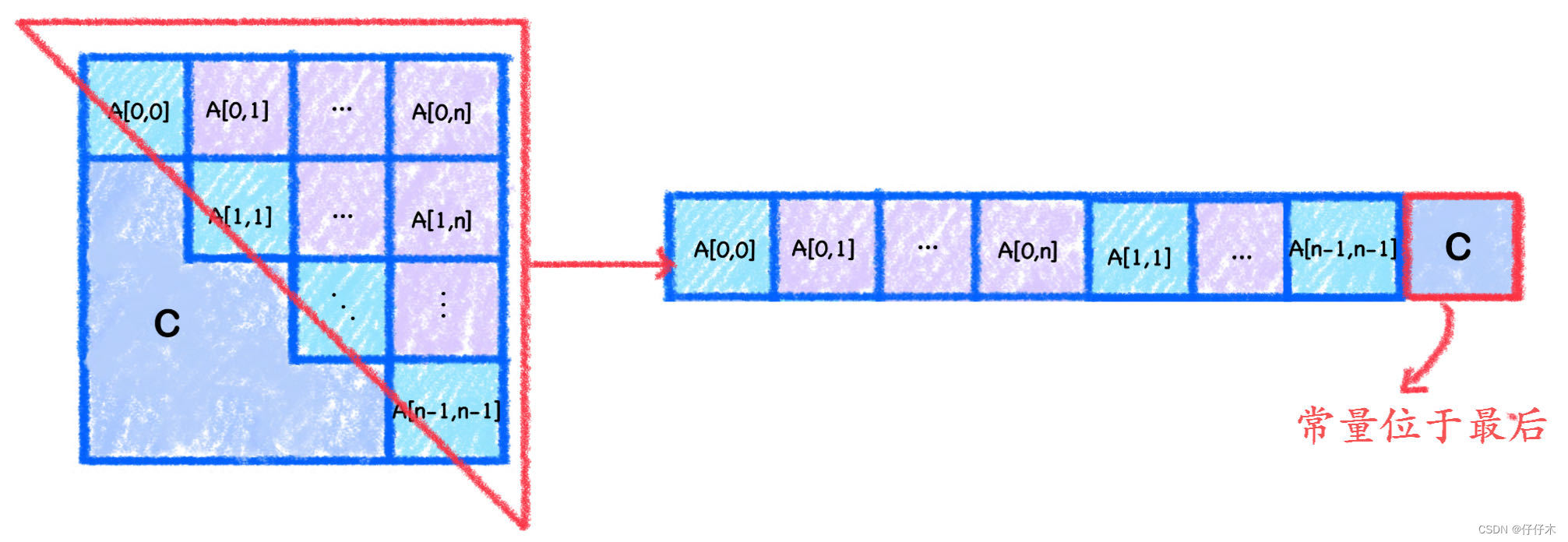
👀图知:- 💡三角矩阵的
上三角区+主对角线与对阵矩阵存储相同,可直接使用思考四的结论. - 💡三角矩阵的
下三角区的常量存于一维数组的最后,所以位置固定: ( n + 1 ) ∗ n 2 \frac {(n+1)*n} 2 2(n+1)∗n
✅答案:按行排序,二维数组
A[i][j]与B[k]相对应,其中 k = { ( ( 2 n − 1 − i ) ∗ i 2 + j − i ( 上和主元素 ) ( n + 1 ) ∗ n 2 + 1 ( 下元素 ) k= \begin{cases} {\frac {((2n-1-i)*i} 2+j-i} (上和主元素) \\ \\ \frac {(n+1)*n} 2+1(下元素) \end{cases} k=⎩ ⎨ ⎧2((2n−1−i)∗i+j−i(上和主元素)2(n+1)∗n+1(下元素)
- 💡三角矩阵的
-
按列存储
👀知:- 💡三角矩阵的
上三角区+主对角线与对阵矩阵存储相同,可直接使用思考四的结论. - 💡三角矩阵的
下三角区的常量存于一维数组的最后,所以位置固定: ( n + 1 ) ∗ n 2 \frac {(n+1)*n} 2 2(n+1)∗n
✅答案:按行排序,二维数组
A[i][j]与B[k]相对应,其中 k = { ( j + 1 ) ∗ j 2 + i ( 上和主元素 ) ( n + 1 ) ∗ n 2 + 1 ( 下元素 ) k= \begin{cases} {\frac {(j+1)*j} 2+i} (上和主元素) \\ \\ \frac {(n+1)*n} 2+1(下元素) \end{cases} k=⎩ ⎨ ⎧2(j+1)∗j+i(上和主元素)2(n+1)∗n+1(下元素) - 💡三角矩阵的
-
3️⃣三对角矩阵
-
三对角矩阵是什么❓
- 💡三对角矩阵又称
带状矩阵 - 💡对于n阶方阵A中的任一元素
a
i
j
a_ij
aij,当
∣
i
−
j
∣
>
1
|i-j|>1
∣i−j∣>1时,有
a
i
j
=
0
(
0
⩽
i
,
j
⩽
n
−
1
)
a_ij=0(0\leqslant i,j\leqslant n-1)
aij=0(0⩽i,j⩽n−1)

- 💡三对角矩阵又称
-
三对角矩阵如何存储❓
💤思考8:有多少个二维元素
A[0...n-1][0...n-1]存于一维元素中❓由上图可知,除了第一行和最后一行为两个元素,其他每行都为三个元素,共有
3*n-2个元素
✅答案:一维数组共需存储 3 ∗ n − 2 3*n-2 3∗n−2个元素💤思考9:按行排序,二维数组
A[0...n-1][0...n-1]与一维数组B[0...3n-3]对应的关系❓
A[i][j]在一维数组B[0...3n-3]的位置:A[i][j]位于第i+1行的第j+1列 第 1 行:共 2 个元素 第 2 行:共 3 个元素 第 3 行:共 3 个元素 ... 第 i 行:共 3 个元素 第i+1行:有j-i+2个元素 求和:2+3+3+...+3+j-i+2=(3i-1)+j-i+2=2i+j+1 B的下标从0开始,所以2i+j+1-1=2i+j,即A[i][j]在一维数组B[2i+j]中✅答案:按行排序,二位数组
A[i][j]与一维数组B[2i+j]对应💤思考10:按列排序,二维数组
A[0...n-1][0...n-1]与一维数组B[0...3n-3]对应的关系❓
A[i][j]在一维数组B[0...3n-3]的位置:A[i][j]位于第i+1行的第j+1列 第 1 列:共 2 个元素 第 2 列:共 3 个元素 第 3 列:共 3 个元素 ... 第 j 列:共 3 个元素 第j+1列:有i-j+2个元素 求和:2+3+3+...+3+i-j+2=(3j-1)+i-j+2=2j+i+1 B的下标从0开始,所以2j+i+1-1=2j+i,即A[i][j]在一维数组B[2j+i]中✅答案:按列排序,二位数组
A[i][j]与一维数组B[2j+i]对应

三、稀疏矩阵
- 什么样的矩阵是稀疏矩阵❓
💡非零元素远远少于矩阵元素个数
例:100*100矩阵中,只有100个非零元素。 - 存储方式有哪些❓
-
三元组
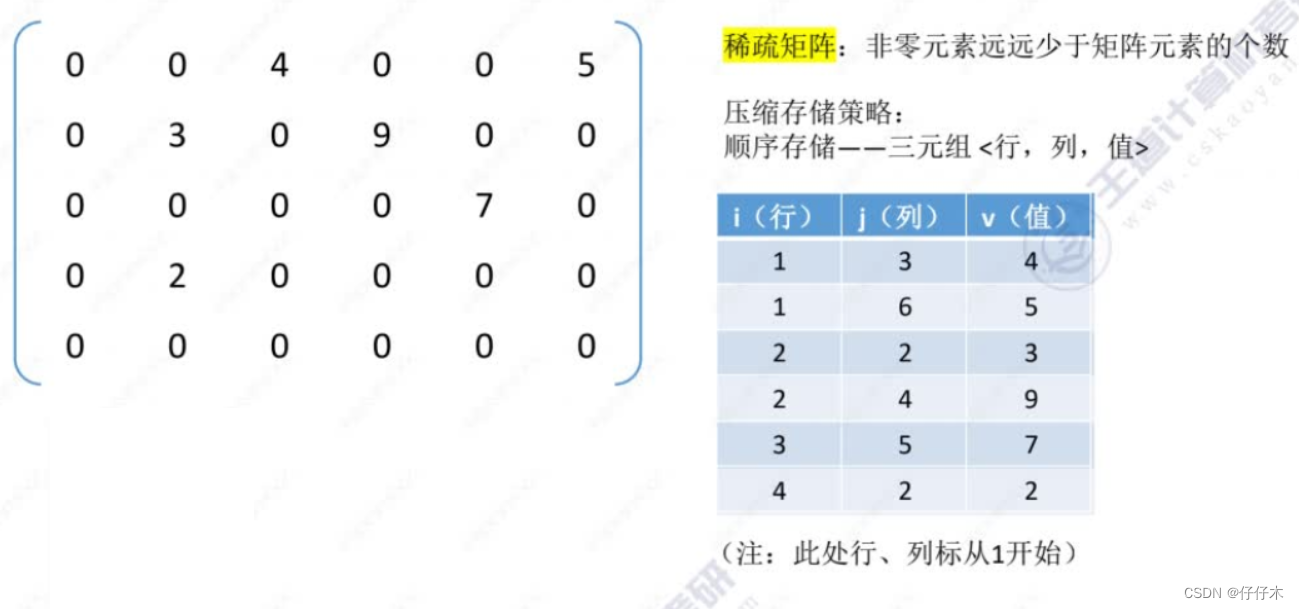
-
十字链表法
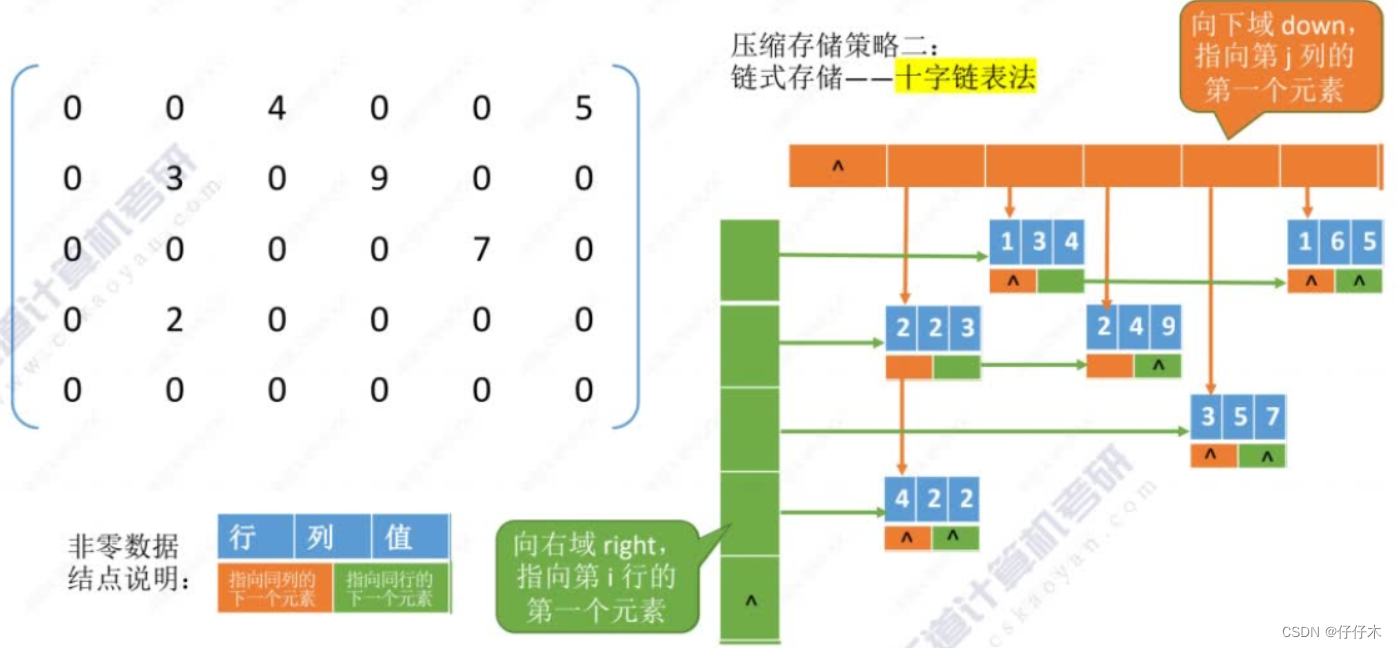
-
参考资料
《王道:23数据结构考研复习指导》






![[NeurIPS 2017] Poincaré Embeddings for Learning Hierarchical Representations](https://img-blog.csdnimg.cn/c983d9214c8a43119bebe6dd8c99b640.png#pic_center)