网络
网络是一张单向图 , 每条边都有一个权值 c ( u , v ) c(u,v) c(u,v) 表示边 ( u , v ) (u,v) (u,v) 的容量. 特别的 , 图上有源点 ( s ) (s) (s) 和汇点 ( t ) (t) (t).
网络流
在一张网络上 , 从源点流出 , 最终流入汇点的流.
f ( u , v ) f(u,v) f(u,v) 表示 ( u , v ) (u,v) (u,v) 的流量.
满足 :
- 容量限制 : f ( u , v ) ≤ c ( u , v ) f(u,v)\le c(u,v) f(u,v)≤c(u,v)
- 流量平衡 : 对于非 s , t s,t s,t 的点 x x x 要求流入 x x x 的流量量等于流出 x x x 的流量 , 即 ∑ f ( u , x ) = ∑ f ( x , u ) \sum f(u,x)=\sum f(x,u) ∑f(u,x)=∑f(x,u).
- 斜对称性 : f ( u , v ) = − f ( v , u ) f(u,v)=-f(v,u) f(u,v)=−f(v,u) ( 相当于反悔机制 )
网络流的应用
网络最大流
在一张网络上 , 给定源点 s s s 汇点 t t t , 要求 f ( u , v ) ≤ c ( u , v ) f(u,v)\le c(u,v) f(u,v)≤c(u,v) , 求一条 s s s 到 t t t 的最大流
题目
若边 ( u , v ) (u,v) (u,v) 满足 f ( u , v ) < c ( u , v ) f(u,v)<c(u,v) f(u,v)<c(u,v) 我们称这条边是有潜力的 , c ( u , v ) − f ( u , v ) c(u,v)-f(u,v) c(u,v)−f(u,v) 称为这条边的潜力值
如果存在一条从 s s s 到 t t t 的路径 , 该路径上的所有边都有潜力 , 我们显然可以将这条路径上的流增加这些边中最小的潜力值 , 该操作称为增广. 可用 dfs 或 bfs 判断网络上是否存在可增广的路径.
在反悔机制的基础上 , 保证了该策略的正确性 , 该算法称为 E K EK EK 算法
那么核心代码即为
while( 可增广 )
增广 ;
时间复杂度 O ( n 2 m ) O(n^2m) O(n2m)
code
无源汇有上下界可行流
题目 / 题目
在一张网络上 , 要求 l ( u , v ) ≤ f ( u , v ) ≤ r ( u , v ) l(u,v)\le f(u,v)\le r(u,v) l(u,v)≤f(u,v)≤r(u,v) , 问是否存在可行流
l ≤ f ( u , v ) ≤ r l \le f(u,v) \le r l≤f(u,v)≤r , 记 f ′ ( u , v ) = f ( u , v ) − l f'(u,v)=f(u,v)-l f′(u,v)=f(u,v)−l
即 0 ≤ f ′ ( u , v ) ≤ r − l 0\le f'(u,v) \le r-l 0≤f′(u,v)≤r−l 即为一般网络流形式
例如 :
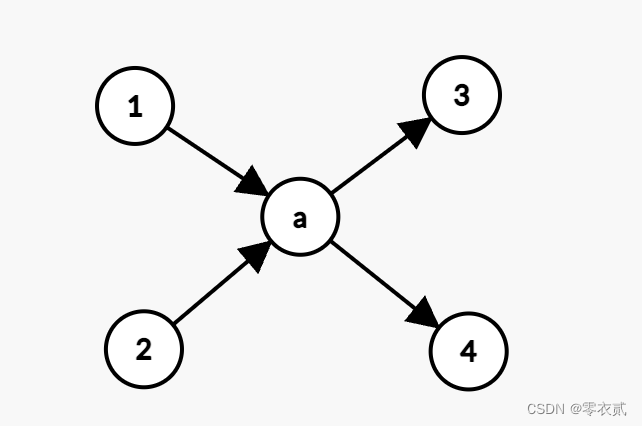
根据流量平衡 , 有 :
f
′
(
1
,
a
)
+
f
′
(
2
,
a
)
+
i
n
a
=
f
′
(
a
,
3
)
+
f
′
(
a
,
4
)
+
o
u
t
a
f'(1,a)+f'(2,a)+in_a=f'(a,3)+f'(a,4)+out_a
f′(1,a)+f′(2,a)+ina=f′(a,3)+f′(a,4)+outa
i n a = l ( 1 , a ) + l ( 2 , a ) , o u t a = l ( 1 , a ) + l ( 2 , a ) in_a=l(1,a)+l(2,a), out_a=l(1,a)+l(2,a) ina=l(1,a)+l(2,a),outa=l(1,a)+l(2,a)
因此我们可以建立一个超级源点与超级汇点
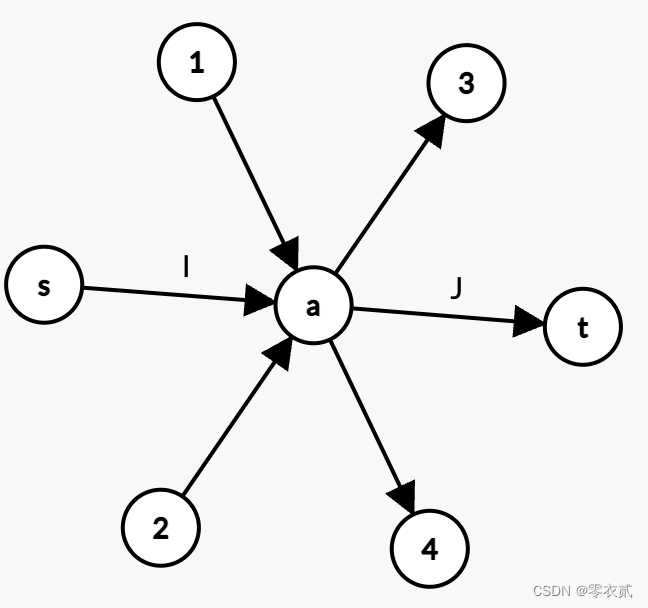
原方程 f ( 1 , a ) + f ( 2 , a ) = f ( a , 3 ) + f ( a , 4 ) f(1,a)+f(2,a)=f(a,3)+f(a,4) f(1,a)+f(2,a)=f(a,3)+f(a,4) 有解
当且仅 f ′ ( 1 , a ) + f ′ ( 2 , a ) + i n a = f ′ ( a , 3 ) + f ′ ( a , 4 ) + o u t a f'(1,a)+f'(2,a)+in_a=f'(a,3)+f'(a,4)+out_a f′(1,a)+f′(2,a)+ina=f′(a,3)+f′(a,4)+outa 有解.
将 ( s , a ) (s,a) (s,a) 的上限为 i n a in_a ina , ( a , t ) (a,t) (a,t) 的上限为 o u t a out_a outa . 根据上文的代码 , 满足平衡条件的情况下保证了流量最大 , 因此如果最大流达到了所有 i n a in_a ina 的上限 (此时同样满足所有 o u t a out_a outa 的上限) , 方程一定有解.
记录
code

![[NeurIPS 2017] Poincaré Embeddings for Learning Hierarchical Representations](https://img-blog.csdnimg.cn/c983d9214c8a43119bebe6dd8c99b640.png#pic_center)
![[Windows] 微信超级管家,自动好友回复、计数、自动同意、群发、好友导出、消息日志、无限多开](https://img-blog.csdnimg.cn/ffc73d3d8a7b49f9971451c83b47957b.png#pic_center)