图解LeetCode——1145. 二叉树着色游戏（难道：中等）

news2024/11/23 0:55:22

一、题目

有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中，给出二叉树的根节点 root，树上总共有 n 个节点，且 n 为奇数，其中每个节点上的值从 1 到 n 各不相同。最开始时：

「一号」玩家从 [1, n] 中取一个值 x（1 <= x <= n）；
「二号」玩家也从 [1, n] 中取一个值 y（1 <= y <= n）且 y != x。

「一号」玩家给值为 x 的节点染上红色，而「二号」玩家给值为 y 的节点染上蓝色。之后两位玩家轮流进行操作，「一号」玩家先手。每一回合，玩家选择一个被他染过色的节点，将所选节点一个 未着色 的邻节点（即左右子节点、或父节点）进行染色（「一号」玩家染红色，「二号」玩家染蓝色）。如果（且仅在此种情况下）当前玩家无法找到这样的节点来染色时，其回合就会被跳过。若两个玩家都没有可以染色的节点时，游戏结束。着色节点最多的那位玩家获得胜利 ✌️。现在，假设你是「二号」玩家，根据所给出的输入，假如存在一个 y 值可以确保你赢得这场游戏，则返回 true ；若无法获胜，就请返回 false 。

二、示例

示例 1 ：

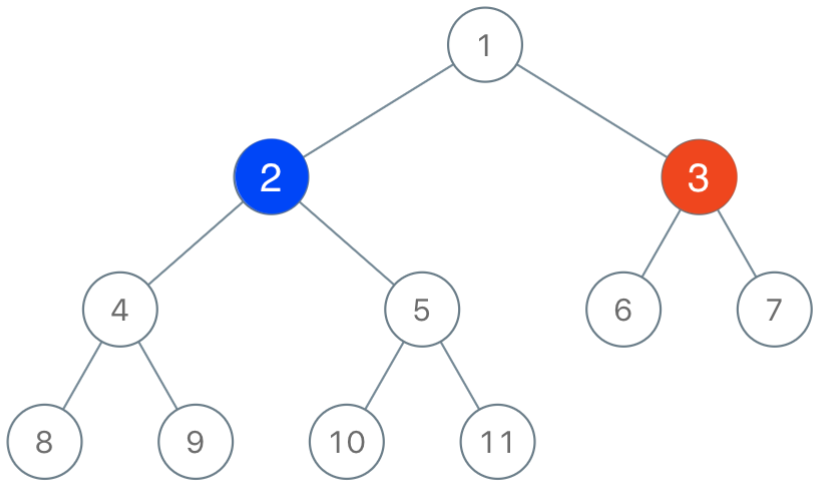
【输入】：root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
【输出】：true
【解释】：第二个玩家可以选择值为 2 的节点。

示例 2 ：

【输入】root = [1,2,3], n = 3, x = 1
【输出】false

提示：

树中节点数目为 n
1 <= x <= n <= 100
n 是奇数
1 <= Node.val <= n
树中所有值 互不相同

三、解题思路

根据题目描述，我们其实可以知道一号玩家是先手的，那么他第一次落子的位置，就决定着我们作为二号选手是否有机会能赢得比赛。我们以下图中的节点为例，假设一号选手选择了节点2这个位置落下了第一个棋子，那么如果二号选手选择了节点3，那么我们就可以将整个树节点划分为如下3个区域，如下图所示：

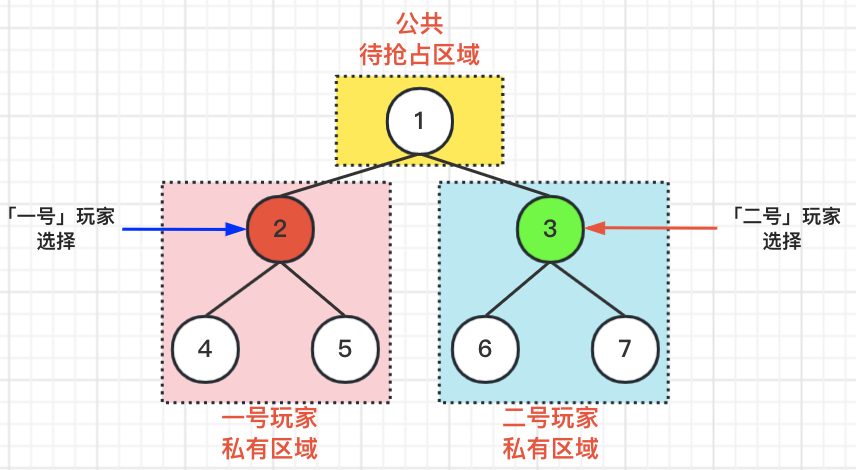
【区域1】公共待抢占区域：Node(1)
【区域2】一号玩家私有区域：Node(2)，Node(4)，Node(5)
【区域3】二号玩家私有区域：Node(3)，Node(6)，Node(7)

那么，我们对上面的逻辑清晰了之后，其实就可以得出一个解题思路，就是我们只需要根据一号选手第1次落子（firstNode）的位置来计算3种情况，即：

【情况1】二号选手落子在firstNode的左子节点上时，二号选手私有区域是否大于总数的一半。
【情况2】二号选手落子在firstNode的右子节点上时，二号选手私有区域是否大于总数的一半。
【情况3】二号选手落子在firstNode的根节点节点上时，二号选手私有区域是否大于总数的一半。

如果满足上面的3个情况任意一种，则二号选手就有获胜的可能了。那么，问题来了，_为啥只关注了私有区域却没有关注公有区域呢？_原因就是，因为一号选手是先手的，他本来就在落子顺序上占据了先机，那么对于占用公有区域的操作来说，一号选手也是具有先手的优势的。所以，对于二号选手的获胜条件只能是，自己的私有区域要足够的大。

解题思路说完了，下面我们就以例子来看一下，具体逻辑如下图所示：

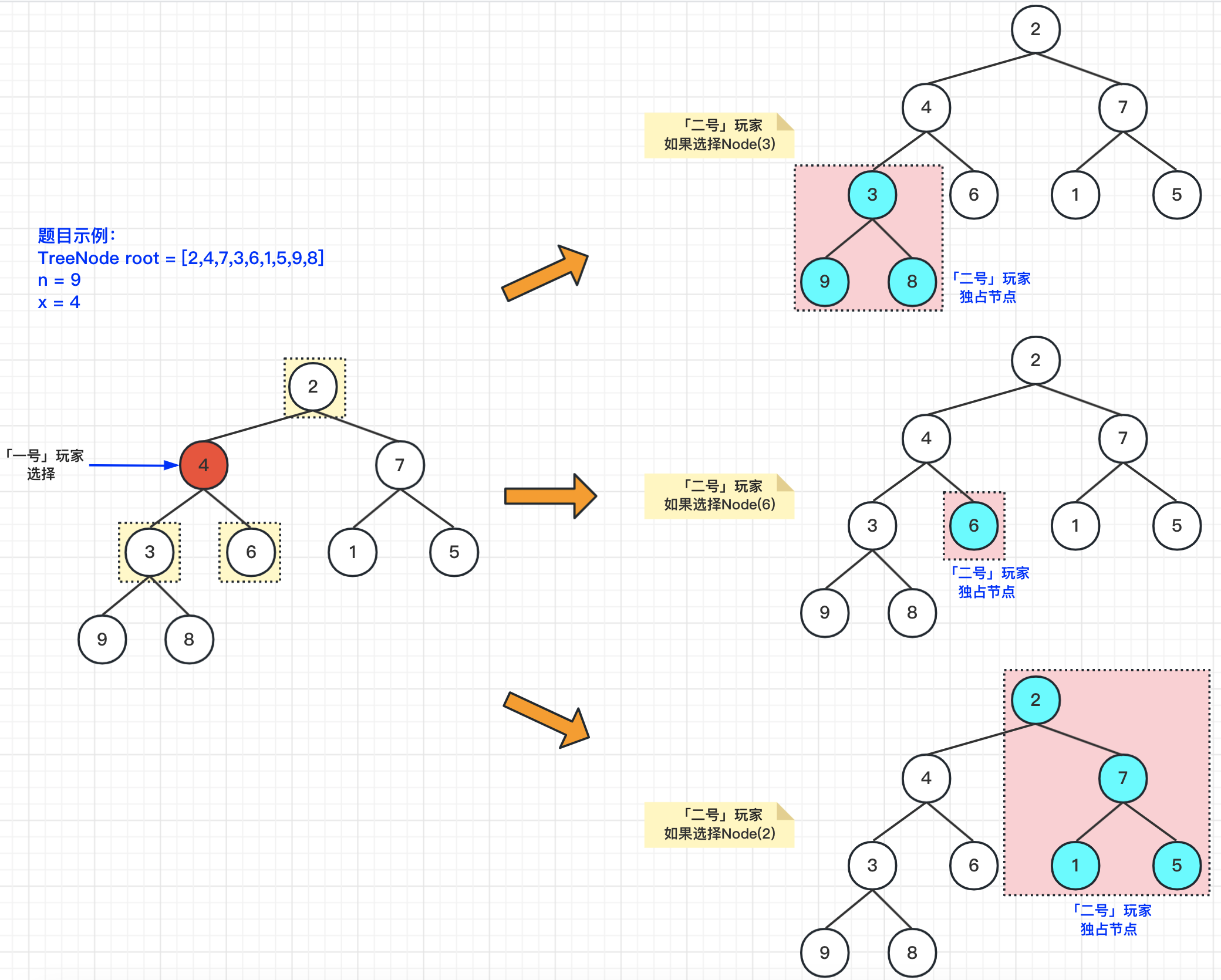
四、代码实现

class Solution {
    int ltnc = 0, rtnc = 0;
    public boolean btreeGameWinningMove(TreeNode root, int n, int x) {
        nodeCount(root, x);
        return 2*ltnc > n || 2*rtnc > n || 2*(ltnc + rtnc + 1) < n;
    }
    public int nodeCount(TreeNode t, int v) {
        if (t == null) return 0;
        int lc = nodeCount(t.left, v);
        int rc = nodeCount(t.right, v);
        if (t.val == v) { // 找到x选择的node，开始记录这个node的左子树和右子树的节点个数
            ltnc = lc;
            rtnc = rc;
        }
        return lc + rc + 1;
    }
}