题意：这题目一开始看了半天啊，而且坑点很多（qwq），大概意思就是给你两个字符串a,b（可能存在前导0），然后给你任意个长度为10的从0到9的排列（比如1234567890 ，0923475618...）

让你把这a,b这两个字符串的每一位进行转换，就是根据排列的位置进行转换，假如a的第一个字符是'9'，排列是”0923475618“，那么转化之后的字符是这个排列的字符串的下标对应的字符'1'。

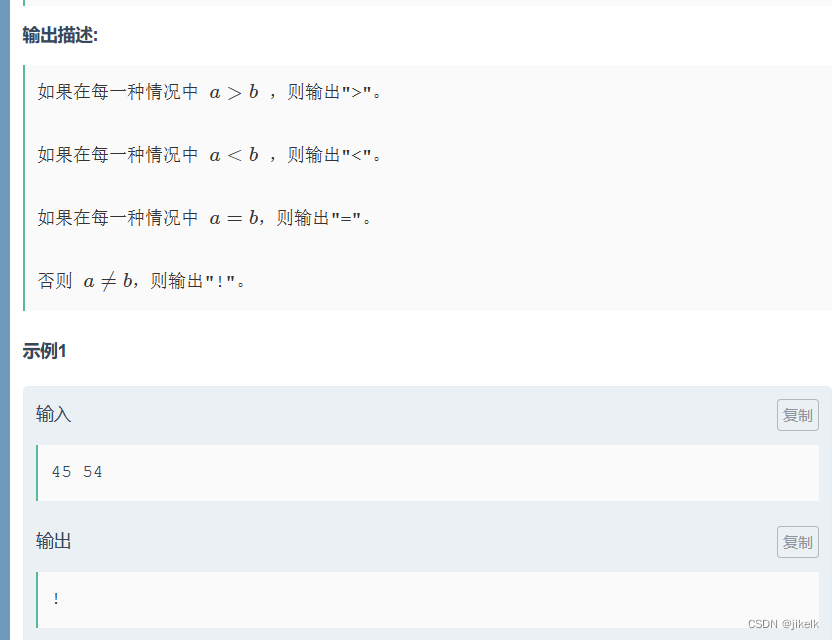
之后给我们转换之后的字符串A，B，然后问对于所有的情况排列，是否存在ab之间有一定的大小（或者等于）的关系，如果有就输出对应关系，如果没有，就输出"!"。

思路：因为对于所有的排列情况，根据排列的不同，ab的大小关系也很有可能发生变化（比如A=54,B=45在排列p=1234567890和p=0987654321就是刚好的相反的关系），所以我们不能根据最后得到的AB来简单的进行大小的判断。

于是我们可以逐步分析，从两个字符串的长度相等与否来进行分析：

1.A,B字符串长度相同的情况（即a,b字符串长度相等）：

如果这两个字符串的长度是相同的话，那么可以简单的得到一个结论：

如果A完全等于B，即a==b（因为如果a==b那么这两个字符串在排列种对应得到的字符串也是完全一致的，反之也成立），否则a!b.

为什么没有大于或者小于的情况了？

因为如果对于两个长度相同的字符串来说，如果他们两个不完全相同，那么就是他们的第一个字符不相同，那么对于长度相同但是第一个字符不同的两个字符串来说，只要这两个字符对应在排列里的下标交换一下顺序，他们两个的大小关系就会发生改变，更不用谈所有情况的排列q了。

好，现在来到坑点众多的重头戏，

2.A,B字符串长度不相同的情况（即a,b字符串长度不等）：

乍一看长度不相同，位数都不一样，按道理应该是长度大的那一位始终大于，但是我们要考虑到题目中说过的一句话，这句话存在的意思是什么呢，就是说AB转化之前的ab有前导0的情况（好像是废话？！），那么如果存在前导0，

那么转换前，和转换后的字符串长度其实就不相同了（前导0因为不用来比大小所以不算）

比如：a是000234 排列p=1043526789 ，那么转换后的A为111435，a中本来不作为比较大小的0经过转换多增加了三位。

我们可以根据例子发现，字符串有前导零的情况，多增加的字符串为A中连续且相等的前i个字符（）n为字符串长度。

 

那么我们可以将长度大的那个字符串，取可能为前导零的那一部分（如果取长度小的字符串那就会变的更小），假设为前导零（同时定义个变量表示前导零的那个字符si），然后比较去除前导零后剩下的两个字符串，如果去除后的字符串还是大于另一个字符串的话，就可以说明在任意的排列的情况下有确定的大小关系。

那么怎么根据剩下的字符串来判断大小关系呢？

假设去除前导零后的字符串为_a,_b（两个都要去除，因为都是根据某一个排列进行转换的），如果两个字符串的位数不一样，那么可以很明显的得到_a,_b这两个字符串的大小了，否则就是位数一样的情况，这个时候别急着说没有大小关系了，我们可以从第一位到最后一位逐位判断，如果每一位都相同，那么结果肯定是'!'，如果这一位两个字符不相同，那么也有三种情况：

1.和都不是前导零的那个字符si，那么这两者的大小情况不能判断，那么就是！

2.如果是那个前导0的字符，那么因为转换前是0，所以无论_b字符串在当前这一位是什么一定会比0大，所以一定是_b>_a。

3.如果是位前导零的字符，根据（2）同理可得一定为_a>_b.

那么字符串的大小就可以直接比较出来了，然后就可以得到最终的结果啦！

ps：这次又写了很长的一篇解析，主要是自己当时做的时候情况分析的太不好了，所以这次想全面的分析一下，如果觉得写的不好其实也无所谓啦（反正是写给自己的

代码：（自己写的代码太屎山了看了蒋佬的还是自愧不如，于是用的是蒋佬的思想然后自己敲了一遍的）

/**
*　　┏┓　　　┏┓+ +
*　┏┛┻━━━┛┻┓ + +
*　┃　　　　　　　┃
*　┃　　　━　　　┃ ++ + + +
*  ████━████+
*  ◥██◤　◥██◤ +
*　┃　　　┻　　　┃
*　┃　　　　　　　┃ + +
*　┗━┓　　　┏━┛
*　　　┃　　　┃ + + + +Code is far away from 　
*　　　┃　　　┃ + bug with the animal protecting
*　　　┃　 　 ┗━━━┓ 神兽保佑,代码无bug　
*　　　┃ 　	　　　 ┣┓
*　　  ┃ 　　　　　 　┏┛
*　    ┗┓┓┏━┳┓┏┛ + + + +
*　　　　┃┫┫　┃┫┫
*　　　　┗┻┛　┗┻┛+ + + +
*/

#include<cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include<vector>
#include<queue>
#include<map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long 
using namespace std;

const int N=1000000+100;
int n ,m,h;
int s[N];



int main()
{
	int t;
	string a,b;
	cin>>a>>b;
	if(a.size()==b.size())
	{
		if(a==b)cout<<"=\n";
		else cout<<"!\n";
		return 0;
	}

	char ans='>',zero;

	if(a.size()<b.size())
	{
		ans='<';
		swap(a,b);//直接把长度大的字符串定为a
	}

	zero=a[0];

	int n=a.size(),m=b.size();
	for(int i =0;i<n-m;i++)
	{
		if(a[i]!=zero)//多的部分不是全部为前导零
		{
			cout<<ans<<endl;
			return 0;
		}
	}

	 a.erase(a.begin(), a.begin() + n - m);//去除a字符串长度多余的那一部分
    
	if(a==b){
	cout<<"!\n";
	return 0;
	}
	
	 for(int i=0;i<b.size();i++)
	 {
		if(a[i]!=b[i])
		{
			if(b[i]!=zero)//只有b[i]为zero的时候才能保证a>b
			{
				cout<<"!\n";
				return 0;
			}
			break;//b[i]为0
		}
	 }

	cout<<ans<<endl;

	return 0;
}