2024年5月6日15:15:26

专业名词

• DC问题：Difference of Convex 。Difference理解为差，convex是凸，DC问题就是两个凸函数的差的问题。
• SCA：连续凸逼近（Successive Convex Approximation）
• MM算法：Minorize-Maximization、Majorize-Minimization
• CCP：convex-concave procedure凹凸过程
• BCD：Block Coordinate Descent，指的是块坐标下降法
• AO：Alternating Optimization交替优化算法
• gradient projection method 梯度投影法（解决连续松弛）
• 非线性规划：目标函数、约束条件至少一个是决策变量的非线性函数。非线性规划问题包括无约束问题与有约束问题。非线性规划问题引入了不等式约束，标志现代规划理论的开始。
• 无约束最优化：变量轮换法；最速下降法；牛顿法；共轭梯度法；变尺度法
• Quadratic programming：二次规划。
• inf，sup为下确界与上确界，在约束条件下取不到极值max与min

MM算法

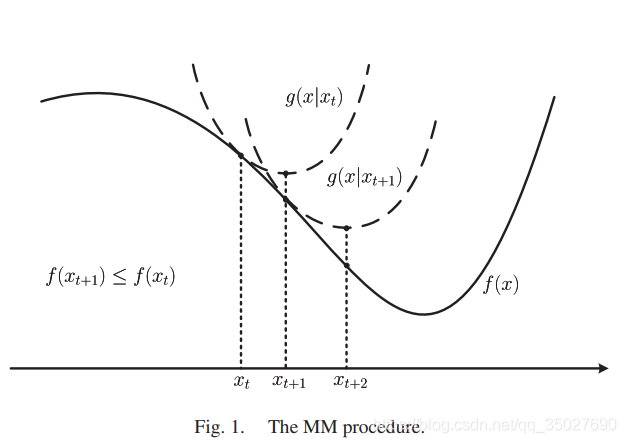
下图为Majorize-Minimization，即求上界的最小值：（构造的g(x)函数为f(x)的上界函数，求g(x)函数的最小值）

CCP算法：

CSDN链接（讲MM和CCP）
知乎链接（讲MM）

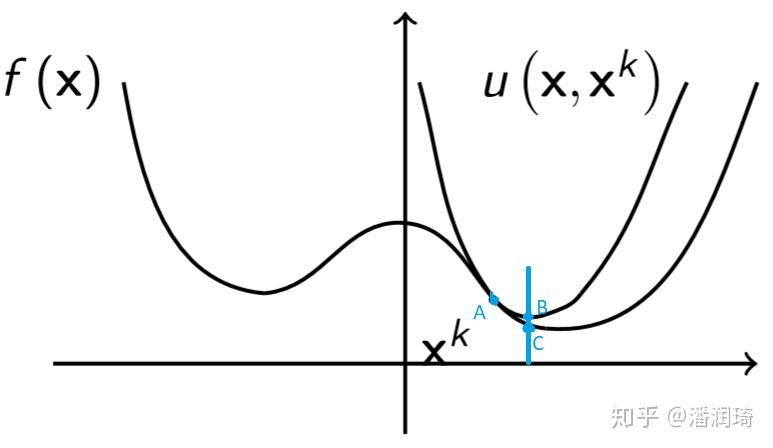
• 每一次要求新构造的可被优化的问题在初始点的值等于原问题在初始点的值，这里一阶泰勒展开是满足的，当$x=x_0$​
  时二者相等。
• 原问题可以被分解为多个凸的子问题，通过求解这些凸的子问题的最小值，来逼近或得到原问题的驻点。
  示例：
  凹凸程序 (Convex-Concave Procedure, CCP) 是用于求解 DC 问题的一种启发式算法。DC 问题（Difference of Convex functions problems）指的是目标函数可被分解为两个凸函数的差值的优化问题。它的形式如下：

$$\underset{x}{\min }f(x)-g(x)$$
其中 (f(x)) 和 (g(x)) 都是凸函数。

算法思路：
CCP 通过在每次迭代中线性近似凹的部分，并将问题转化为凸问题进行优化。基本步骤如下：

1. 给定初始解 (x^0)。
2. 在第 (k) 次迭代中，线性化凹的部分 (g(x))：
   $$g(x)\approx g(x^k)+\nabla g(x^k{)}^T(x-x^k)$$
3. 解以下凸优化问题：
   $$x^{k+1}=\arg \underset{x}{\min }f(x)-\left(g(x^k)+\nabla g(x^k{)}^T(x-x^k)\right)$$
4. 检查收敛条件，如果满足则停止，否则返回步骤 2。

示例代码1（调用函数）：

以下 Python 代码展示了如何使用 CCP 求解一个 DC 问题的示例：

import numpy as np
from scipy.optimize import minimize

# 定义目标函数
def f(x):
    return np.sum(x**2)

def g(x):
    return np.sum(np.abs(x))

# 定义凹凸部分的差值目标函数
def objective(x, g_grad, x_k):
    return f(x) - (g(x_k) + g_grad.T @ (x - x_k))

# 定义梯度计算
def grad_g(x):
    return np.sign(x)

# 函数来求解 DC 问题
def solve_dc(x0, max_iter=100, tol=1e-6):
    x = x0
    for k in range(max_iter):
        g_grad = grad_g(x)
        x_prev = x
        result = minimize(objective, x, args=(g_grad, x_prev), method='L-BFGS-B')
        x = result.x
        if np.linalg.norm(x - x_prev) < tol:
            print(f'Converged after {k + 1} iterations.')
            break
    return x

# 初始化和求解
x0 = np.array([5.0, -3.0, 2.0, -1.0])
x_opt = solve_dc(x0)
print("Optimal solution:", x_opt)

代码说明

1. 目标函数：

   • (f(x))：凸部分的目标函数。
   • (g(x))：凹部分的目标函数。

2. 线性化的凹部分目标函数：

   • 使用 objective 函数来计算线性化后的目标函数。

3. 梯度计算：

   • 使用 grad_g 函数计算凹目标函数的梯度。

4. CCP 算法：

   • solve_dc 函数实现了 CCP 算法，迭代优化目标函数。

示例代码2（手写函数）：

# time: 2024/5/9 10:51
# author: YanJP
import numpy as np

# 定义目标函数
def objective(x):
    return x[0]**2 + x[1]**2

# 目标函数梯度
def grad_objective(x):
    return np.array([2 * x[0], 2 * x[1]])

# 线性化凹部分 d(x, y) 的梯度
def grad_d(x):
    if x[0]**2 > x[1]**2:
        return np.array([x[0], -x[1]])
    else:
        return np.array([-x[0], x[1]])

# 计算线性化后的凸约束部分梯度
def constraint_linearized(x, grad_d, prev_x):
    return 1 - 0.5 * (x[0]**2 + x[1]**2 - grad_d.T @ (x - prev_x))

# 凹凸过程 (CCP) 求解函数
def solve_ccp(x0, max_iter=100, tol=1e-6, step_size=0.1):
    x = x0
    for k in range(max_iter):
        d_grad = grad_d(x)
        grad = grad_objective(x)

        # 线性化凹部分约束
        g_lin = constraint_linearized(x, d_grad, x)

        # 判断线性化后的约束是否满足
        if g_lin > 0:
            x_new = x - step_size * (grad + d_grad)
        else:
            x_new = x - step_size * grad

        if np.linalg.norm(x_new - x) < tol:
            print(f'Converged after {k + 1} iterations.')
            break

        x = x_new

    return x

# 初始值
x0 = np.array([2.0, 2.0])
x_opt = solve_ccp(x0)
print("Optimal solution:", x_opt)
print("Objective value:", objective(x_opt))

SCA算法：

添加链接描述。注意和MM进行对比：SCA 要求近似函数是凸函数 而MM要求近似函数在近似点是原函数的upper bound。

连续松弛

51blog

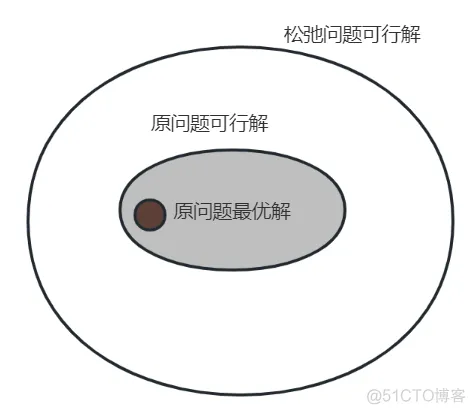
• 对于松弛优化问题R和原优化问题P，如果满足
  • (i)每一个P的可行解在R中也都可行
  • （ii）P中每个可行解在R中的目标值与其在P中的目标相比都相等或更好，
    那么优化问题R是优化问题P的松弛。
    
    上图的意思就是：松弛模型提供了原问题最优解的确界(最大值问题是上界，最小问题是下界)。

梯度投影算法

csdn（讲的可以）
比较专业

分支定界搜索法

凸问题辨别

原文链接：

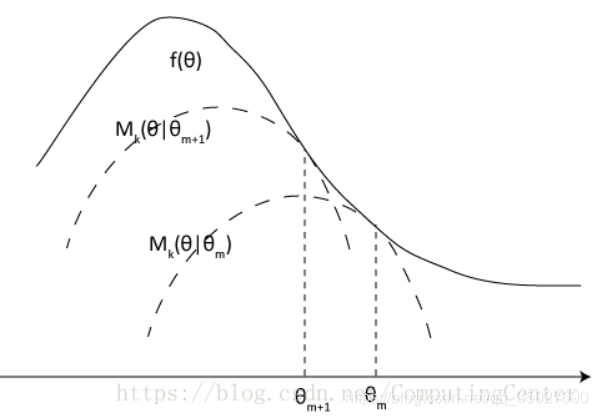
• 无论是该和速率是作为目标函数，还是作为约束，都不是凸函数的形式，原因是涉及到 log()+log() 的形式，是非凸的。
• 常见解决方法，是采用迭代的方法，即采用 凸差 / 连续凸近似 / MM算法 （这三种算法的思想都是类似的），在每次迭代的过程中，用目标函数的下界（此时是凸的,如下图） 去替换原来的目标函数，那么，对每次迭代时，新的目标函数都是凸的，且每次的解出的结果都是原函数的下界。且迭代过程期间所得到解是递增的
  

OA算法

知乎（有代码）

λ-representation

在凸优化中，λ-representation（也称为Lagrange 表示）是一种用于描述凸集的方法。它通过使用一组凸组合的方式来表示凸集，其中每个凸组合的权重由一组非负的 Lagrange 乘子${\lambda }_i$ 决定。λ-representation 是在凸优化理论中广泛应用的概念，特别是在描述凸包、凸锥和凸函数等方面。

λ-representation 的一般形式可以表示为：

C = { x ∈ R n   ∣   x = ∑ i = 1 m λ i x i ,   x i ∈ C ,   λ i ≥ 0 ,   ∑ i = 1 m λ i = 1 } C = \{ x \in \mathbb{R}^n \ |\ x = \sum_{i=1}^{m} \lambda_i x_i, \ x_i \in C, \ \lambda_i \geq 0, \ \sum_{i=1}^{m} \lambda_i = 1 \} C={x∈Rn ∣ x=i=1∑m​λi​xi​, xi​∈C, λi​≥0, i=1∑m​λi​=1}

其中，$C$ 是凸集，$x_i$是$C$ 中的点，${\lambda }_i$ 是非负的 Lagrange 乘子，且满足${\sum }_{i=1}^m{\lambda }_i=1$。这表示 $C$中的任意点都可以通过一组凸组合来表示。

λ-representation 的优点之一是它提供了一种紧凑且直观的表示凸集的方式，特别是在某些情况下，当凸集的结构比较复杂或难以直接描述时，λ-representation 可以提供一种简单的方法来描述凸集。

ADMM算法

知乎
基本概念：

• ADMM 将优化问题分解成两个或多个更容易求解的子问题，通过引入拉格朗日乘子进行迭代。
• 其基本思想来源于拉格朗日乘子法和增广拉格朗日函数。

特征：

1. 适用范围：用于带有线性约束和非光滑正则化的优化问题，例如 LASSO 和约束优化问题。
2. 问题分解：将原始问题分解成多个子问题，逐个优化各个变量块。
3. 拉格朗日乘子：通过引入拉格朗日乘子，实现子问题之间的信息共享。
4. 非光滑正则化：能够处理带非光滑正则项的问题（如 L1 正则项）。

公式：
给定优化问题：
$$\underset{x,z}{\min }f(x)+g(z),\text{s.t.}Ax+Bz=c$$
ADMM 将其转化为以下形式：

1. 更新 (x)：
   $$x^{k+1}=\arg \underset{x}{\min }\left(f(x)+\frac{\rho }{2}\Vert Ax+B{z}^k-c+u^k{\Vert }_2^2\right)$$
2. 更新 (z)：
   $$z^{k+1}=\arg \underset{z}{\min }\left(g(z)+\frac{\rho }{2}\Vert A{x}^{k+1}+Bz-c+u^k{\Vert }_2^2\right)$$
3. 更新乘子 (u)：
   $$u^{k+1}=u^k+A{x}^{k+1}+B{z}^{k+1}-c$$
   在交替方向乘子法 (ADMM) 中，u 是拉格朗日乘子，z 是引入的辅助变量，用于分解问题。通过 z 和 u，可以将问题分解为更容易处理的子问题。

在 LASSO 问题中，目标函数：
$$\underset{\beta }{\min }\frac{1}{2}|X\beta -y{|}_2^2+\lambda |\beta {|}_1$$
目标函数被拆分成以下两个部分：

1. 子问题 1（更新 (\beta)）：
   $${\beta }^{k+1}=\arg \underset{\beta }{\min }\frac{1}{2}\Vert X\beta -y{\Vert }_2^2+\frac{\rho }{2}\Vert \beta -z^k+u^k{\Vert }_2^2$$

2. 子问题 2（更新 (z)）：
   $$z^{k+1}=\arg \underset{z}{\min }\lambda \Vert z{\Vert }_1+\frac{\rho }{2}\Vert {\beta }^{k+1}-z+u^k{\Vert }_2^2$$

3. 更新 (u)（拉格朗日乘子）：
   $$u^{k+1}=u^k+({\beta }^{k+1}-z^{k+1})$$

完整的 Python 实现：

import numpy as np

# 生成随机数据
np.random.seed(0)
m, n = 100, 20
X = np.random.randn(m, n)
beta_true = np.random.randn(n)
y = X @ beta_true + 0.1 * np.random.randn(m)

# ADMM 参数
rho = 1.0
alpha = 1.0
lambda_lasso = 0.1
max_iter = 1000
abs_tol = 1e-4
rel_tol = 1e-3

# 初始值
beta = np.zeros(n)
z = np.zeros(n)
u = np.zeros(n)

# 定义软阈值算子
def soft_threshold(x, kappa):
    return np.sign(x) * np.maximum(np.abs(x) - kappa, 0)

# 预计算常数
X_T_X = X.T @ X
L = np.linalg.cholesky(X_T_X + rho * np.eye(n))

def solve_admm(X, y, lambda_lasso, rho, alpha, max_iter, abs_tol, rel_tol):
    n = X.shape[1]
    beta = np.zeros(n)
    z = np.zeros(n)
    u = np.zeros(n)
    
    X_T_X = X.T @ X
    L = np.linalg.cholesky(X_T_X + rho * np.eye(n))
    L_T = L.T
    
    for k in range(max_iter):
        # 更新 beta
        q = X.T @ y + rho * (z - u)
        beta = np.linalg.solve(L, np.linalg.solve(L_T, q))

        # 更新 z
        z_old = z.copy()
        beta_hat = alpha * beta + (1 - alpha) * z_old
        z = soft_threshold(beta_hat + u, lambda_lasso / rho)

        # 更新 u
        u += beta_hat - z

        # 计算误差
        r_norm = np.linalg.norm(beta - z)
        s_norm = np.linalg.norm(-rho * (z - z_old))
        eps_pri = np.sqrt(n) * abs_tol + rel_tol * max(np.linalg.norm(beta), np.linalg.norm(z))
        eps_dual = np.sqrt(n) * abs_tol + rel_tol * np.linalg.norm(rho * u)

        if r_norm < eps_pri and s_norm < eps_dual:
            break

        if k % 100 == 0:
            print(f'Iteration {k}, r_norm = {r_norm:.4f}, s_norm = {s_norm:.4f}')

    return beta

# 求解 LASSO 问题
beta_est = solve_admm(X, y, lambda_lasso, rho, alpha, max_iter, abs_tol, rel_tol)
print("Estimated coefficients:", beta_est)

代码说明

1. solve_admm 函数：

   • 用 numpy.linalg.solve 求解 \beta 子问题。
   • 使用 soft_threshold 函数实现软阈值算子，解决 (z) 子问题。
   • 更新拉格朗日乘子 (u)。

2. soft_threshold 函数：

   • 用于执行 L1 正则化的阈值运算。

3. Cholesky 分解：

   • 用于加速 (\beta) 子问题的求解过程。

BCD算法

交替方向乘子法 (ADMM) 和块坐标下降法 (BCD) 都是用于求解优化问题的分解方法，但它们在处理优化问题的方式和应用场景上存在显著区别。以下是两者的主要区别和应用场景：

BCD（Block Coordinate Descent）

基本概念：

• BCD 通过逐次优化目标函数的一个子集变量来迭代接近最优解。
• 每次只更新一个或一组变量（块），保持其他变量固定。

特征：

1. 适用范围：用于目标函数分解成不同块（子集）独立优化的情况。
2. 块分解：问题被分解为多个块，在每个块内优化子问题。
3. 逐块优化：保持其他变量固定，优化目标函数的一部分（通常使用梯度或闭式解）。

公式：
对于优化问题：
$$\underset{x}{\min }f(x_1,x_2,\dots ,x_k)$$
其中 $x=(x_1,x_2,\dots ,x_k)$被划分成 (k) 个块，BCD 的过程如下：

1. 更新第一个块 (x_1)：
   $$x_1^{k+1}=\arg \underset{x_1}{\min }f(x_1,x_2^k,x_3^k,\dots ,x_k^k)$$
2. 更新第二个块 (x_2)：
   $$x_2^{k+1}=\arg \underset{x_2}{\min }f(x_1^{k+1},x_2,x_3^k,\dots ,x_k^k)$$
3. 重复对每个块进行更新，直到所有块都更新完成。

代码示例

该Python函数block_coordinate_descent实现了一个基于块坐标下降法（Block Coordinate Descent, BCD）的算法，用于求解具有正定矩阵Hessian的无约束优化问题。具体来说，它最小化的目标函数形式为：
$$f(\mathbf{x})=\frac{1}{2}{\mathbf{x}}^T\mathbf{Qx}+{\mathbf{c}}^T\mathbf{x}$$
其中，$(\mathbf{Q})$是一个正定矩阵，$\mathbf{c}$是一个常数向量，而$\mathbf{x}$是我们要找的向量解。以下是函数详细步骤的分解：
输入参数说明：

1. Q (np.ndarray): 正定矩阵，定义了目标函数的二次项。
2. c (np.ndarray): 向量，定义了一次项系数。
3. max_iter (int, 默认为1000): 最大迭代次数。
4. tol (float, 默认为1e-5): 收敛容差，当连续两次迭代解之间的L2范数差小于这个值时，认为算法已收敛。
   函数执行流程：
5. 初始化: 初始化解向量 (\mathbf{x}) 为全零向量，长度与 (\mathbf{c}) 相同。
6. 迭代过程:
   对于每个迭
7. 代次数 iteration（从0到max_iter-1）： 保存旧解: 复制当前解 $\mathbf{x}$ 到
   ${\mathbf{x}}_{old}$，用于后续的收敛性检查。 循环更新坐标: 遍历每个坐标 (i)（从0到n-1，其中 n = len(c)）： 计算梯度分量: 计算目标函数在第 (i) 个坐标上的导数分量，这涉及到矩阵 $\mathbf{Q}$ 的对角元素$Q_{ii}$，以及与其余坐标相关的线性组合。
8. 更新坐标值: 根据计算出的梯度分量，使用封闭形式的解来直接更新$\mathbf{x}[i]$。
9. 检查收敛: 计算新解 $\mathbf{x}$与旧解${\mathbf{x}}_{old}$之间的L2范数差，若差值小于预设的 tol，则认为算法已收敛，并打印收敛信息，包括迭代次数，然后跳出循环。 返回结果: 如果达到最大迭代次数仍未收敛，也会返回最后的解$\mathbf{x}$。

特点与适用场景：
优点: BCD方法特别适合处理大规模优化问题，因为它每次只更新一个坐标，减少了每轮迭代的计算复杂度，尤其是在 $\mathbf{Q}$ 是稀疏或具有特殊结构时。
适用性: 适用于具有大量变量但可以有效独立处理各个变量的优化问题，如稀疏信号恢复、机器学习中的正则化问题等。
综上所述，此函数提供了一个高效求解特定形式优化问题的实现，利用了块坐标下降法的迭代更新策略，旨在找到使目标函数取最小值的向量 $\mathbf{x}$。
更新公式: 根据牛顿法或梯度下降法，我们可以写出 (x_i) 的更新规则，即减去梯度方向上的一步大小。这里的目标函数关于 (x_i) 的梯度是$(-Q_{ii}{x}_i-c_i-{\sum }_{j\ne i}{Q}_{ij}{x}_j)$。将 $(x_i)$ 从梯度中分离出来，得到上述更新规则，即 (x_i) 的新值等于旧值乘以 (-1)，再除以 $(Q_{ii})$，并加上$Q_i^{rest}\ast x_i^{rest}+c_i$ 的相反数

更新第 i 个坐标
x[i] = - (Q_i_rest @ x_i_rest + c_i) / Q_ii

与ADMM的区别

1. 问题性质：

   • ADMM：用于含线性约束和非光滑目标的问题（L1 正则化、线性约束）。
   • BCD：通常用于目标函数可分解为多个块的优化问题。

2. 解的精度：

   • ADMM：引入乘子进行拉格朗日松弛，更适用于收敛到全局最优解。
   • BCD：块坐标更新容易陷入局部最优解。

3. 迭代方式：

   • ADMM：同时引入乘子变量，通过增广拉格朗日函数更新。
   • BCD：逐个块逐次优化变量子集。

4. 应用场景：

   • ADMM：适用于 LASSO、约束优化、矩阵分解等问题。
   • BCD：用于线性回归、聚类、SVM 优化等问题。

总结

ADMM 和 BCD 在处理复杂的优化问题时具有不同的优缺点和适用场景。选择合适的算法可以更好地解决优化问题。