平衡三进制存算一体架构

news2024/9/19 13:40:49

PS:天天水一贴，快乐又舒心。。。

 1、存算一体概念

        最近想搞平衡三进制的虚拟机，但是写来写去都感觉不对味，能用是能用，但写起来感觉就是很奇怪，用了二种编码，想来想去是不够原生三进制的编写，有点生搬硬套的感觉，所以又去翻翻了图灵他老人家的定义，突然就有了灵感。

        二进制用的是纸带，而三进制多了一个维度，所以应该将高度加上，这样纸带就变成了表格了，这一转变就合理多了，纸带被划分成一系列的方格，每个方格包含一个符号，然后就是状态寄存器及状态转换器，分别用于存储一个表格及转换一个表格，也就是说，只用根据地址取数据和存放数据，它就可以完成相关的运算，也验证了那一句话：算即是存，存即是算。

1.1九九乘法表的应用

        不得不说老祖宗流传下来的东西，确实是博大精深，这下面其实就是一个矩阵了，可将下面的图，转换成矩阵用于计算乘法，电路中没有专用的运算单元，只要能根据地址取数据及存放数据，一样可以完成运算，完美权释了存算一体的概念：算即是存，存即是算。

九九乘法表

        其实很好理解，比如：7*9=63，7和9你可以理解它不是数据值，而一个地址值，地址7及地址9，对应的就是63，这样就是输入数据(相当于地址值)，查询得到新的输出值存起来，这样就完成了一次运算， 将运算得到的规律，制成一个矩阵，这根Chatgpt的训练过程有点像，只不过它不知道九九乘法表，要自己训练出来，而这里是知道了结果，直接将结果应用过去，而不断的矩阵变换，就是运算的过程，真的没想到图灵机的定义，原来是可以超脱进制进行计算的，而纸带感觉确实是少了一维度，真正的人工智能应是建立在矩阵上，就像Chatgpt那样一层一层的。

1.2九九乘法表的应用

        都说了算即是存，存即是算，那不用一下，显得我就不那么科学了，目标是用上面的九九乘法表去完成运算，但乘法的基础是加法，所以用了方便，先要实现十进制的加法表和十进制的乘法表，用Excel例出，如下所示：

加法表及九九乘法表

        这样就有了图表，可以将其转换成数组用于计算，这里用C++程序简单演示一下，所以上述逻辑可以得：

#include <iostream>
#include <vector>
#include <string.h>
using namespace std;
const int OFFSET=48;

int DSUM[10][10] = {
		{0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
        {1, 2, 3, 4, 5, 6, 7, 8, 9, 0},
        {2, 3, 4, 5, 6, 7, 8, 9, 0, 1},
        {3, 4, 5, 6, 7, 8, 9, 0, 1, 2},
        {4, 5, 6, 7, 8, 9, 0, 1, 2, 3},
        {5, 6, 7, 8, 9, 0, 1, 2, 3, 4},
        {6, 7, 8, 9, 0, 1, 2, 3, 4, 5},
        {7, 8, 9, 0, 1, 2, 3, 4, 5, 6},
        {8, 9, 0, 1, 2, 3, 4, 5, 6, 7},
        {9, 0, 1, 2, 3, 4, 5, 6, 7, 8}
    };
 int DCOMS[10][10] = {
 		{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0, 0, 0, 0, 1, 1},
        {0, 0, 0, 0, 0, 0, 0, 1, 1, 1},
        {0, 0, 0, 0, 0, 0, 1, 1, 1, 1},
        {0, 0, 0, 0, 0, 1, 1, 1, 1, 1},
        {0, 0, 0, 0, 1, 1, 1, 1, 1, 1},
        {0, 0, 0, 1, 1, 1, 1, 1, 1, 1},
        {0, 0, 1, 1, 1, 1, 1, 1, 1, 1},
        {0, 1, 1, 1, 1, 1, 1, 1, 1, 1}
     };  
     
     
int DMULSUM[10][10] = {
		{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
        {0, 2, 4, 6, 8, 0, 2, 4, 6, 8},
        {0, 3, 6, 9, 2, 5, 8, 1, 4, 7},
        {0, 4, 8, 2, 6, 0, 4, 8, 2, 6},
        {0, 5, 0, 5, 0, 5, 0, 5, 0, 5},
        {0, 6, 2, 8, 4, 0, 6, 2, 8, 4},
        {0, 7, 4, 1, 8, 5, 2, 9, 6, 3},
        {0, 8, 6, 4, 2, 0, 8, 6, 4, 2},
        {0, 9, 8, 7, 6, 5, 4, 3, 2, 1}
    };
int DMULCOMS[10][10] = {
		{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 1, 1, 1, 1, 1},
        {0, 0, 0, 0, 1, 1, 1, 2, 2, 2},
        {0, 0, 0, 1, 1, 2, 2, 2, 3, 3},
        {0, 0, 1, 1, 2, 2, 3, 3, 4, 4},
        {0, 0, 1, 1, 2, 3, 3, 4, 4, 5},
        {0, 0, 1, 2, 2, 3, 4, 4, 5, 6},
        {0, 0, 1, 2, 3, 4, 4, 5, 6, 7},
        {0, 0, 1, 2, 3, 4, 5, 6, 7, 8}
    };



// 逐位加法
string decimalAdder(string str1,string str2){
	// 找到最大长度
	size_t maxLength = max(str1.length(), str2.length());
	// 填充短的字符串
	str1 = string(maxLength - str1.length(), '0') + str1;
	str2 = string(maxLength - str2.length(), '0') + str2;
	//创建result存结果
	string result(maxLength, '0');
	int preCarry=0;
	int nowCarry = 0;
	int preSum=0;
	int nowSum=0;

	cout<<str1<<endl<<"+"<<endl<<str2<<endl<<"="<<endl;
	// 从最低位到最高位逐位处理
	for (int i = maxLength - 1; i >= 0; --i) {
	    int a = str1[i] - OFFSET;
	    int b = str2[i] - OFFSET;
		//自身相加位
		preSum= DSUM[a][b];
		
		//更新为最终加和位的值
		nowSum=DSUM[preCarry][preSum];
		//更新为最终进位位的值（9+4+1/8+1+1/9+0+1）
		//（自身进位）或（前面进位与自身和preSum）有进位都行
		nowCarry = DCOMS[a][b] || DCOMS[preCarry][preSum];
		
		//更新前一位的进位结果
		preCarry=nowCarry;
		result[i] = OFFSET +nowSum;
		//cout<<nowSum<<":"<<nowCarry<<endl;
	}

	// 处理最后的进位
	if (preCarry!=0) result = "1" + result;
	return result;
}


// 并位加法(先计算出全部进位，硬件上叫先行进位法)
string decimalParallelAdder(string str1,string str2){
	// 找到最大长度
	size_t maxLength = max(str1.length(), str2.length());
	// 填充短的字符串
	str1 = string(maxLength - str1.length(), '0') + str1;
	str2 = string(maxLength - str2.length(), '0') + str2;
	// 创建进位数组
	int carryArry[maxLength + 1] = {0};
	// 创建result存结果
	string returnResult(maxLength, '0');
	
	int preCarry=0;
	int nowSum=0;
	//cout<<str1<<endl<<"+"<<endl<<str2<<endl<<"="<<endl;
	// 从最低位到最高位逐位处理
	for (int i = maxLength - 1; i >= 0; --i) {
	    int a = str1[i] - OFFSET;
	    int b = str2[i] - OFFSET;
		preCarry = DCOMS[a][b] || DCOMS[preCarry][DSUM[a][b]];
		//提前算出全部进位
		carryArry[i]=preCarry;
	}
	// 进位偏置相加得到结果
	for (int i = 0; i <maxLength; ++i) {
	    int a = str1[i] - OFFSET;
	    int b = str2[i] - OFFSET;
		preCarry=carryArry[i+1];
		nowSum=DSUM[preCarry][DSUM[a][b]];
		returnResult[i]=OFFSET +nowSum;
	}
	//处理进位
	if(carryArry[0]==1)returnResult="1"+returnResult;
	return returnResult;
}



//执行单位的乘法
string toRunMultiply(string str,char c,size_t maxLength){
	//创建result存结果
	string sumResult(maxLength + 1, '0');
	string carryResult(maxLength + 1, '0');
	
    int a = 0;
    int b = c-OFFSET;
	for(int i=0;i<str.length();i++){
		a=str[i]-OFFSET;
		sumResult[i+1]=OFFSET + DMULSUM[a][b];
		carryResult[i]=OFFSET + DMULCOMS[a][b];
	}
	
	return decimalParallelAdder(sumResult,carryResult);
}

// 逐位乘法
string decimalMultiply(string str1,string str2){
	bool isMax=(str1.length()> str2.length());
	string maxString=isMax?str1:str2;
	string minString=isMax?str2:str1;
	int minLength=minString.length()-1;
	string returnResult="";
	vector<string> stringArray;
	//每一位乘法
	for(int i=0;i<minString.length();++i){
		returnResult=toRunMultiply(maxString,minString[minLength-i],maxString.length());
		returnResult = returnResult+string(i, '0');
		stringArray.push_back(returnResult);
	}
	//将所以结果，累加到一起
	for (size_t i =0; i <stringArray.size()-1; ++i) {
		returnResult=decimalParallelAdder(stringArray[i],returnResult);
	}
	//去掉最前面的0
	if(returnResult[0] == '0')returnResult.erase(0, 1); 
	
	return returnResult;
}




int main()
{
	cout<<decimalMultiply("12345","157")<<endl;
	//cout<<decimalParallelAdder("8945121","46548121")<<endl;
	//cout<<decimalAdder("123","9")<<endl;
	//cout<<(8945121+46548121);
    return 0;
}

        So，你说这个有什么用？靠北了，真的是太逊了，你不觉得它可以用来算加法及九九乘法，不是太酷了吗？So,这个有什么用？好吧，还是有一点用处的，比如它可以算超大整形的加法运算及乘法运算，用的也是模拟人用十进制来运算的逻辑，当然无独有偶的，也用人想用这原理弄硬件的十进制计算机，好像投了十几万进去，有一定可行性，能不能商用就是另外一会事了，就像三进制计算机，如果没有好的技术性出来，商业应用遥遥无期，这里超级大数运算的网站，同样可以算连long类型都无法表示的数据，如下所示：

1.3加法的并行性讨论

        上面的乘法结果是正确的，而乘法的函数又用到了加法函数，所以都是正确运算的，当然超级大的数可以用算法可以加速，而不一定用上面的方法，只是提供一个思路，用十进制模拟逻辑门及九九乘法来完成运算，而加法运算能不能并行呢？

        答案是可以，但又不可以。你这个是什么鬼答案，答了跟没答似的，别急先理解一下并行计算，如果将一次加法运算，比喻成蚕丝被的制作过程，那就会有养蚕、剥茧、抽丝，制布等过程，一系列过程后，最终才是蚕丝被的制作，并行就是可以将复杂任务，分成多个简单任务，同时进行处理的过程，而有些步骤只能串行执行，并不能同时执行的。

        就像刚开始，没有蚕丝就不能弄蚕丝被，先决条件定死了，没有前面的进位，那后面的进位就算不出来，那不说加法无法并行计算，事实并非如此，一个加法运算完全并行做不到，但可以部分并行计算，如：超前进位加法器，它就是用空间来换时间，也就说在电路上，它提前算出加法的所以进位位，然后再去计算和就快多了，就像是工厂提前制作好的零件，直接组装就行了，而进位的计算就是串行了，但求和最后又是并行的，所以答案是可以，但又不可以，为了更方便理解，我还写了个按层相加程序，如下所示：

#include <iostream>
#include <vector>
#include <string.h>
using namespace std;
const int OFFSET=48;

int DSUM[10][10] = {
		{0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
        {1, 2, 3, 4, 5, 6, 7, 8, 9, 0},
        {2, 3, 4, 5, 6, 7, 8, 9, 0, 1},
        {3, 4, 5, 6, 7, 8, 9, 0, 1, 2},
        {4, 5, 6, 7, 8, 9, 0, 1, 2, 3},
        {5, 6, 7, 8, 9, 0, 1, 2, 3, 4},
        {6, 7, 8, 9, 0, 1, 2, 3, 4, 5},
        {7, 8, 9, 0, 1, 2, 3, 4, 5, 6},
        {8, 9, 0, 1, 2, 3, 4, 5, 6, 7},
        {9, 0, 1, 2, 3, 4, 5, 6, 7, 8}
    };
 int DCOMS[10][10] = {
 		{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0, 0, 0, 0, 1, 1},
        {0, 0, 0, 0, 0, 0, 0, 1, 1, 1},
        {0, 0, 0, 0, 0, 0, 1, 1, 1, 1},
        {0, 0, 0, 0, 0, 1, 1, 1, 1, 1},
        {0, 0, 0, 0, 1, 1, 1, 1, 1, 1},
        {0, 0, 0, 1, 1, 1, 1, 1, 1, 1},
        {0, 0, 1, 1, 1, 1, 1, 1, 1, 1},
        {0, 1, 1, 1, 1, 1, 1, 1, 1, 1}
     };  
int DOR[2][2]={
	{0,1},
	{1,1}	
};

const int inputSize=6;  
int inputArry[inputSize]={1,8,3,9,1,9};
//int inputArry[inputSize]={1,8,3,7,1,9};


int modifyArray[inputSize+1]={0,0,0,0,0,0,0};


int a,b,c,d,e,f;
void Chuhua();
void printArray(const int arr[], int size);
int reSum(int input1,int input2);
int reCOMS(int input1,int input2);
void reFirLayer(int* arr);
void reSecLayer(int* arr);
void reThrLayer(int* arr);


int main()
{
	Chuhua();
	cout<<a<<":"<<b<<":"<<c<<":"<<d<<":"<<e<<":"<<f<<endl;
	//转换全部
	reFirLayer(modifyArray);
	//算出全部进位
	reSecLayer(modifyArray);
	
	
	//出结果前4位(183+919=1102)
	reThrLayer(modifyArray);
	printArray(modifyArray,inputSize+1);
    return 0;
}

void Chuhua(){
	a=inputArry[0];
	b=inputArry[1];
	c=inputArry[2];
	d=inputArry[3];
	e=inputArry[4];
	f=inputArry[5];
}
void printArray(const int arr[], int size) {
    for(int i = 0; i < size; ++i) {
        cout << "Element at index " << i << " : " << arr[i] << endl;
    }
}
int reSum(int input1,int input2){
	return DSUM[input1][input2];
}
int reCOMS(int input1,int input2){
	return DCOMS[input1][input2];
}
void reFirLayer(int* arr){
	arr[1]=reSum(a,d);
	arr[2]=reSum(b,e);
	arr[3]=reSum(c,f);
	arr[4]=reCOMS(a,d);
	arr[5]=reCOMS(b,e);
	arr[6]=reCOMS(c,f);
}
void reSecLayer(int* arr){
	//这里确实不能并行，只能串行，从最底位开始
	arr[6]=
	DOR[arr[6]][reCOMS(arr[3],0)];	
	arr[5]=
	DOR[arr[5]][reCOMS(arr[2],arr[6])];
	arr[4]=
	DOR[arr[4]][reCOMS(arr[1],arr[5])];
}
void reThrLayer(int * arr){
	arr[0]=reSum(arr[0],arr[4]);
	arr[1]=reSum(arr[1],arr[5]);
	arr[2]=reSum(arr[2],arr[6]);
	arr[3]=reSum(arr[3],0);
}

2、矩阵计算机

        这只是个猜想，矩阵计算机：算即是存，存即是算。一切数据的运算，都是矩阵的不断变化，且会超脱进制限制，可模拟任何的方式的运算，它核心思想就是不断的查矩阵，获取新的值输送到另一个矩阵中，硬件上结合Gpu及高效存储的方式，这种运算过程更加接近人脑的运算过程，也是目前人工智能的基本盘，感觉很离谱但也很神奇，一种新的架构，是在图灵他老人家定义上的一次扩展，更有着并行计算、分布式计算的特点，这就矩阵计算机。

2.1矩阵数据的输入

       数据都为矩阵，为了简便就使用数组来运算，输入的数据当然也要转换成数组，转换方法有两种：一个是分成相同的n个矩阵、还有就是合成一个更大的矩阵，最高位为左上角，最低位为右下角，像一个弓形一样读取与写入，可视为输入单位，如下所示：

2.2矩阵状态转换存储器

        可以理解为固定死的数组，不像是chatGpt那样，可以反向调整权重，这是一种预先编好的转换表，就跟上面的九九乘法表运算差不多，这个矩阵是固定下来的，只可以读的，然后根据地址输出相应的值，用一个或多个矩阵放入读取，结果用新的矩阵存起来，这样就形成了运算的过程，它是超脱了进制限制，所以也试平衡三进制加法吧，如下所示：

平衡三进制半加器真值表

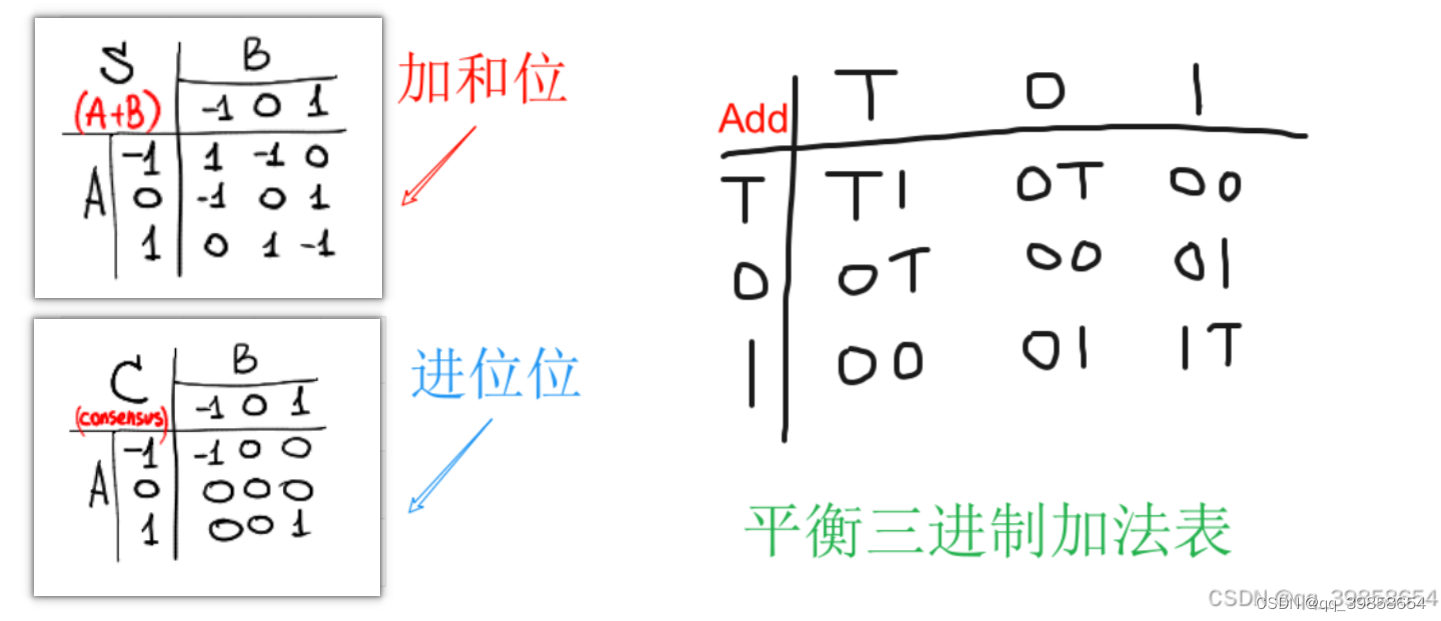
        当然，平衡三进制有T、0、1，而T代表-1，而数组是从0开始的，不能以-1开始，所以这是个问题，不能-1开始，那也没问题，思维足够抽象，现在不要将0、1、2看成数字，只看成是字符，用映射的方法，也就是T/0/1变成0/1/2，而T映射为2，所以调整一下次序，就可以得到相同效果，如下所示：

        电路中可以用2个平衡三进制半加器及1个调和门，组成一个平衡三进制全加器，而这里更简捷了，直接用一个3维数组就行了，平衡三进制全加器27种结果，如下所示：

        用上述方法，直接模拟逻辑门，简捷而高效的实现，只要用2个数组的，就可轻松完成平衡三进制加法运算，代码如下所示：

#include <iostream>
#include <string.h>
using namespace std;
char balanceIndex[3] = {'0','1','T'};

int TSUM[3][3] = {
        {0, 1, 2},
        {1, 2, 0},
        {2, 0, 1}
    };
int TCOMS[3][3] = {
        {0, 0, 0},
        {0, 1, 0},
        {0, 0, 2}
    };

int TFULLSUM[3][3][3] = {
	{
		{0,1,2},
		{1,2,0},
		{2,0,1}
	},
	{
		{1,2,0},
		{2,0,1},
		{0,1,2}
	},
	{
		{2,0,1},
		{0,1,2},
		{1,2,0}
	}
};

int TFULLCOMS[3][3][3] = {
	{
		{0,0,0},
		{0,1,0},
		{0,0,2}
	},
	{
		{0,1,0},
		{1,1,0},
		{0,0,0}
	},
	{
		{0,0,2},
		{0,0,0},
		{2,0,2}
	}
};

int charToInt(char c){
	switch (c) {
		case '0':return 0;
		case '1':return 1;
		case 'T':return 2;
	}
	return -1;
}


// 并位加法
string ternaryParallelAdder(string str1,string str2){
	// 找到最大长度
	size_t maxLength = max(str1.length(), str2.length());
	// 填充短的字符串
	str1 = string(maxLength - str1.length(), '0') + str1;
	str2 = string(maxLength - str2.length(), '0') + str2;
	// 创建进位数组
	int carryArry[maxLength + 1] = {0};
	// 创建result存结果
	string returnResult(maxLength, '0');
	
	
	int preCarry=0;
	int nowSum=0;
	cout<<str1<<endl<<"+"<<endl<<str2<<endl<<"="<<endl;
	// 从最低位到最高位逐位处理
	for (int i = maxLength - 1; i >= 0; --i) {
	    int a = charToInt(str1[i]);
	    int b = charToInt(str2[i]);
	    preCarry=TFULLCOMS[preCarry][a][b];
		//提前算出全部进位，进位计算只能串行计算，
		//前面1位依靠后面1位的计算结果进行
		carryArry[i]=preCarry;
	}
	
	// 进位偏置相加得到结果
	for (int i = 0; i <maxLength; ++i) {
		int a = charToInt(str1[i]);
		int b = charToInt(str2[i]);
		preCarry=carryArry[i+1];
		nowSum=TFULLSUM[preCarry][a][b];
		returnResult[i]=balanceIndex[nowSum];
	}
	//添加进位
	if(carryArry[0]!=0)returnResult=balanceIndex[carryArry[0]]+ returnResult;
	
	return returnResult;
}


int main()
{
	cout<<ternaryParallelAdder("1111","11TT");
	//cout<<ternaryParallelAdder("T11","T11");
    return 0;
}

        都说了，超脱进制限制，那二进制的运算也是可以用行，先上个二进制全加器真值，也就是用个2*2*2的数组就行了，如下所示：

代码如下：

#include <iostream>
#include <string.h>
using namespace std;
const int OFFSET=48;
char binaryIndex[2] = {'0','1'};

int BFULLSUM[2][2][2] = {
	{
		{0,1},
		{1,0}
	},
	{
		{1,0},
		{0,1}
	}
};
int BFULLCOMS[2][2][2] = {
	{
		{0,0},
		{0,1}
	},
	{
		{0,1},
		{1,1}
	}
};

// 并位加法
string binaryParallelAdder(string str1,string str2){
	// 找到最大长度
	size_t maxLength = max(str1.length(), str2.length());
	// 填充短的字符串
	str1 = string(maxLength - str1.length(), '0') + str1;
	str2 = string(maxLength - str2.length(), '0') + str2;
	// 创建进位数组
	int carryArry[maxLength + 1] = {0};
	// 创建result存结果
	string returnResult(maxLength, '0');
	
	int preCarry=0;
	int nowSum=0;
	cout<<str1<<endl<<"+"<<endl<<str2<<endl<<"="<<endl;
	// 从最低位到最高位逐位处理
	for (int i = maxLength - 1; i >= 0; --i) {
	    int a = str1[i]-OFFSET;
	    int b = str2[i]-OFFSET;
	    //提前算出全部进位，进位计算只能串行计算，
	    preCarry=BFULLCOMS[preCarry][a][b];
		//前面1位依靠后面1位的计算结果进行
		carryArry[i]=preCarry;
	}
	
	// 进位偏置相加得到结果
	for (int i = 0; i <maxLength; ++i) {
	    int a = str1[i]-OFFSET;
	    int b = str2[i]-OFFSET;
		preCarry=carryArry[i+1];
		nowSum=BFULLSUM[preCarry][a][b];
		returnResult[i]=binaryIndex[nowSum];
	}
	//添加进位
	if(carryArry[0]!=0)returnResult="1"+ returnResult;
	
	return returnResult;
}


int main()
{

	cout<<binaryParallelAdder("111111000111111","11110011111111");
    return 0;
}

2.3矩阵状态寄存器

        上面的矩阵状态转换存储器，感觉像是ERom，也就是固定死的，或者说是可以编程的多维数组，但有个离谱的猜想，能不能用Mysql或Redis，来实现嵌套表格实现运算什么的，想想都离谱，说有个家伙有我那建了个表，然后不断访问就完成它的计算，或者说也不用建了个表，直接随机访问，只要知道每次返回的值是固定的，将它弄成地址表，不断的访问，用来完成计算，这方法就很离谱了，有一定可能性，这属于是间隔“借”算力的离谱操作了，而这矩阵状态寄存器，是像内存Ram断电没数据，用来存中间运算数据，要永久保存则要运到硬盘或其它机器上，这就是它的大概实现了。


 

结语：

用这种存算一体的结构，感觉就很适合分布式计算及并行计算，结合一下GPU的并行，存算一体式构想，弄出一个在Gpu上跑或是像Redis那样在内存中跑的机器，或者说弄出一台什么进制都能跑的机器来，会不会很流弊，真是想想让人都兴奋呢！

批语：理想很美好，现实很骨感。。、

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1970366.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

企业差旅支出“降本增效”CFO避坑指南之三—— 仅凭一单，更换差旅供应商？

企业差旅支出“降本增效”CFO避坑指南之三—— 仅凭一单，更换差旅供应商？

在企业运营过程中&#xff0c;差旅支出是CFO们需要精细管理的重要成本项。然而&#xff0c;许多中小企业在商旅供应商的选择上&#xff0c;往往容易陷入“仅凭一单价格高&#xff0c;即更换差旅供应商”的误区。这种做法忽视了商旅市场的复杂性和多样性&#xff0c;可能导致企业…
阅读更多...
通过 Python脚本，实现字体文件otf，ttf文件大小的减少

通过 Python脚本，实现字体文件otf，ttf文件大小的减少

FontTools 是一个用于操作字体文件的 Python 库。它支持多种字体格式&#xff0c;包括 TrueType (TTF) 和 OpenType (OTF)&#xff0c;并提供功能来编辑、合并、子集化和生成字体文件 前提&#xff1a;安装了 Python 1、安装 fonttools 库 pip3 install fonttools2、编写脚本…
阅读更多...
Qt项目——文本编辑器（功能模块④）

Qt项目——文本编辑器（功能模块④）

项目地址&#xff1a;GitHub - Outlier9/CatEditor: Cat文本编辑器--Qt 有帮助的话各位点点 star 啦&#xff0c;感谢&#xff01; 如果有需要学习该项目的人&#xff0c;觉得看文档较为困难&#xff0c;可以加我联系方式&#xff0c;给github点个star后可免费提供学习视频&…
阅读更多...
颠覆虚拟试衣行业标准！阿里发布OutfitAnyone：任意服装+任意人！

颠覆虚拟试衣行业标准！阿里发布OutfitAnyone：任意服装+任意人！

文章链接&#xff1a;https://arxiv.org/pdf/2407.16224 git链接:https://humanaigc.github.io/outfit-anyone/ huggingface: https://huggingface.co/spaces/HumanAIGC/OutfitAnyone 亮点直击 顶尖逼真度&#xff1a;OutfitAnyone 方法为虚拟试穿设立了新的行业标准&#xff0…
阅读更多...
【Redis 进阶】持久化（RDB AOF）

【Redis 进阶】持久化（RDB AOF）

Redis&#xff08;数据存储在内存中&#xff09;支持 RDB 和 AOF 两种持久化&#xff08;和 MySQL 里的持久性是一回事&#xff0c;把数据存储在硬盘上&#xff0c;重启进程 / 主机后数据仍然存在 —— 持久&#xff1b;把数据存储在内存上&#xff0c;重启进程 / 主机后数据消…
阅读更多...
夏日清凉体验：气膜体育馆的运动之乐—轻空间

夏日清凉体验：气膜体育馆的运动之乐—轻空间

夏季的酷热常常让人们望而却步&#xff0c;尤其是对于热爱运动的人来说&#xff0c;寻找一个凉爽舒适的运动场所显得尤为重要。气膜体育馆因其独特的建筑特点和环境控制系统&#xff0c;成为了炎炎夏日里篮球、羽毛球等运动项目的理想场地。轻空间将探讨在气膜体育馆内运动的独…
阅读更多...
活动报道 | 盘古信息携IMS OS+小快轻准产品集亮相东莞市中小数转试点供需对接会

活动报道 | 盘古信息携IMS OS+小快轻准产品集亮相东莞市中小数转试点供需对接会

8月1日&#xff0c;由东莞市工业和信息化局主办&#xff0c;南城街道经济发展局承办&#xff0c;东莞市软件行业协会协办的东莞市中小企业数字化转型城市试点供需对接会&#xff08;城区和水乡新城片区&#xff09;隆重召开。市工业和信息化局副局长江小敏、市工业和信息化局信…
阅读更多...
揭秘 CPU 是如何执行计算机指令的

揭秘 CPU 是如何执行计算机指令的

1 CPU 内部逻辑结构 之前的文章《揭秘代码是如何变成机器码的》&#xff0c;其中说到&#xff0c;如果从软件的角度来讲&#xff0c;CPU 就是一个执行各种计算机指令&#xff08;Instruction Code&#xff09;的逻辑机器。 那么这个逻辑机器内部是什么样的&#xff1f;又是如…
阅读更多...
寥寥数笔，动画自成！阿里Tora: 首个轨迹引导的DiT创新实现精确运动控制视频生成

寥寥数笔，动画自成！阿里Tora: 首个轨迹引导的DiT创新实现精确运动控制视频生成

论文链接&#xff1a;https://arxiv.org/pdf/2407.21705 项目链接&#xff1a;https://ali-videoai.github.io/tora_video/ 亮点直击 本文引入了Tora&#xff0c;这是第一个轨迹导向的DiT用于视频生成。如下图2所示&#xff0c;Tora无缝整合了广泛的视觉和轨迹指令&#xff0c;…
阅读更多...
数据挖掘实战-基于Prophet时间序列模型预测阿里巴巴股票价格趋势（文末送书）

数据挖掘实战-基于Prophet时间序列模型预测阿里巴巴股票价格趋势（文末送书）

&#x1f935;‍♂️ 个人主页&#xff1a;艾派森的个人主页 ✍&#x1f3fb;作者简介&#xff1a;Python学习者 &#x1f40b; 希望大家多多支持&#xff0c;我们一起进步&#xff01;&#x1f604; 如果文章对你有帮助的话&#xff0c; 欢迎评论 &#x1f4ac;点赞&#x1f4…
阅读更多...
【系统架构设计师】二十三、通信系统架构设计理论与实践①

【系统架构设计师】二十三、通信系统架构设计理论与实践①

目录 一、通信系统网络架构 1.1 局域网网络架构 1.1.1 单核心架构 1.1.2 双核心架构 1.1.3 环型架构 1.1.4 层次型架构 1.2 广域网网络架构 1.2.1 单核心广域网 1.2.2 双核心广域网 1.2.3 环型广域网 1.2.4 半冗余广域网 1.2.5 对等子域广域网 1.2.6 层次子域架构…
阅读更多...
文献阅读：基于拓扑结构模型构建ICI收益诊断模型

文献阅读：基于拓扑结构模型构建ICI收益诊断模型

介绍 Custom scoring based on ecological topology of gut microbiota associated with cancer immunotherapy outcome是来自法国Gustave Roussy Cancer Campus的Laurence Zitvogel实验室最近发表在cell的关于使用肠道微生物拓扑结构预测免疫治疗疗效的文章。 该研究提供基于…
阅读更多...
html+css 实现左平移背景按钮

html+css 实现左平移背景按钮

前言&#xff1a;哈喽&#xff0c;大家好&#xff0c;今天给大家分享htmlcss 绚丽效果&#xff01;并提供具体代码帮助大家深入理解&#xff0c;彻底掌握&#xff01;创作不易&#xff0c;如果能帮助到大家或者给大家一些灵感和启发&#xff0c;欢迎收藏关注哦 &#x1f495; 文…
阅读更多...
【Android Studio】gradle文件、配置、版本下载、国内源（gradle版本以及gradle-plugin版本）

【Android Studio】gradle文件、配置、版本下载、国内源（gradle版本以及gradle-plugin版本）

文章目录 AS查看gradle-plugin版本及gradle版本&#xff08;图形&#xff09;查看gradle-plugin版本及gradle版本&#xff08;配置文件&#xff09;配置文件分析解决gradle下载失败、版本错乱等问题。 AS查看gradle-plugin版本及gradle版本&#xff08;图形&#xff09; 查看gr…
阅读更多...
金航标萨科微总经理宋仕强介绍金航标热售产品

金航标萨科微总经理宋仕强介绍金航标热售产品

金航标萨科微slkor总经理宋仕强介绍说&#xff0c;金航标kinghelm热售产品型号有&#xff0c;金航标胶壳(线对板/线对线)连接器KH-VH-2P-ZK、KH-VH-5P-ZK、KH-VH-4P-ZK、KH-A2557-2X07Y&#xff0c;金航标kinghelm&#xff08;www.kinghelm.com.cn&#xff09;的弹簧片/弹片有K…
阅读更多...
“田野八式”与人类学的田野研究方法

“田野八式”与人类学的田野研究方法

作 者&#xff1a;赵旭东 来 源&#xff1a;《民族学刊》 &#xff3b;摘要&#xff3d; 笔者根据自己多年来的田野工作经验&#xff0c;将人类学田野研究方法总结为: 心存异趣、扎实描记、留心古旧、知微知彰、知柔知刚、神游冥想、克己宽容以及文字天下八个方面&#xff0c…
阅读更多...
3百题英语四级听力考试练习题ACCESS\EXCEL数据库

3百题英语四级听力考试练习题ACCESS\EXCEL数据库

其实一直都想搞一搞英语听力题相关的数据&#xff0c;但是一直都没有遇到过或者遇到过但是没办法弄下来&#xff0c;今天有幸遇到一个英语四级听力考试练习题&#xff0c;听力MP3文件包含96个&#xff0c;题目包含300题&#xff0c;具体请查看截图&#xff0c;截图包含了所有字…
阅读更多...
笔记小结：《利用Python进行数据分析》之读取数据

笔记小结：《利用Python进行数据分析》之读取数据

目录 读取文本格式的数据 基本操作 指定分隔符 指定标题行 层次化索引 使用正则表达式分隔 跳过某些行 缺失值处理 逐块读取文本文件 设置显示的最大行数 只读取几行 逐块读取文件 将数据写出到文本格式 基本操作 使用其它分隔符 使用其它标记符标记空白字符串 禁…
阅读更多...
IoTDB 入门教程 企业篇①——IoTDB企业版(TimechoDB)快速上手

IoTDB 入门教程 企业篇①——IoTDB企业版(TimechoDB)快速上手

文章目录 一、前文二、试用三、解压四、激活五、启动六、连接七、停止八、IoTDB-Workbench 一、前文 IoTDB入门教程——导读 二、试用 通过天谋科技官网&#xff0c;联系天谋科技的商务。请求免费试用TimechoDB企业版&#xff0c;获得试用软件包 三、解压 iotdb-enterprise…
阅读更多...
舞蹈症宝贝的专属锻炼秘籍来啦～✨

舞蹈症宝贝的专属锻炼秘籍来啦～✨

嘿宝贝们&#xff01;&#x1f44b; 是不是有时候觉得身体里的“小舞蹈家”总想出来蹦跶两下&#xff0c;但又怕锻炼不当反而“跳”出问题&#xff1f;别怕&#xff0c;今天就给你种草一套超萌又超有效的舞蹈症患者锻炼大法&#xff01;&#x1f389; &#x1f31f;【热身小妖精…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023