原文链接：https://www.cnblogs.com/aksoam/p/18279394
更多精彩，关注博客园主页，不断学习！不断进步！

我的主页

csdn很少看私信，有事请b站私信

博客园主页-发文字笔记-常用

有限元鹰的主页 内容：

1. ABAQUS数值模拟相关
2. Python科学计算
3. 开源框架，编程学习笔记

哔哩哔哩主页-发视频-常用

FE-有限元鹰的个人空间 内容：

1. 模拟案例
2. 网格划分
3. 游戏视频，及其他搬运视频

5. 高斯公式(Gauss formula)

考虑带权函数的求积公式:

$$I[f]={\int }_a^b\rho (x)f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_{i}f(x_i)\text{\hspace{1em}(7)}$$

其中函数 $\rho (x)>0$ 为已知函数 , 称为权函数.

定义:若对于节点 $x_i$ ∈ [a,b] 及求积系数 ${\omega }_i$ , 求积公式(7)的代数精度为 2n+1, 则称节点 $x_i$ 为高斯点 , ${\omega }_i$ 为高斯系数 , 相应的求积公式 (7) 称为带权的高斯公式

高斯公式可看成是 f(x) 用高斯点上的n次插值多项式代替所得积分值 . 下面给出了确定高斯点的一种求解方法

定理5.5.2 $x_i$ (i = 0,1,··· ,n) 是求积公式 (7) 的高斯点的充分必要条件是 : 多项式 $\Pi (x)={\prod }_{i=0}^n(x-x_i)$ 与任意次数不超过 n 的多项式 q(x) 关于权函数 ρ(x) 正交:
$${\int }_a^b\rho (x)\Pi (x)q(x)\mathrm{d}x=0.$$

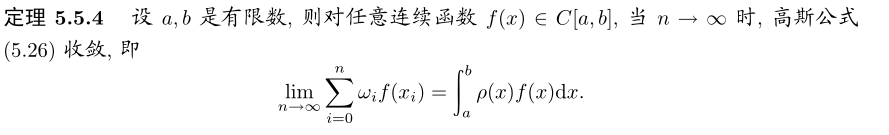
5.1 常用的高斯型公式

$$I[f]={\int }_a^b\rho (x)f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_{i}f(x_i)\text{\hspace{1em}(7)}$$

高斯 – 勒让德公式

令 $\rho (x)\equiv 1,[a,b]=[-1,1]$ ,此时关于权函数 $\rho (x)=1$ 的区间 [−1,1] 上的正交多项式为勒让德 (Legendre) 正交多项式.

n=0时:

$${\int }_{-1}^{1}f(x)\mathrm{d}x\approx 2f(0),$$

n=1时:

$${\int }_{-1}^{1}f(x)\mathrm{d}x\approx f\left(-\frac{1}{\sqrt{3}}\right)+f\left(\frac{1}{\sqrt{3}}\right).$$

n=2时:

$${\int }_{-1}^{1}f(x)\mathrm{d}x\approx \frac{5}{9}f\left(-\sqrt{\frac{3}{5}}\right)+\frac{8}{9}f(0)+\frac{5}{9}f\left(\sqrt{\frac{3}{5}}\right).$$

对于一般区间[a,b]的积分,需要先变换积分区间,然后使用高斯-勒让德公式计算.

$$x=\frac{a+b}{2}+\frac{b-a}{2}t$$

$${\int }_a^{b}f(x)\mathrm{d}x=\frac{b-a}{2}{\int }_{-1}^{1}f\left(\frac{a+b}{2}+\frac{b-a}{2}t\right)\mathrm{d}t.$$

$${\int }_a^{b}f(x)\mathrm{d}x\approx \frac{b-a}{2}\sum _{i=0}^n{\omega }_{i}f\left(\frac{a+b}{2}+\frac{b-a}{2}{x}_i\right),$$

其中, ${\omega }_i$ 为高斯系数, $x_i$ 为高斯点.

常用的高斯点及高斯系数表:

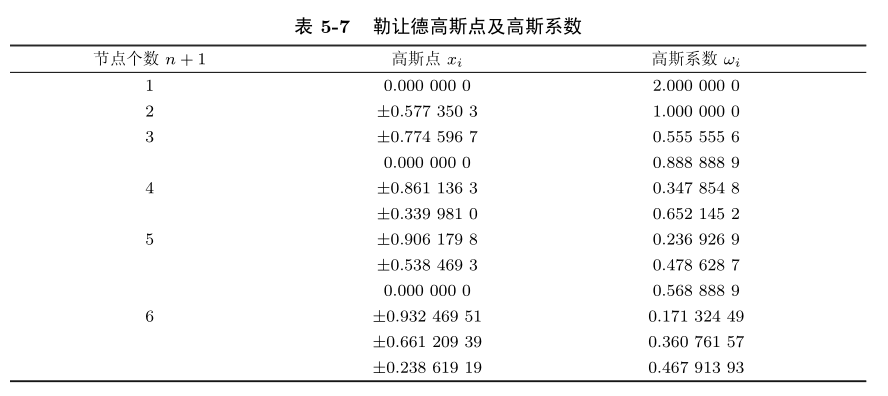
高斯 – 切比雪夫公式

令 $\rho (x)=\frac{1}{\sqrt{1-x^2}},[a,b]=[-1,1].$,高斯点$x_i$分布和对应高斯系数${\omega }_i$为:

$$x_i=\cos \frac{2i+1}{2(n+1)}\pi ,i=0,1,\cdots ,n.$$

$${\omega }_i=\frac{\pi }{n+1}.$$

积分区间为[-1,+1]的高斯–切比雪夫公式为:

$${\int }_{-1}^1\frac{1}{\sqrt{1-x^2}}f(x)\mathrm{d}x\approx \frac{\pi }{n+1}\sum _{i=0}^{n}f\left(\cos \frac{2i+1}{2(n+1)}\pi \right).$$

n=2时:

$${\int }_{-1}^1\frac{1}{\sqrt{1-x^2}}f(x)\mathrm{d}x\approx \frac{\pi }{3}\left[f\left(-\frac{\sqrt{3}}{2}\right)+f(0)+f\left(\frac{\sqrt{3}}{2}\right)\right].$$

高斯 – 拉盖尔公式

令 $\rho (x)={\mathrm{e}}^{-x},[a,b]=[0,\infty ).$ 此时高斯系数为:

$${\omega }_i=\frac{x_i}{L_{n+2}^2(x_i)},i=0,1,\cdots ,n.$$

高斯 – 拉盖尔积分公式为:

$${\int }_0^{\infty }{\mathrm{e}}^{-x}f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_{i}f(x)$$

n=0时:

$${\int }_0^{\infty }{\mathrm{e}}^{-x}f(x)\mathrm{d}x\approx f(1).$$

n=1时:

$${\int }_0^{\infty }{\mathrm{e}}^{-x}f(x)\mathrm{d}x\approx \frac{2+\sqrt{2}}{4}f(2-\sqrt{2})+\frac{2-\sqrt{2}}{4}f(2+\sqrt{2}).$$

n=2,3,4时的高斯点和高斯系数:

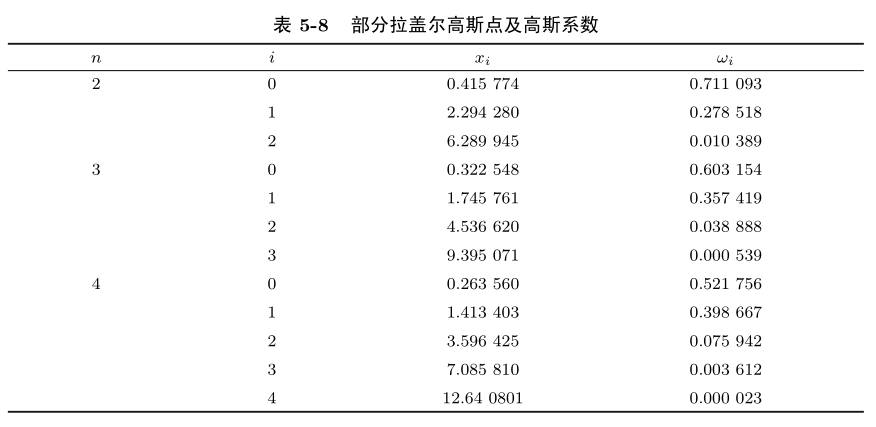
• 公式变换

对于形如 ${\int }_{\alpha }^{\infty }{\mathrm{e}}^{-\beta x}f(x)\mathrm{d}x(\beta >0)$ 的积分,需要转换为标准高斯-拉盖尔公式的形式:

$$x=\frac{1}{\beta }t+\alpha$$

$$\begin{array}{rl}{\int }_{\alpha }^{\infty }{\mathrm{e}}^{-\beta x}f(x)\mathrm{d}x& =\frac{1}{\beta }{\mathrm{e}}^{-\alpha \beta }{\int }_0^{\infty }{\mathrm{e}}^{-t}f\left(\frac{1}{\beta }t+\alpha \right)\mathrm{d}t\\ & \approx \frac{1}{\beta }{\mathrm{e}}^{-\alpha \beta }\sum _{i=0}^n{\omega }_{i}f\left(\frac{x_i}{\beta }+\alpha \right).\end{array}$$

对于形如 ${\int }_0^{\infty }g(x)\mathrm{d}x$ 的积分,首先确保g(x)是收敛的,其次需要转换为标准高斯-拉盖尔公式的形式:

$$\begin{array}{c}{\int }_0^{\infty }g(x)\mathrm{d}x={\int }_0^{\infty }{\mathrm{e}}^{-x}f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_{i}f(x_i)\\ =\sum _{i=0}^n{\omega }_i{\mathrm{e}}^{x_i}g(x_i).\end{array}$$

高斯 – 埃尔米特 (Gauss-Hermite) 公式

令 $\rho (x)={\mathrm{e}}^{-x^2},[a,b]=(-\infty ,+\infty ).$ ,高斯点为n+1次埃尔米特正交多项式 $H_{n+1}(x)$ 的零点, 对应高斯系数为:

$${\omega }_i=\frac{2^{n+2}(n+1)!\sqrt{\pi }}{{\left[H_{n+2}(x_i)\right]}^2},i=0,1,\cdots ,n.$$

此时求积公式为:

$${\int }_{-\infty }^{+\infty }{\mathrm{e}}^{-x^2}f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_{i}f(x_i),$$

n = 1 时的高斯 – 埃尔米特公式为

$${\int }_{-\infty }^{+\infty }{\mathrm{e}}^{-x^2}f(x)\mathrm{d}x\approx \frac{\sqrt{\pi }}{2}f\left(-\frac{\sqrt{2}}{2}\right)+\frac{\sqrt{\pi }}{2}f\left(\frac{\sqrt{2}}{2}\right).$$

n = 2 时的高斯 – 埃尔米特公式为

$${\int }_{-\infty }^{+\infty }{\mathrm{e}}^{-x^2}f(x)\mathrm{d}x\approx \frac{\sqrt{\pi }}{6}f\left(-\frac{\sqrt{6}}{2}\right)+\frac{2\sqrt{\pi }}{3}f(0)+\frac{\sqrt{\pi }}{6}f\left(\frac{\sqrt{6}}{2}\right)$$

高斯 – 埃尔米特公式的另一形式如下,g(x)需要保证广义积分收敛性:

$${\int }_{-\infty }^{+\infty }g(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_i{\mathrm{e}}^{x_i^2}g(x_i).$$

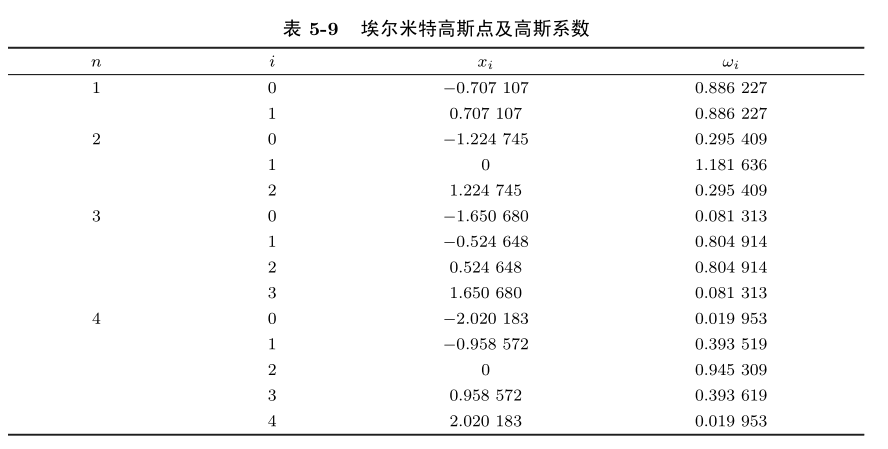
5.2 高斯积分的应用

几种积分的python实现

def Integ1dGuassLegendre(f, a:float=-1, b:float=1, n:int=5)->float:
    """给定积分区间[a,b]和高斯积分点个数n,计算一维高斯-勒让德积分公式"""
    # 计算勒让德-高斯积分点及权重
    roots, weights = legendre_gauss_points_and_weights(n)
    if a==-1 and b==1:
        # 标准型积分
        result=sum([wi*f(xi) for xi,wi in zip(roots,weights)])
        return result
    else:
        # 非标准型积分, 需变换积分区间
        t= lambda x: 0.5*(b-a)*x+0.5*(b+a)
        result=0.5*(b-a)*sum([wi*f(t(xi)) for xi,wi in zip(roots,weights)])
        return result

def legendre_gauss_points_and_weights(n:int)->Tuple[List[float],List[float]]:
    """给定高斯点个数n,计算[-1,+1]内的勒让德-高斯积分点及权重"""
    import scipy.special as sp
    # 计算勒让德多项式的根（即高斯点）
    roots, weights = sp.roots_legendre(n)
    # sp.roots_legendre函数会返回勒让德多项式的根（即高斯点）及其对应的高斯系数。
    return roots, weights

def Integ1dGuassHermite(f,n:int=3,Is_standard:bool=True)->float:
    """给定n(>=1)值,积分范围[-inf,+inf],计算一维高斯-埃尔米特积分"""
    # 计算埃尔米特-高斯积分点及权重
    if n<=0:
        raise ValueError("高斯-埃尔米特积分时,n必须大于0")
    print(f"积分点个数: {n+1}, 积分范围: [-inf,+inf]")
    roots, weights = gauss_hermite_points_and_weights(n+1)
    if Is_standard:
        # 为标准型积分
        result=sum([wi*f(xi) for xi,wi in zip(roots,weights)])
        return result
    else:
        # 计算 \int_{-inf}^{+inf} g(x) dx
        result=sum([wi*np.exp(xi**2)*f(xi) for xi,wi in zip(roots,weights)])
        return result

def gauss_hermite_points_and_weights(n:int)->Tuple[List[float],List[float]]:
    """给定高斯点个数n,计算[-inf,+inf]内的埃尔米特-高斯积分点及权重"""
    import scipy.special as sp
    # 计算埃尔米特多项式的根（即高斯点）及其对应的高斯系数
    roots, weights = sp.roots_hermite(n)
    return roots, weights

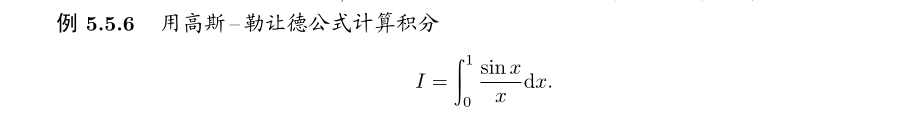
• Answer:

f3=lambda x: np.sin(x)/x if x!=0 else 1
from formu_lib import *
# 积分范围
a,b=0,1

# 计算积分
r1=VarStepInteg1d(f3,a,b,1e-7,method=2)

# 使用高斯勒让德方法计算积分
r2=Integ1dGuassLegendre(f3,a,b)

print(f"复化梯形积分：{r1}")
print(f"高斯勒让德积分：{r2}")

showError(r1,0.9460831)
showError(r2,0.9460831)

# 输出:
# 复化梯形积分：0.9460830464324462
# 高斯勒让德积分：0.9460830703672151
# 数值解: 0.9460830464324462, 精确解: 0.9460831, 误差: 5.662034733111406e-08
# 数值解: 0.9460830703672151, 精确解: 0.9460831, 误差: 3.132154553076945e-08

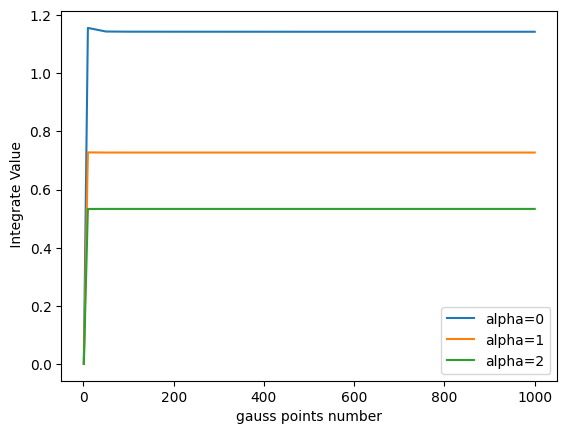
• Answer:

def f4(alpha:int):
    return lambda x: abs(x)**(alpha+0.75)

a,b=-1,1

r={}
n=[1,10,50,100,500,1000]
for alpha in [0,1,2]:
    re=[]
    for ni in n:
        re.append(Integ1dGuassLegendre(f4(alpha=alpha),a,b,ni))
    r[alpha]=re

from matplotlib import pyplot as plt
for alpha in [0,1,2]:
    plt.plot(n,r[alpha],label=f"alpha={alpha}")
plt.xlabel('gauss points number')
plt.ylabel(' Integrate Value')
plt.legend()
plt.show()

• Answer:

# %%
# 例题5.5.8
from formu_lib import *
f5=lambda x: np.cos(x)

result=Integ1dGuassHermite(f5,5)
showError(result, 1.3803884470)

# 积分点个数: 5, 积分范围: [-inf,+inf]
# 数值解: 1.3803900759356564, 精确解: 1.380388447, 误差: -1.1800559906898897e-06

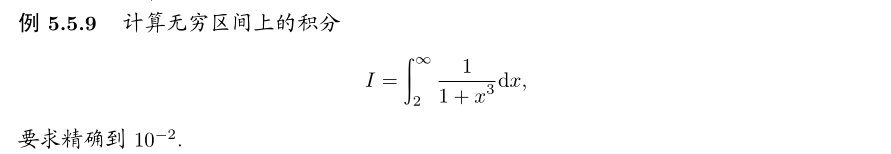
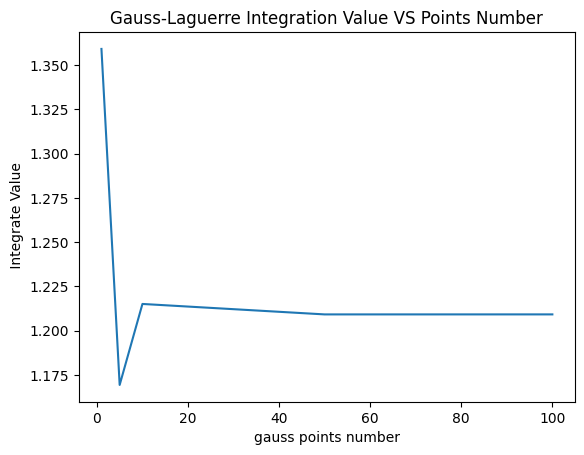
• Answer:

# %%
# 例题5.5.9
from formu_lib import *
g=lambda x: 1/(1+x**3)
n=[1,5,10,50,100]
result=[Integ1dGuassLaguerre(g,ni,beta=0) for ni in n]
print(f"广义积分结果：{result}")
# 广义积分结果：1.1693599387646283
from matplotlib import pyplot as plt

plt.plot(n,result)
plt.xlabel('gauss points number')
plt.ylabel(' Integrate Value')
plt.title('Gauss-Laguerre Integration Value VS Points Number')
plt.show()
# 收敛于1.2091