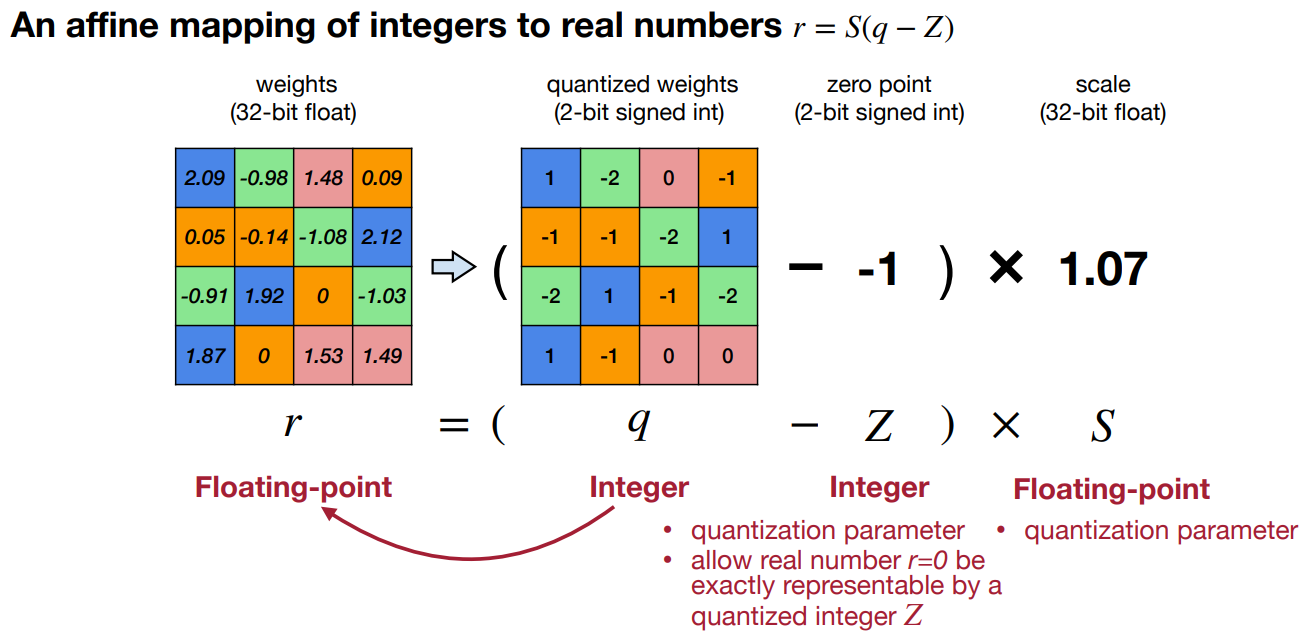
什么是线性量化
r
=
S
(
q
−
Z
)
r = S(q - Z)
r=S(q−Z)
式中,
S
S
S是比例因子,通常是一个浮点数;
q
q
q是
r
r
r的量化后的表示,是一个整数;
Z
Z
Z也是一个整数,把
q
q
q中和
Z
Z
Z相同的整数映射到
r
r
r中零,因此
Z
Z
Z是零点偏移。
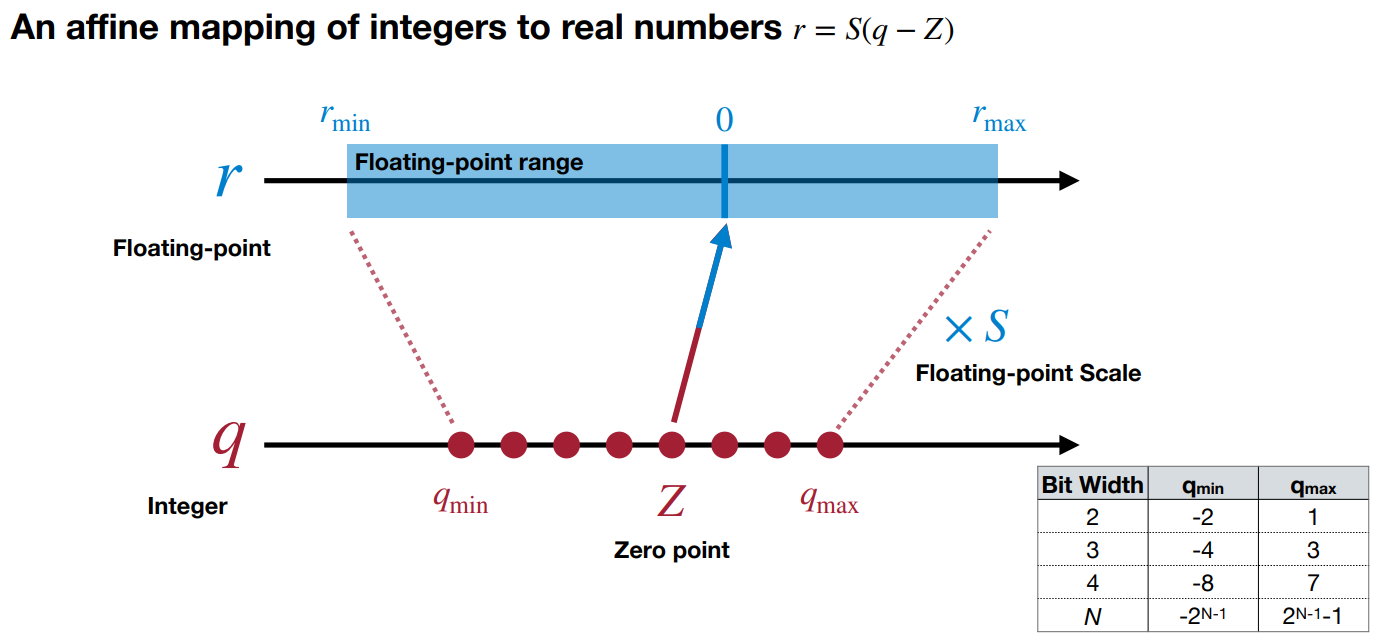
如何确定参数
让
r
m
i
n
,
r
m
a
x
r_{min}, r_{max}
rmin,rmax为所有原始权重的最小值和最大值;让
q
m
i
n
,
q
m
a
x
q_{min}, q_{max}
qmin,qmax为量化范围的最小值和最大值(一般为
2
n
,
2
n
−
1
2^n, 2^n-1
2n,2n−1,对于某个
n
n
n)。那么,可以得到
r
m
i
n
=
S
(
q
m
i
n
−
Z
)
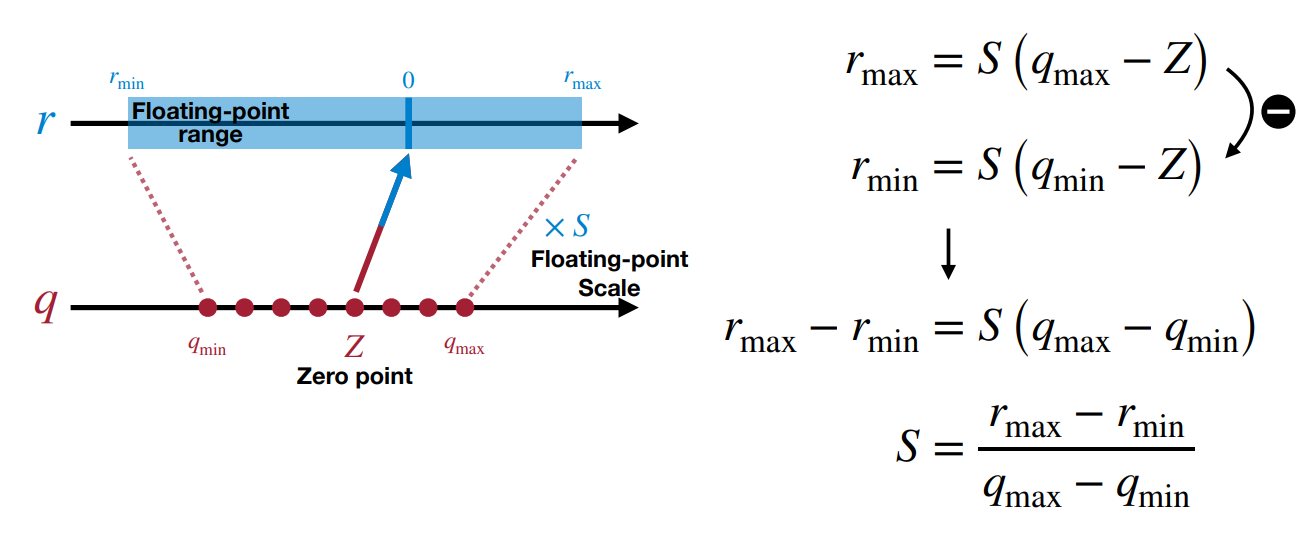
r_{min} = S(q_{min} - Z)
rmin=S(qmin−Z)和
r
m
a
x
=
S
(
q
m
a
x
−
Z
)
r_{max} = S(q_{max} - Z)
rmax=S(qmax−Z)。第一项减去第二项,可以得到
r
m
a
x
−
r
m
i
n
=
S
(
q
m
a
x
−
q
m
i
n
)
r_{max} - r_{min} = S(q_{max} - q_{min})
rmax−rmin=S(qmax−qmin),即
S
=
r
m
a
x
−
r
m
i
n
q
m
a
x
−
q
m
i
n
S=\frac{r_{max} - r_{min}}{q_{max} - q_{min}}
S=qmax−qminrmax−rmin
对于零点偏移,我们希望我们的量化方案能够准确表示零点。因此,尽管从公式
r
m
i
n
=
S
(
q
m
i
n
−
Z
)
r_{min} = S(q_{min} - Z)
rmin=S(qmin−Z)来看,我们可以得到
Z
=
q
m
i
n
−
r
m
i
n
S
Z = q_{min} - \frac{r_{min}}{S}
Z=qmin−Srmin,从这个式子上看,有可能
Z
Z
Z不是整数,因此我们将其改为
Z
=
round
(
q
m
i
n
−
r
m
i
n
S
)
Z = \text{round}\left(q_{min} - \frac{r_{min}}{S}\right)
Z=round(qmin−Srmin)。
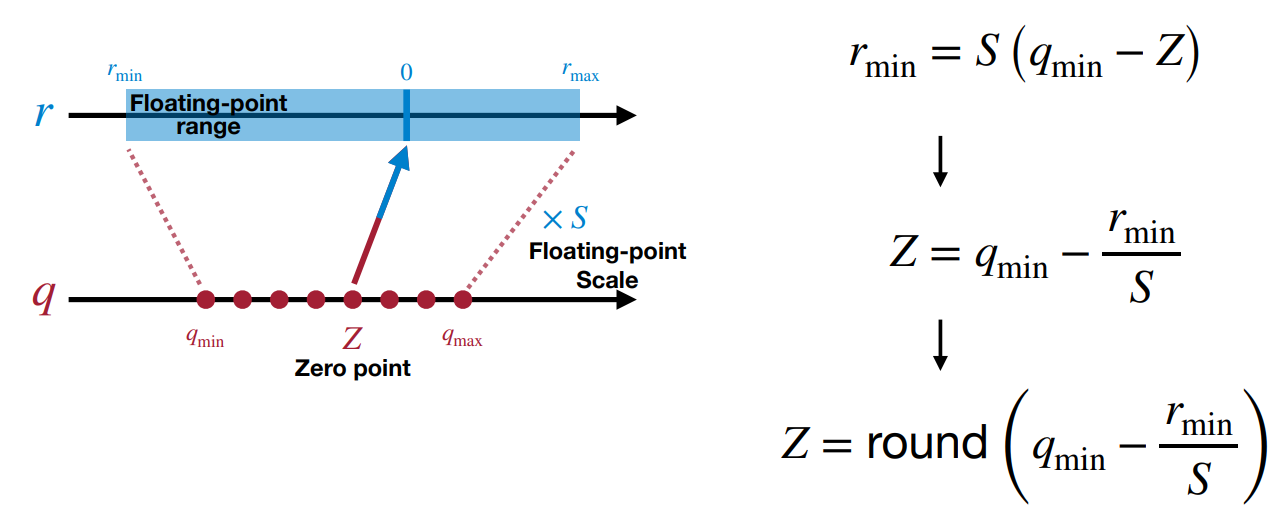
非对称 VS 对称

左边是非对称量化,因其可代表的正负值之间的不对称性而得名。
右边是对称量化,在这种情况下, Z Z Z的值固定为 0 0 0,则比例因子 S = ∣ r ∣ m a x q m i n S = \frac{\lvert r \rvert_{max}}{q_{min}} S=qmin∣r∣max。虽然实现起来比较容易,处理零的逻辑也比较干净,但这导致量化范围被有效地浪费了(也就是说,有一系列的值可以用我们的方案来表示,但不需要);这在任何ReLU操作之后尤其如此,我们知道这些值将是非负的,这实质上失去了一整点信息。一般来说,这意味着我们不使用这个方案来量化激活,但我们可以用来量化权重。
量化推理(Quantized Inference)
线性量化的矩阵乘法(Linear Quantized Matrix Multiplication)
r
=
S
(
q
−
Z
)
r = S(q - Z)
r=S(q−Z)
上式子中,
q
q
q是
r
r
r的量化后的表示,根据这个映射关系对矩阵乘法进行替换
Y = W X Y = WX Y=WX
S Y ( q Y − Z Y ) = S W ( q W − z W ) ⋅ S X ( q X − Z x ) S_Y(q_Y - Z_Y) = S_W(q_W - z_W) \cdot S_X(q_X - Z_x) SY(qY−ZY)=SW(qW−zW)⋅SX(qX−Zx)
从而得到线性量化的矩阵乘法,如下所示:
q Y = S W S X S Y ( q W − z W ) ( q X − Z X ) + Z Y q_Y = \frac{S_WS_X}{S_Y}(q_W - z_W)(q_X - Z_X) + Z_Y qY=SYSWSX(qW−zW)(qX−ZX)+ZY
q Y = S W S X S Y ( q W q X − z W q X − Z X q W + Z W Z X ) + Z Y q_Y = \frac{S_WS_X}{S_Y}(q_Wq_X - z_Wq_X - Z_Xq_W + Z_WZ_X) + Z_Y qY=SYSWSX(qWqX−zWqX−ZXqW+ZWZX)+ZY
请注意,
Z
X
q
W
+
Z
W
Z
X
Z_Xq_W + Z_WZ_X
ZXqW+ZWZX可以预先计算,因为这不取决于具体的输入(
Z
X
Z_X
ZX只取决于我们的量化方案);而且,对于对称量化来说,将
Z
W
=
0
Z_W = 0
ZW=0,可以简化为
q
Y
=
S
W
S
X
S
Y
(
q
W
q
X
−
Z
X
q
W
)
+
Z
Y
q_Y = \frac{S_WS_X}{S_Y}(q_Wq_X - Z_Xq_W) + Z_Y
qY=SYSWSX(qWqX−ZXqW)+ZY
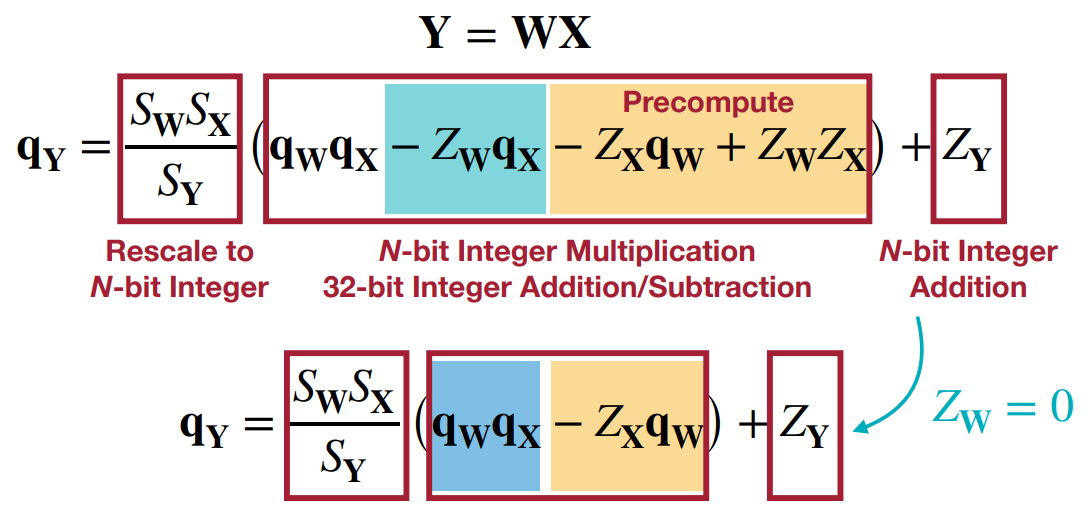
线性量化的全连接层(Linear Quantized Fully-Connected Layer)
在线性量化的矩阵乘法的基础上,添加偏移量 b b b
Y = W X + b Y = WX + b Y=WX+b
S Y ( q Y − Z Y ) = S W ( q W − z W ) ⋅ S X ( q X − Z x ) + S b ( q b − Z b ) S_Y(q_Y - Z_Y) = S_W(q_W - z_W) \cdot S_X(q_X - Z_x) + S_b(q_b - Z_b) SY(qY−ZY)=SW(qW−zW)⋅SX(qX−Zx)+Sb(qb−Zb)
q Y = S W S X S Y ( q W − z W ) ( q X − Z X ) + Z Y + S b S Y ( q b − Z b ) q_Y = \frac{S_WS_X}{S_Y}(q_W - z_W)(q_X - Z_X) + Z_Y + \frac{S_b}{S_Y}(q_b - Z_b) qY=SYSWSX(qW−zW)(qX−ZX)+ZY+SYSb(qb−Zb)
设 S b = S W S X S_b=S_WS_X Sb=SWSX,则可以合并同类项,得
q Y = S W S X S Y ( q W q X − z W q X − Z X q W + Z W Z X + q b − Z b ) + Z Y q_Y = \frac{S_WS_X}{S_Y}(q_Wq_X - z_Wq_X - Z_Xq_W + Z_WZ_X + q_b - Z_b) + Z_Y qY=SYSWSX(qWqX−zWqX−ZXqW+ZWZX+qb−Zb)+ZY
为了使得计算简单,使用线性量化,即令 Z W = 0 Z_W=0 ZW=0和 Z b = 0 Z_b=0 Zb=0,得
q Y = S W S X S Y ( q W q X + q b − Z X q W ) + Z Y q_Y = \frac{S_WS_X}{S_Y}(q_Wq_X + q_b - Z_Xq_W) + Z_Y qY=SYSWSX(qWqX+qb−ZXqW)+ZY
最后,令
q
bias
=
q
b
−
Z
X
q
W
q_{\text{bias}} = q_b - Z_Xq_W
qbias=qb−ZXqW,因为
q
bias
q_{\text{bias}}
qbias可以预先计算,得
q
Y
=
S
W
S
X
S
Y
(
q
W
q
X
+
q
bias
)
+
Z
Y
q_Y = \frac{S_WS_X}{S_Y}(q_Wq_X + q_{\text{bias}}) + Z_Y
qY=SYSWSX(qWqX+qbias)+ZY
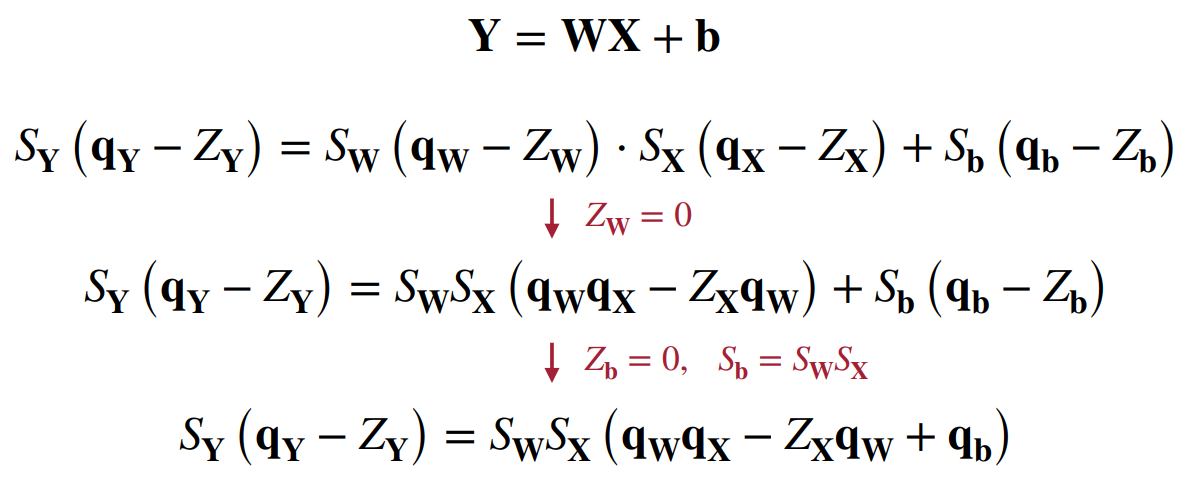
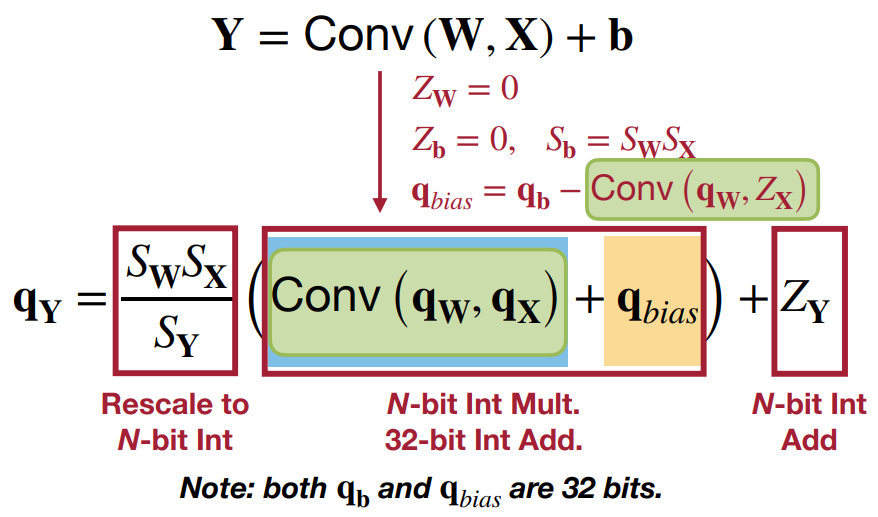
线性量化的卷积层(Linear Quantized Convolution Layer)
事实证明,由于卷积在本质上也是一个线性算子,其量化的推导与线性层的推导极为相似。通过类似的定义(即
Z
W
=
Z
b
=
0
,
S
b
=
S
W
S
X
Z_W=Z_b=0,S_b=S_WS_X
ZW=Zb=0,Sb=SWSX),我们将得到
q
Y
=
S
W
S
X
S
Y
(
Conv
(
q
W
,
q
X
)
+
q
bias
)
+
Z
Y
q_Y = \frac{S_WS_X}{S_Y}\left(\text{Conv}(q_W, q_X) + q_{\text{bias}}\right) + Z_Y
qY=SYSWSX(Conv(qW,qX)+qbias)+ZY
其中,
q
bias
=
q
b
−
Conv
(
q
W
,
Z
X
)
q_{\text{bias}} = q_b - \text{Conv}(q_W, Z_X)
qbias=qb−Conv(qW,ZX)。
总结
通过上面的推导,我们得到了一下线性量化的全连接层和卷积层,因此我们可以把训练好的模型中的所有层都进行线性量化,替换为线性向量化的全连接层和卷积层,从而实现了把模型中的浮点运算替换成整型运算。
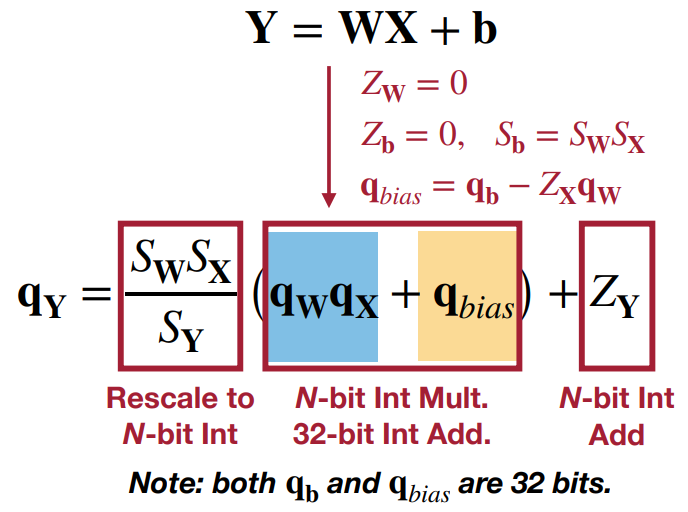
实现
求补码范围: [ − 2 n − 1 , 2 n − 1 − 1 ] [-2^{n-1}, 2^{n-1}-1] [−2n−1,2n−1−1] n-bit
# A *n*-bit signed integer can enode integers in the range $[-2^{n-1}, 2^{n-1}-1]$
def get_quantized_range(bitwidth):
quantized_max = (1 << (bitwidth - 1)) - 1
quantized_min = -(1 << (bitwidth - 1))
return quantized_min, quantized_max
实现线性量化表达式: q = i n t ( r o u n d ( r / S ) ) + Z q = \mathrm{int}(\mathrm{round}(r/S)) + Z q=int(round(r/S))+Z
def linear_quantize(fp_tensor, bitwidth, scale, zero_point, dtype=torch.int8) -> torch.Tensor:
"""
linear quantization for single fp_tensor
from
fp_tensor = (quantized_tensor - zero_point) * scale
we have,
quantized_tensor = int(round(fp_tensor / scale)) + zero_point
:param tensor: [torch.(cuda.)FloatTensor] floating tensor to be quantized
:param bitwidth: [int] quantization bit width
:param scale: [torch.(cuda.)FloatTensor] scaling factor
:param zero_point: [torch.(cuda.)IntTensor] the desired centroid of tensor values
:return:
[torch.(cuda.)FloatTensor] quantized tensor whose values are integers
"""
assert(fp_tensor.dtype == torch.float)
assert(isinstance(scale, float) or
(scale.dtype == torch.float and scale.dim() == fp_tensor.dim()))
assert(isinstance(zero_point, int) or
(zero_point.dtype == dtype and zero_point.dim() == fp_tensor.dim()))
# Step 1: scale the fp_tensor
scaled_tensor = fp_tensor.div(scale)
# Step 2: round the floating value to integer value
rounded_tensor = scaled_tensor.round_()
rounded_tensor = rounded_tensor.to(dtype)
# Step 3: shift the rounded_tensor to make zero_point 0
shifted_tensor = rounded_tensor.add_(zero_point)
# Step 4: clamp the shifted_tensor to lie in bitwidth-bit range
quantized_min, quantized_max = get_quantized_range(bitwidth)
quantized_tensor = shifted_tensor.clamp_(quantized_min, quantized_max)
return quantized_tensor
测试线性量化
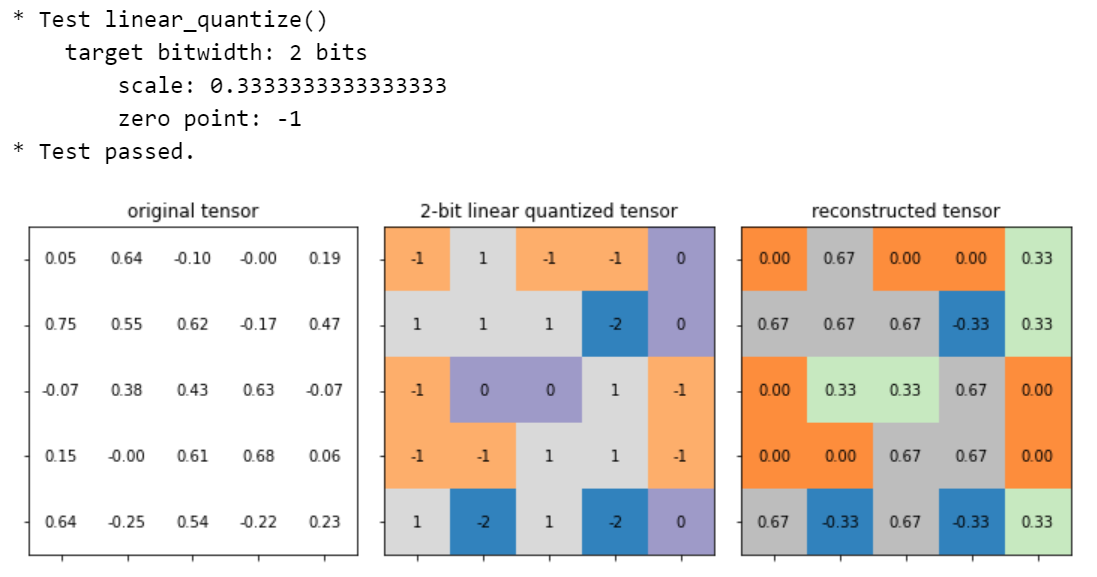
实现参数表达式:
S = ( r m a x − r m i n ) / ( q m a x − q m i n ) S=(r_{\mathrm{max}} - r_{\mathrm{min}}) / (q_{\mathrm{max}} - q_{\mathrm{min}}) S=(rmax−rmin)/(qmax−qmin)
Z = i n t ( r o u n d ( q m i n − r m i n / S ) ) Z = \mathrm{int}(\mathrm{round}(q_{\mathrm{min}} - r_{\mathrm{min}} / S)) Z=int(round(qmin−rmin/S))
def get_quantization_scale_and_zero_point(fp_tensor, bitwidth):
"""
get quantization scale for single tensor
:param fp_tensor: [torch.(cuda.)Tensor] floating tensor to be quantized
:param bitwidth: [int] quantization bit width
:return:
[float] scale
[int] zero_point
"""
quantized_min, quantized_max = get_quantized_range(bitwidth)
fp_max = fp_tensor.max().item()
fp_min = fp_tensor.min().item()
scale = (fp_max - fp_min) / (quantized_max - quantized_min)
zero_point = quantized_min - fp_min / scale
# clip the zero_point to fall in [quantized_min, quantized_max]
if zero_point < quantized_min:
zero_point = quantized_min
elif zero_point > quantized_max:
zero_point = quantized_max
else: # convert from float to int using round()
zero_point = round(zero_point)
return scale, int(zero_point)
把线性量化表达式和参数表达式封装在一个函数里
def linear_quantize_feature(fp_tensor, bitwidth):
"""
linear quantization for feature tensor
:param fp_tensor: [torch.(cuda.)Tensor] floating feature to be quantized
:param bitwidth: [int] quantization bit width
:return:
[torch.(cuda.)Tensor] quantized tensor
[float] scale
[int] zero_point
"""
scale, zero_point = get_quantization_scale_and_zero_point(fp_tensor, bitwidth)
quantized_tensor = linear_quantize(fp_tensor, bitwidth, scale, zero_point)
return quantized_tensor, scale, zero_point
上述的实现是非对称量化,接下来,我们实现对称量化。
Z = 0 Z=0 Z=0
r m a x = S ⋅ q m a x r_{\mathrm{max}} = S \cdot q_{\mathrm{max}} rmax=S⋅qmax
对于对称量化来说,我们只需要根据
r
m
a
x
r_{max}
rmax表达式求出scale,接着调用函数linear_quantize(tensor, bitwidth, scale, zero_point=0)即可。下面是实现
r
m
a
x
r_{max}
rmax表达式:
def get_quantization_scale_for_weight(weight, bitwidth):
"""
get quantization scale for single tensor of weight
:param weight: [torch.(cuda.)Tensor] floating weight to be quantized
:param bitwidth: [integer] quantization bit width
:return:
[floating scalar] scale
"""
# we just assume values in weight are symmetric
# we also always make zero_point 0 for weight
fp_max = max(weight.abs().max().item(), 5e-7)
_, quantized_max = get_quantized_range(bitwidth)
return fp_max / quantized_max
对通道进行对称线性量化
回顾一下,对于二维卷积,权重张量是一个四维张量,形状为(num_output_channels, num_input_channels, kernel_height, kernel_width)。
实验表明,对不同的输出通道使用不同的缩放系数 S S S和零点 Z Z Z会有更好的表现。因此,对于非对称量化,我们必须为每个输出通道的子张量确定缩放因子 S S S和零点 Z Z Z;对于对称量化,则只需确定缩放因子 S S S即可。下面是使用对称量化来对每个通道进行线性量化。
def linear_quantize_weight_per_channel(tensor, bitwidth):
"""
linear quantization for weight tensor
using different scales and zero_points for different output channels
:param tensor: [torch.(cuda.)Tensor] floating weight to be quantized
:param bitwidth: [int] quantization bit width
:return:
[torch.(cuda.)Tensor] quantized tensor
[torch.(cuda.)Tensor] scale tensor
[int] zero point (which is always 0)
"""
dim_output_channels = 0
num_output_channels = tensor.shape[dim_output_channels]
scale = torch.zeros(num_output_channels, device=tensor.device)
for oc in range(num_output_channels):
_subtensor = tensor.select(dim_output_channels, oc)
_scale = get_quantization_scale_for_weight(_subtensor, bitwidth)
scale[oc] = _scale
scale_shape = [1] * tensor.dim()
scale_shape[dim_output_channels] = -1
scale = scale.view(scale_shape)
quantized_tensor = linear_quantize(tensor, bitwidth, scale, zero_point=0)
return quantized_tensor, scale, 0
量化前
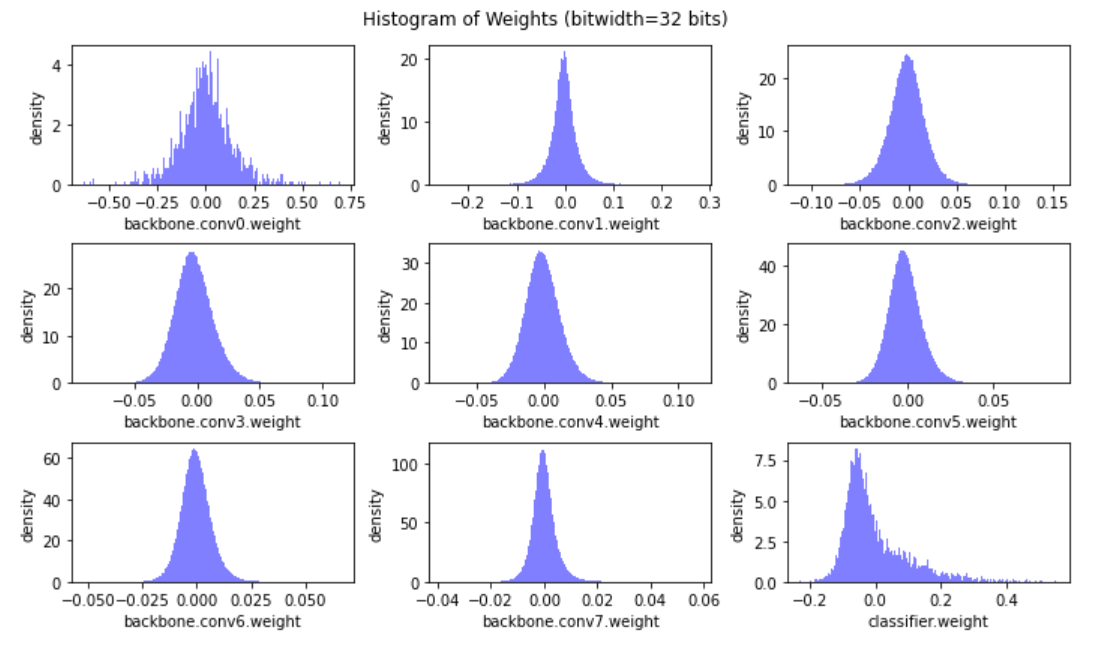
量化后
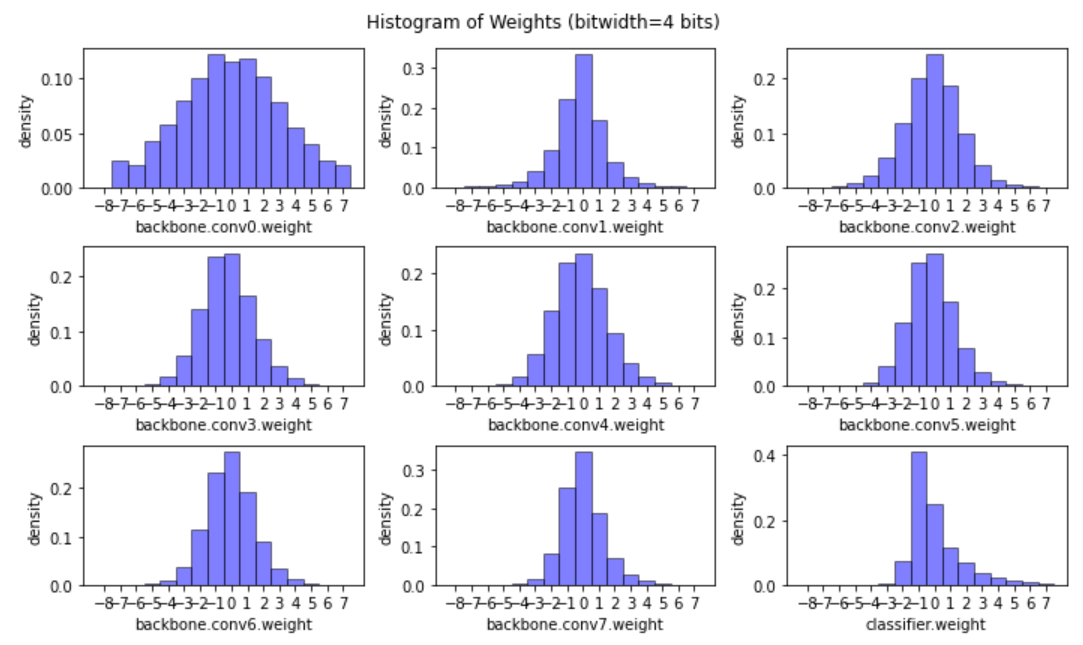
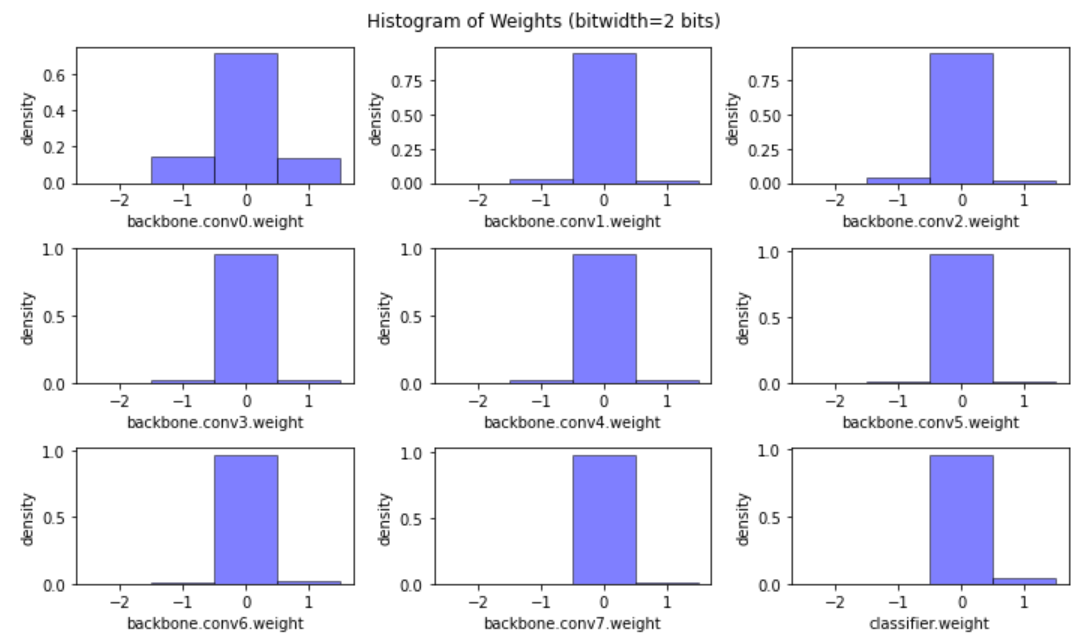
对全连接层进行量化
要实现对bias进行对称线性量化,首先要求出 S b i a s S_{\mathrm{bias}} Sbias
Z b i a s = 0 Z_{\mathrm{bias}} = 0 Zbias=0
S b i a s = S w e i g h t ⋅ S i n p u t S_{\mathrm{bias}} = S_{\mathrm{weight}} \cdot S_{\mathrm{input}} Sbias=Sweight⋅Sinput
def linear_quantize_bias_per_output_channel(bias, weight_scale, input_scale):
"""
linear quantization for single bias tensor
quantized_bias = fp_bias / bias_scale
:param bias: [torch.FloatTensor] bias weight to be quantized
:param weight_scale: [float or torch.FloatTensor] weight scale tensor
:param input_scale: [float] input scale
:return:
[torch.IntTensor] quantized bias tensor
"""
assert(bias.dim() == 1)
assert(bias.dtype == torch.float)
assert(isinstance(input_scale, float))
if isinstance(weight_scale, torch.Tensor):
assert(weight_scale.dtype == torch.float)
weight_scale = weight_scale.view(-1)
assert(bias.numel() == weight_scale.numel())
bias_scale = weight_scale * input_scale
quantized_bias = linear_quantize(bias, 32, bias_scale,
zero_point=0, dtype=torch.int32)
return quantized_bias, bias_scale, 0
对于量化全连接层来说,要预先计算 Q b i a s Q_{\mathrm{bias}} Qbias
Q b i a s = q b i a s − L i n e a r [ Z i n p u t , q w e i g h t ] Q_{\mathrm{bias}} = q_{\mathrm{bias}} - \mathrm{Linear}[Z_{\mathrm{input}}, q_{\mathrm{weight}}] Qbias=qbias−Linear[Zinput,qweight]
def shift_quantized_linear_bias(quantized_bias, quantized_weight, input_zero_point):
"""
shift quantized bias to incorporate input_zero_point for nn.Linear
shifted_quantized_bias = quantized_bias - Linear(input_zero_point, quantized_weight)
:param quantized_bias: [torch.IntTensor] quantized bias (torch.int32)
:param quantized_weight: [torch.CharTensor] quantized weight (torch.int8)
:param input_zero_point: [int] input zero point
:return:
[torch.IntTensor] shifted quantized bias tensor
"""
assert(quantized_bias.dtype == torch.int32)
assert(isinstance(input_zero_point, int))
return quantized_bias - quantized_weight.sum(1).to(torch.int32) * input_zero_point
接下来,我们就可以计算量化全连接层的输出了
q o u t p u t = ( L i n e a r [ q i n p u t , q w e i g h t ] + Q b i a s ) ⋅ ( S i n p u t S w e i g h t / S o u t p u t ) + Z o u t p u t q_{\mathrm{output}} = (\mathrm{Linear}[q_{\mathrm{input}}, q_{\mathrm{weight}}] + Q_{\mathrm{bias}})\cdot (S_{\mathrm{input}} S_{\mathrm{weight}} / S_{\mathrm{output}}) + Z_{\mathrm{output}} qoutput=(Linear[qinput,qweight]+Qbias)⋅(SinputSweight/Soutput)+Zoutput
def quantized_linear(input, weight, bias, feature_bitwidth, weight_bitwidth,
input_zero_point, output_zero_point,
input_scale, weight_scale, output_scale):
"""
quantized fully-connected layer
:param input: [torch.CharTensor] quantized input (torch.int8)
:param weight: [torch.CharTensor] quantized weight (torch.int8)
:param bias: [torch.IntTensor] shifted quantized bias or None (torch.int32)
:param feature_bitwidth: [int] quantization bit width of input and output
:param weight_bitwidth: [int] quantization bit width of weight
:param input_zero_point: [int] input zero point
:param output_zero_point: [int] output zero point
:param input_scale: [float] input feature scale
:param weight_scale: [torch.FloatTensor] weight per-channel scale
:param output_scale: [float] output feature scale
:return:
[torch.CharIntTensor] quantized output feature (torch.int8)
"""
assert(input.dtype == torch.int8)
assert(weight.dtype == input.dtype)
assert(bias is None or bias.dtype == torch.int32)
assert(isinstance(input_zero_point, int))
assert(isinstance(output_zero_point, int))
assert(isinstance(input_scale, float))
assert(isinstance(output_scale, float))
assert(weight_scale.dtype == torch.float)
# Step 1: integer-based fully-connected (8-bit multiplication with 32-bit accumulation)
if 'cpu' in input.device.type:
# use 32-b MAC for simplicity
output = torch.nn.functional.linear(input.to(torch.int32), weight.to(torch.int32), bias)
else:
# current version pytorch does not yet support integer-based linear() on GPUs
output = torch.nn.functional.linear(input.float(), weight.float(), bias.float())
# Step 2: scale the output
# hint: 1. scales are floating numbers, we need to convert output to float as well
# 2. the shape of weight scale is [oc, 1, 1, 1] while the shape of output is [batch_size, oc]
output = output.float() * (input_scale * weight_scale / output_scale).view(1, -1)
# Step 3: shift output by output_zero_point
output = output + output_zero_point
# Make sure all value lies in the bitwidth-bit range
output = output.round().clamp(*get_quantized_range(feature_bitwidth)).to(torch.int8)
return output
测试量化全连接层的输出

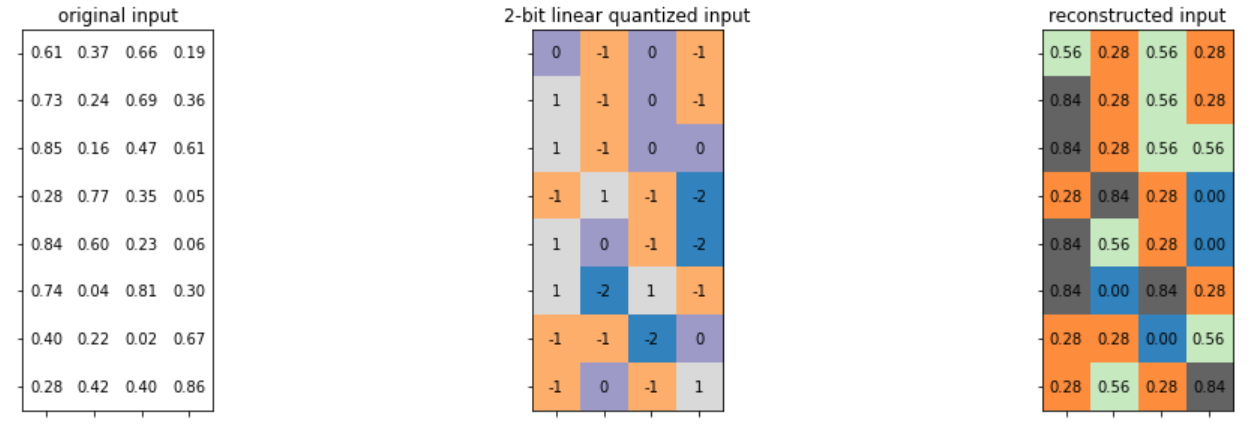
对卷积层进行量化
对于量化卷积层来说,要预先计算 Q b i a s Q_{\mathrm{bias}} Qbias
Q b i a s = q b i a s − C O N V [ Z i n p u t , q w e i g h t ] Q_{\mathrm{bias}} = q_{\mathrm{bias}} - \mathrm{CONV}[Z_{\mathrm{input}}, q_{\mathrm{weight}}] Qbias=qbias−CONV[Zinput,qweight]
def shift_quantized_conv2d_bias(quantized_bias, quantized_weight, input_zero_point):
"""
shift quantized bias to incorporate input_zero_point for nn.Conv2d
shifted_quantized_bias = quantized_bias - Conv(input_zero_point, quantized_weight)
:param quantized_bias: [torch.IntTensor] quantized bias (torch.int32)
:param quantized_weight: [torch.CharTensor] quantized weight (torch.int8)
:param input_zero_point: [int] input zero point
:return:
[torch.IntTensor] shifted quantized bias tensor
"""
assert(quantized_bias.dtype == torch.int32)
assert(isinstance(input_zero_point, int))
return quantized_bias - quantized_weight.sum((1,2,3)).to(torch.int32) * input_zero_point
然后就可以计算量化卷积层的输出了
q o u t p u t = ( C O N V [ q i n p u t , q w e i g h t ] + Q b i a s ) ⋅ ( S i n p u t S w e i g h t / S o u t p u t ) + Z o u t p u t q_{\mathrm{output}} = (\mathrm{CONV}[q_{\mathrm{input}}, q_{\mathrm{weight}}] + Q_{\mathrm{bias}}) \cdot (S_{\mathrm{input}}S_{\mathrm{weight}} / S_{\mathrm{output}}) + Z_{\mathrm{output}} qoutput=(CONV[qinput,qweight]+Qbias)⋅(SinputSweight/Soutput)+Zoutput
def quantized_conv2d(input, weight, bias, feature_bitwidth, weight_bitwidth,
input_zero_point, output_zero_point,
input_scale, weight_scale, output_scale,
stride, padding, dilation, groups):
"""
quantized 2d convolution
:param input: [torch.CharTensor] quantized input (torch.int8)
:param weight: [torch.CharTensor] quantized weight (torch.int8)
:param bias: [torch.IntTensor] shifted quantized bias or None (torch.int32)
:param feature_bitwidth: [int] quantization bit width of input and output
:param weight_bitwidth: [int] quantization bit width of weight
:param input_zero_point: [int] input zero point
:param output_zero_point: [int] output zero point
:param input_scale: [float] input feature scale
:param weight_scale: [torch.FloatTensor] weight per-channel scale
:param output_scale: [float] output feature scale
:return:
[torch.(cuda.)CharTensor] quantized output feature
"""
assert(len(padding) == 4)
assert(input.dtype == torch.int8)
assert(weight.dtype == input.dtype)
assert(bias is None or bias.dtype == torch.int32)
assert(isinstance(input_zero_point, int))
assert(isinstance(output_zero_point, int))
assert(isinstance(input_scale, float))
assert(isinstance(output_scale, float))
assert(weight_scale.dtype == torch.float)
# Step 1: calculate integer-based 2d convolution (8-bit multiplication with 32-bit accumulation)
input = torch.nn.functional.pad(input, padding, 'constant', input_zero_point)
if 'cpu' in input.device.type:
# use 32-b MAC for simplicity
output = torch.nn.functional.conv2d(input.to(torch.int32), weight.to(torch.int32), None, stride, 0, dilation, groups)
else:
# current version pytorch does not yet support integer-based conv2d() on GPUs
output = torch.nn.functional.conv2d(input.float(), weight.float(), None, stride, 0, dilation, groups)
output = output.round().to(torch.int32)
if bias is not None:
output = output + bias.view(1, -1, 1, 1)
# Step 2: scale the output
# hint: 1. scales are floating numbers, we need to convert output to float as well
# 2. the shape of weight scale is [oc, 1, 1, 1] while the shape of output is [batch_size, oc, height, width]
output = output.float() * (input_scale * weight_scale / output_scale).view(1, -1, 1, 1)
# Step 3: shift output by output_zero_point
# hint: one line of code
output = output + output_zero_point
# Make sure all value lies in the bitwidth-bit range
output = output.round().clamp(*get_quantized_range(feature_bitwidth)).to(torch.int8)
return output
对模型进行线性量化
于是,我们可以创建QuantizedConv2d、QuantizedLinear、QuantizedMaxPool2d、QuantizedAvgPool2d对象,使用这些class对模型进行线性量化。
class QuantizedConv2d(nn.Module):
def __init__(self, weight, bias,
input_zero_point, output_zero_point,
input_scale, weight_scale, output_scale,
stride, padding, dilation, groups,
feature_bitwidth=8, weight_bitwidth=8):
super().__init__()
# current version Pytorch does not support IntTensor as nn.Parameter
self.register_buffer('weight', weight)
self.register_buffer('bias', bias)
self.input_zero_point = input_zero_point
self.output_zero_point = output_zero_point
self.input_scale = input_scale
self.register_buffer('weight_scale', weight_scale)
self.output_scale = output_scale
self.stride = stride
self.padding = (padding[1], padding[1], padding[0], padding[0])
self.dilation = dilation
self.groups = groups
self.feature_bitwidth = feature_bitwidth
self.weight_bitwidth = weight_bitwidth
def forward(self, x):
return quantized_conv2d(
x, self.weight, self.bias,
self.feature_bitwidth, self.weight_bitwidth,
self.input_zero_point, self.output_zero_point,
self.input_scale, self.weight_scale, self.output_scale,
self.stride, self.padding, self.dilation, self.groups
)
class QuantizedLinear(nn.Module):
def __init__(self, weight, bias,
input_zero_point, output_zero_point,
input_scale, weight_scale, output_scale,
feature_bitwidth=8, weight_bitwidth=8):
super().__init__()
# current version Pytorch does not support IntTensor as nn.Parameter
self.register_buffer('weight', weight)
self.register_buffer('bias', bias)
self.input_zero_point = input_zero_point
self.output_zero_point = output_zero_point
self.input_scale = input_scale
self.register_buffer('weight_scale', weight_scale)
self.output_scale = output_scale
self.feature_bitwidth = feature_bitwidth
self.weight_bitwidth = weight_bitwidth
def forward(self, x):
return quantized_linear(
x, self.weight, self.bias,
self.feature_bitwidth, self.weight_bitwidth,
self.input_zero_point, self.output_zero_point,
self.input_scale, self.weight_scale, self.output_scale
)
class QuantizedMaxPool2d(nn.MaxPool2d):
def forward(self, x):
# current version PyTorch does not support integer-based MaxPool
return super().forward(x.float()).to(torch.int8)
class QuantizedAvgPool2d(nn.AvgPool2d):
def forward(self, x):
# current version PyTorch does not support integer-based AvgPool
return super().forward(x.float()).to(torch.int8)
对模型进行线性量化
# we use int8 quantization, which is quite popular
feature_bitwidth = weight_bitwidth = 8
quantized_model = copy.deepcopy(model_fused)
quantized_backbone = []
ptr = 0
while ptr < len(quantized_model.backbone):
if isinstance(quantized_model.backbone[ptr], nn.Conv2d) and \
isinstance(quantized_model.backbone[ptr + 1], nn.ReLU):
conv = quantized_model.backbone[ptr]
conv_name = f'backbone.{ptr}'
relu = quantized_model.backbone[ptr + 1]
relu_name = f'backbone.{ptr + 1}'
input_scale, input_zero_point = \
get_quantization_scale_and_zero_point(
input_activation[conv_name], feature_bitwidth)
output_scale, output_zero_point = \
get_quantization_scale_and_zero_point(
output_activation[relu_name], feature_bitwidth)
quantized_weight, weight_scale, weight_zero_point = \
linear_quantize_weight_per_channel(conv.weight.data, weight_bitwidth)
quantized_bias, bias_scale, bias_zero_point = \
linear_quantize_bias_per_output_channel(
conv.bias.data, weight_scale, input_scale)
shifted_quantized_bias = \
shift_quantized_conv2d_bias(quantized_bias, quantized_weight,
input_zero_point)
quantized_conv = QuantizedConv2d(
quantized_weight, shifted_quantized_bias,
input_zero_point, output_zero_point,
input_scale, weight_scale, output_scale,
conv.stride, conv.padding, conv.dilation, conv.groups,
feature_bitwidth=feature_bitwidth, weight_bitwidth=weight_bitwidth
)
quantized_backbone.append(quantized_conv)
ptr += 2
elif isinstance(quantized_model.backbone[ptr], nn.MaxPool2d):
quantized_backbone.append(QuantizedMaxPool2d(
kernel_size=quantized_model.backbone[ptr].kernel_size,
stride=quantized_model.backbone[ptr].stride
))
ptr += 1
elif isinstance(quantized_model.backbone[ptr], nn.AvgPool2d):
quantized_backbone.append(QuantizedAvgPool2d(
kernel_size=quantized_model.backbone[ptr].kernel_size,
stride=quantized_model.backbone[ptr].stride
))
ptr += 1
else:
raise NotImplementedError(type(quantized_model.backbone[ptr])) # should not happen
quantized_model.backbone = nn.Sequential(*quantized_backbone)
# finally, quantized the classifier
fc_name = 'classifier'
fc = model.classifier
input_scale, input_zero_point = \
get_quantization_scale_and_zero_point(
input_activation[fc_name], feature_bitwidth)
output_scale, output_zero_point = \
get_quantization_scale_and_zero_point(
output_activation[fc_name], feature_bitwidth)
quantized_weight, weight_scale, weight_zero_point = \
linear_quantize_weight_per_channel(fc.weight.data, weight_bitwidth)
quantized_bias, bias_scale, bias_zero_point = \
linear_quantize_bias_per_output_channel(
fc.bias.data, weight_scale, input_scale)
shifted_quantized_bias = \
shift_quantized_linear_bias(quantized_bias, quantized_weight,
input_zero_point)
quantized_model.classifier = QuantizedLinear(
quantized_weight, shifted_quantized_bias,
input_zero_point, output_zero_point,
input_scale, weight_scale, output_scale,
feature_bitwidth=feature_bitwidth, weight_bitwidth=weight_bitwidth
)

计算量化后模型的准确率