为什么要拒绝嵌套代码？

news2024/11/15 1:34:40

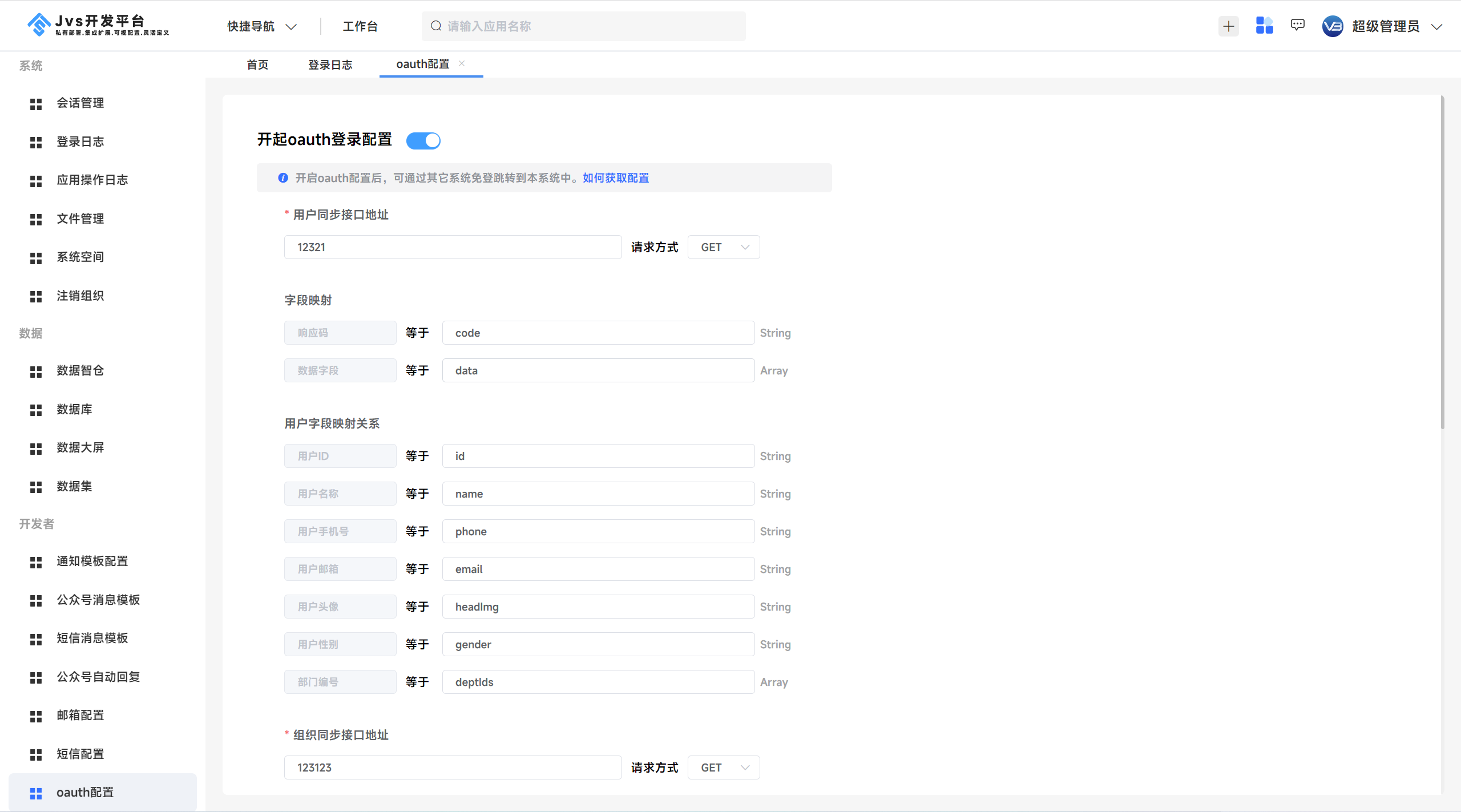
linux 内核的最早作者 linus torvalds 在 linux 内核样式指南第一节中提到：

if you need more than 3 levels of indentation, you’re screwed anyway, and should fix your program.

如果你需要超过3级的缩进，你无论如何都搞砸了，应该修复你的程序。

什么是嵌套

嵌套代码是指您向函数中添加更多的内部块。一般认为，每一个左大括号都为函数增加了一个深度。下面介绍一些例子：

int calculate(int bottom, int top)
{
  return bottom + top;
}

此函数的嵌套深度为 1.

在此基础上再增加一个 if 语句：

int calculate(int bottom, int top)
{
  if (top > bottom)
  {
    return bottom + top;
  }
  else
  {
    return 0;
  }
}

该函数的嵌套深度增加为 2.

如果再增加一个循环：

int calculate(int bottom, int top)
{
  if (top > bottom)
  {
    int sum = 0;
    for (int number = bottom; number <= top; number++)
    {
      sum += number;
    }
    return sum;
  }
  else
  {
    return 0;
  }
}

此时，calculate 函数有三个左大括号，那么我们认为该函数的深度为 3.

许多优秀的工程师都认为，三层嵌套是优秀编程范式的最大深度。

如果超过了三层，那么随之而来的复杂程度将会成倍增加，复杂的函数逻辑将会使阅读和修改变得困难甚至毫无可能。

尤其是在千万行级别的大型工程中，这种毫无制约的嵌套将会是一个定时炸弹！

那么如何重构代码，使其去嵌套化呢？

去嵌套化

我们有两种方式重构代码，使其嵌套深度小于等于 3：提取和反转。这两者结合可以达到我们的目的。

提取是指将复杂函数中的特定部分提取出来，使其成为一个新的函数。

反转是指反转 if 和 else 中的代码块，使其能够提前 return ，继而去除 else 语句，减小嵌套深度。

首先给出一个四层深度的实例代码，此代码在上述 for 循环中增加了一个 if 语句：

int calculate(int bottom, int top)
{ // level one
  if (top > bottom)
  { // level two
    int sum = 0;
    for (int number = bottom; number <= top; number++)
    { // level three
      if (number % 2 == 0)
      { // level four
        sum += number;
      }
    }
    return sum;
  }
  else
  {
    return 0;
  }
}

提取

将 for 循环内部部分提取出来，形成一个单独的函数 filterNumber.

int filterNumber(int number)
{
  if (number % 2 == 0)
  {
    return number;
  }
  return 0;
}

int calculate(int bottom, int top)
{ // level one
  if (top > bottom)
  { // level two
    int sum = 0;
    for (int number = bottom; number <= top; number++)
    { // level three
      sum += filterNumber(number);
    }
    return sum;
  }
  else
  { // level two
    return 0;
  }
}

此时的函数深度为 3.

反转

反转的思路就是，将一些错误判定条件（提前 return，或者抛出异常）放到真正的业务代码前面，这样就可以省略了许多的 else 语句，避免陷入更深的嵌套中。

接下来我们反转 if 和 else 中的语句，并将 if 中的条件取反：

int filterNumber(int number)
{
  if (number % 2 == 0)
  {
    return number;
  }
  return 0;
}

int calculate(int bottom, int top)
{ // level one
  if (top <= bottom)
  { // level two
    return 0;
  }
  else
  { // level two
    int sum = 0;
    for (int number = bottom; number <= top; number++)
    { // level three
      sum += filterNumber(number);
    }
    return sum;
  }
}

实际上容易发现，我们并不需要这个 else 语句块，因为如果满足那个会导致提前return的条件，那么语句将会按照正常顺序执行。所以去掉 else：

int filterNumber(int number)
{
  if (number % 2 == 0)
  {
    return number;
  }
  return 0;
}

int calculate(int bottom, int top)
{ // level one
  if (top <= bottom)
  { // level two
    return 0;
  }
  int sum = 0;
  for (int number = bottom; number <= top; number++)
  { // level two
    sum += filterNumber(number);
  }
  return sum;
}