线性代数篇

news2024/11/15 6:52:29

主线为花书第二章-线性代数，但其上面一些表述属实费解，于是参考B站3Blue1Brown线性代数和B站同济子豪兄的视频讲解。

先放一句3B1B的话共勉，伙计们不要被数学公式吓到，慢慢钻研，慢慢推肯定能学懂。线性代数这一部分相信一般理工科的同志们肯定都学过，这里主要是稍微看看回忆下。

标量、向量、矩阵和张量

标量(scalar)：一个单独的数，用斜体表示，通常被赋予小写的变量名称。

向量(vector)：物理中的向量有长度和方向决定，长度和方向不变可以随意移动，它们表示的是同一个向量。计算机中的向量更多的是对数据的抽象，可以根据面积和价格定义一个房子一列数。

通过次序中的索引，我们可以确定每个单独的数。用粗体的小写变量名称，比如

线性代数中的向量可以理解为一个空间中的箭头，这个箭头起点落在原点。如果空间中有许多的向量，可以点表示一个向量，即向量头的坐标。

向量的加法：可以理解为在坐标中两个向量的移动。对于二维向量来说，例如：

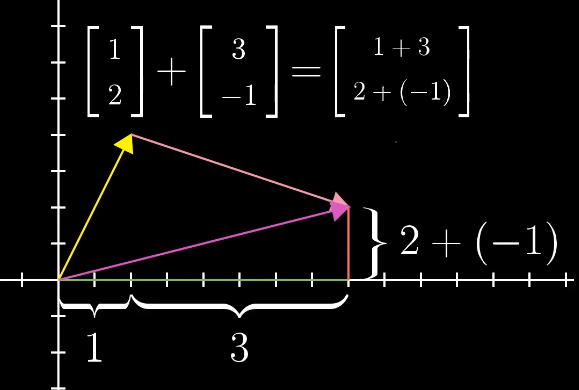
数字和向量相乘：可以理解为向量的缩放。

矩阵(matrix)：一个二维数组，其中的每一个元素被两个索引（而非一个）所确定。粗体的大写变量名称，比如

张量(tensor)：一个数组（一般超过两维的）中的元素分布在若干维坐标的规则网格中. 张量中坐标为的元素记作。

直观理解：

alt alt

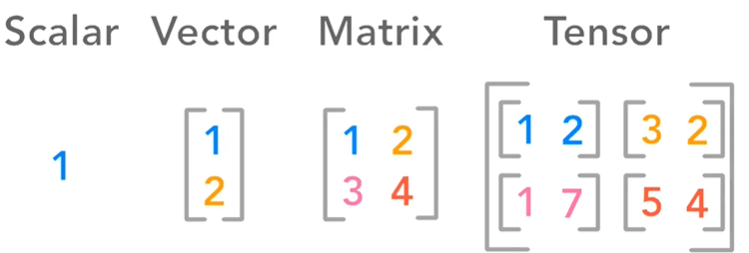
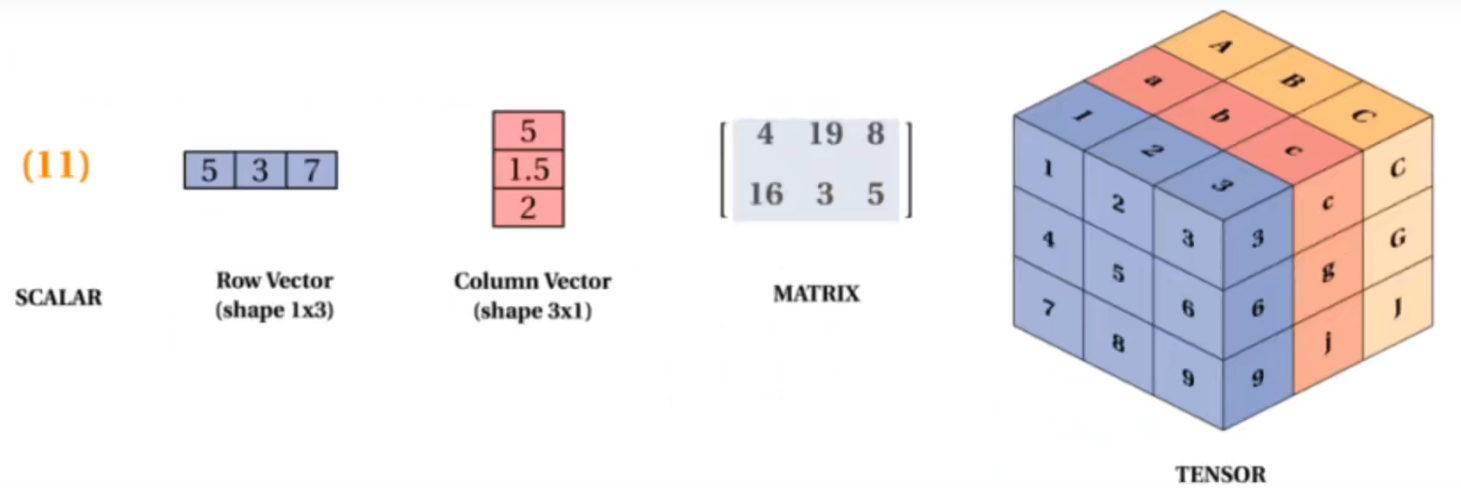
向量与矩阵的操作

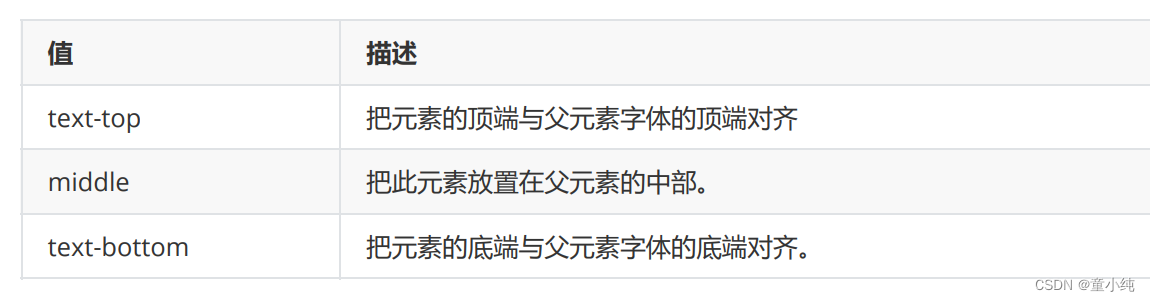
转置（transpose）：是以对角线为轴的镜像

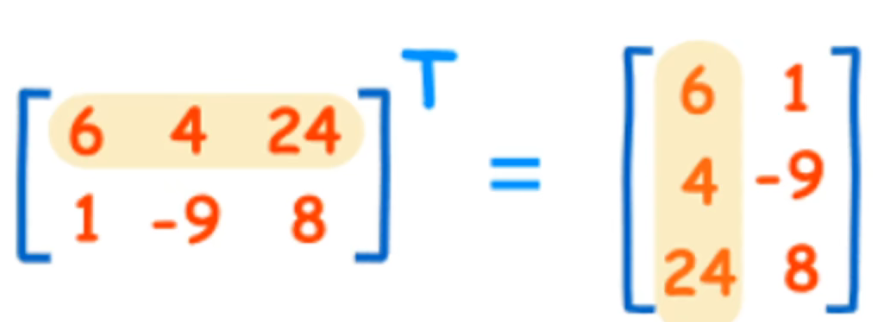
矩阵相加：只要矩阵的形状一样，我们可以把两个矩阵相加。两个矩阵相加是指对应位置的元素相加，比如，其中。

标量与矩阵相乘或相加：将其与矩阵的每个元素相乘或相加，比如，其中

广播(broadcasting):在深度学习中，我们也使用一些不那么常规的符号。允许矩阵和向量相加，产生一个新矩阵：其中，即向量和矩阵的每一行相加。

## 例
import numpy as np
M = np.arange(9).reshape(3, 3)
C = np.arange(3).reshape(3, 1)
print("M:")
print(M)
print("C:")
print(C)
print("M+C:")
print(M+C)
---------------------------------------
M:
[[0 1 2]
 [3 4 5]
 [6 7 8]]
C:
[[0]
 [1]
 [2]]
M+C:
[[ 0  1  2]
 [ 4  5  6]
 [ 8  9 10]]

矩阵乘积(matrix product)：设两个矩阵和的乘积是，为了使乘法可被定义，必须满足 . 的形状是 x .具体地，该乘法操作定义为

元素对应乘积(element-wise product)或Hadamard乘积(Hadamard product)是两个矩阵对应元素的乘积，记为

点积(dot-product)：两个相同维数的向量和可看作矩阵乘积，即对应元素相乘相加，是一个标量。

我们可以把矩阵乘积中计算的步骤看作是的第行和的第列之间的点积。 alt

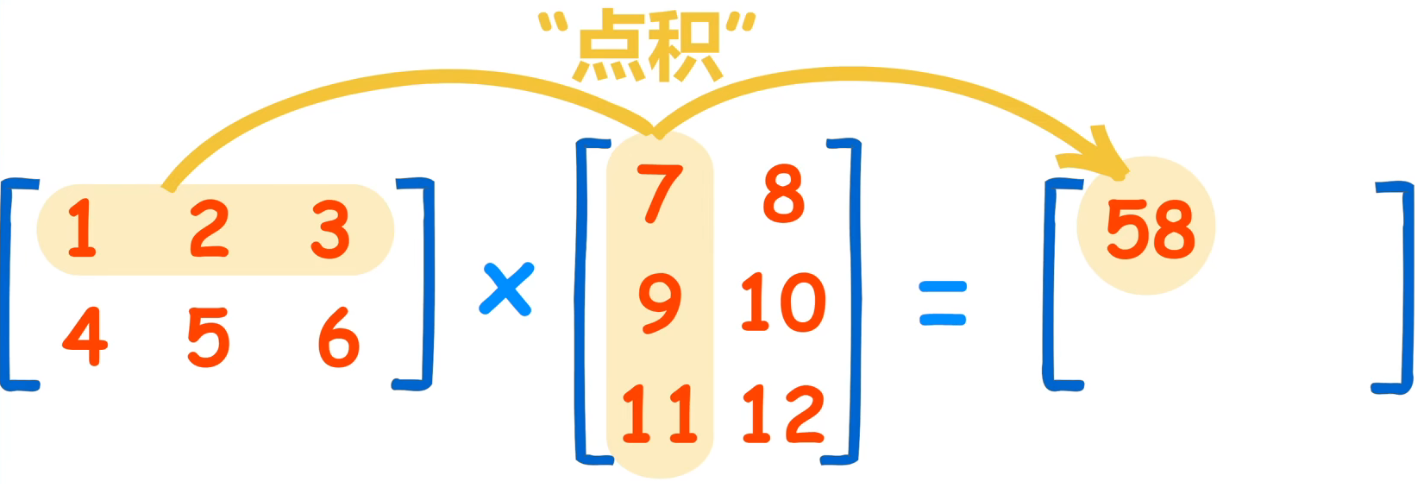
性质

(分配律)
(结合律)
(一般情况下不满足交换律)

线性方程组: 如以下线性方程组

其中和都是已知的，是要求解的未知向量。以上等式可以写为：

单位矩阵和逆矩阵

单位矩阵(identity matrix)：任意向量和单位矩阵相乘，都不会改变。我们将保持n维向量不变的单位矩阵记作（很多教材用表示单位阵），单位矩阵的所有沿主对角线的元素都是1，而其他位置的所有元素都是0.

逆矩阵:记作，其定义的矩阵满足如下条件：可以用以下步骤求解方程组：

如果逆矩阵存在，那么上式肯定对于每一个向量恰好存在一个解。逆矩阵可能也不存在

然而，逆矩阵主要是作为理论工具使用的，并不会在大多数软件应用程序中实际使用。这是因为逆矩阵在数字计算机上只能表现出有限的精度，有效使用向量的算法通常可以得到更精确的。

线性相关

在我们一般教科书上线性相关定义为：线性相关⇔至少有一个向量可以用其余向量线性表示。

❝
对二维向量而言，两个数乘向量称为两个向量的线性组合。
两个不共线的向量通过不同的线性组合可以得到二维平面中的所有向量。再看线性相关定义，这样就可以直观理解了。

❝
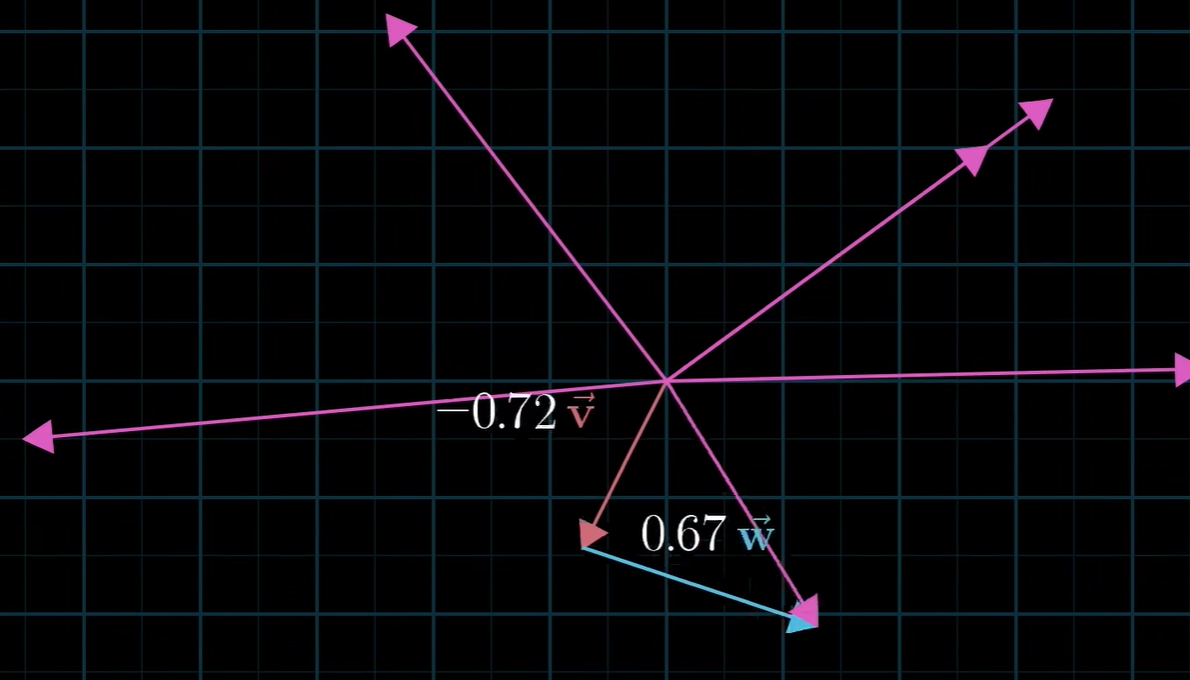
当然两个共线的向量通过线程组合只能得到一个直线的所有向量。

❝
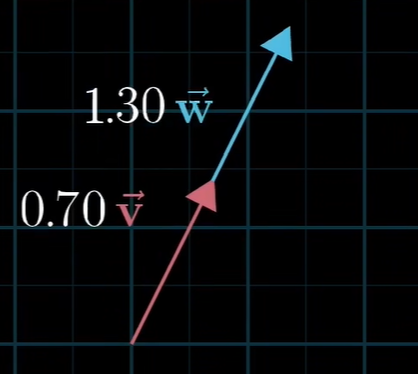
如果两个向量都是零向量那么它只能在原点。

❝
放到三维，而如果三个任意数分别乘三个不在一个平面上的三维向量则可以表示三维空间中的所有向量。
即这三个三维向量进行线性组合就可以得到这个三维空间的任意向量。
当然如果有两个向量共面,两个任意数分别乘这两个三维向量，会得到过这两个向量与原点的一个平面。即这三个向量的线性组合只能得到一个面上的所有向量。