卷积操作特征图大小计算
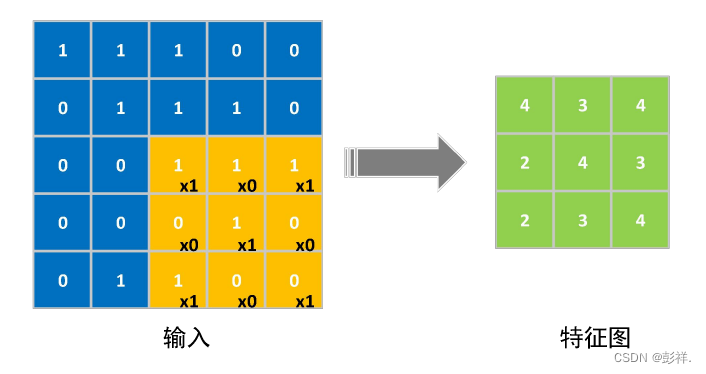
图中蓝色部分为5×5大小的输入卷积层的特征图,黄色部分 为3×3大小的卷积核,其内部黑色数字为卷积核权重参数,经过卷积操作以后得 到右侧绿色3×3大小的输出特征图。
如果使用input_N表示输入图像的大小,n表示参与卷积的卷积核尺寸,m表 示对图像扩充的大小,l表示卷积核进行一次卷积所移动的步长,则可以计算出输 出特征图的大小output_N,计算方法如式所示。
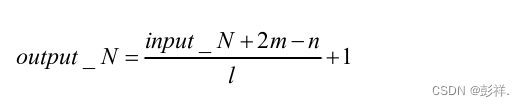
卷积操作是什么?
由以上可知,常规典型的卷积操作在对图片进行处理时采用的是线性加权运算,即卷积核矩阵与原图像矩阵作内积,而这种线性操作的拟合能力是不尽人意的,我们为使其具有良好的泛化能力,需要引 入非线性运算单元使得卷积操作具有非线性映射能力。目前的做法是在卷积操作之后把卷积结果送入非线性激活函数中。常用的激活函数有Sigmoid函数、Tanh 函数、ReLU函数等。
关于激活函数的特点
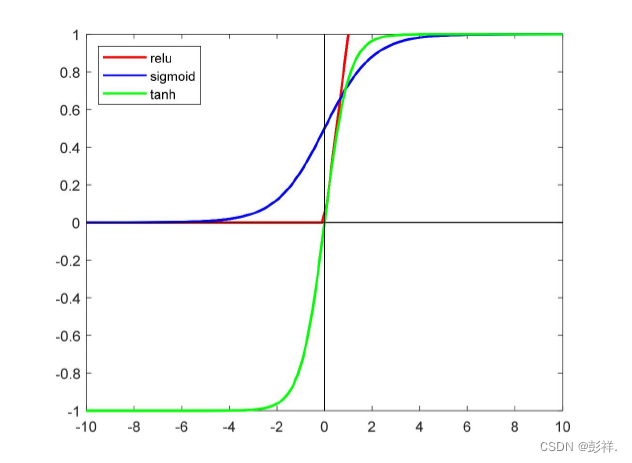
由函数曲线可知Sigmoid函数类似于指数函数,取值在0到1之间,在整个定 义域上表现为双侧有界,处处光滑可导。但是Sigmoid进行的是指数操作,在应用中计算的过程相对比较复杂。此外,这类函数还有一个很大的缺点,当输入值非常大或者非常小时,其函数曲线趋于平稳,导数值变得趋向于0,此时网络在反向传播时容易导致梯度消失的问题,使得梯度更新困难,模型的损失降低速度变慢。
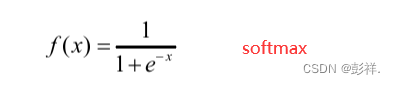
Tanh激活函数与Sigmoid十分相似,区别在于其函数图像关 于坐标轴的原点对称,值域为(-1,1)。此激活函数也为有界函数,存在饱和阶段,因此同样会有梯度消失的问题。
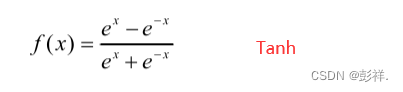
ReLU激活函数不同于以上两种指数函数,其计算方式主要为 线性运算,计算速度大大提升。此外,ReLU激活函数在激活端为无界函数,有效避免了梯度消失问题。
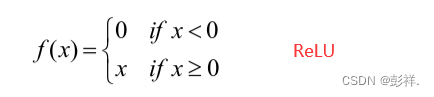
虽然ReLU激活函数对网络的梯度消失问题能有效的抑制,但是也存在导致 神经元失活的缺陷,这是由其函数性质决定的。当输入特征值小于0时,其激活 值恒等于0,同时此函数段的导数值也恒为0。这就使得该处的神经元不再对任何数据敏感,在反向传播的过程中此神经元不再更新,永久失去了活性。在实际训 练网络模型的时候,初始神经元的权重值一般设置的比较小,此时如果学习率设
置过大,则容易使得大量神经元变得无效,甚至比例可以达到40%,最后使得网络模型的损失迟迟降不下来。
针对上述梯度消失以及神经元失活的问题,人们提出了ReLU激活函数的变 体,即随机纠正线性单元RReLU。
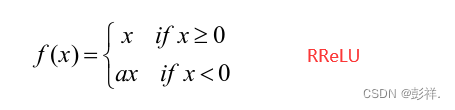
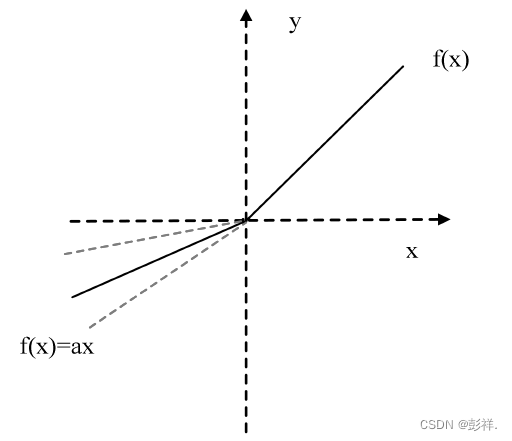
在RReLU激活函数中,当特征值小于0时函数会有一个非0的输出避免用来 避免神经元失活。负半轴函数系数a是在随机分布U(l,i)中的一个随机值,这个系数随着网络训练变化,在训练中逐渐固定下来。
高维与低维
1、靠近输入层,也就是CNN网络的浅层,一般CNN filter数量少,维度低,feature map的尺寸大,分辨率高,感受野小,所以主要包含的是局部的细节特征。
2、靠近输出层,也就是CNN网络的深层,一般CNN filter数量多,维度高,feature map的尺寸小,抽象程度高,感受野大,所以主要包含的是全局的信息。
3、我觉得这里的低维和高维,可以从feature map的channel数量也就是CNN filter数量去理解,一般我们的CNN网络都是filter数量越来越多的,而feature map经过下采样,尺寸越来越小,感受野越来越大。
池化层
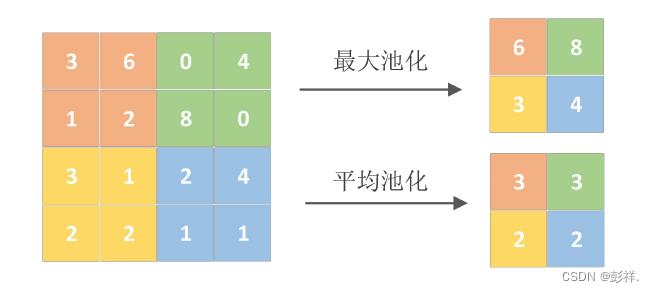
图片输入神 经网络以后因为要提取多层维度的信息,随着网络的加深特征图的通道维度变得 非常大,此时如果特征图的分辨率过大会严重增加推理速度,降低网络的实时性。 在实际场景采集的图像中,相邻像素之间往往具有很强的相关性,这就使得特征 提取时出现了信息冗余的情况。利用像素的局部相关性,在特征提取的操作中加 入池化操作获取主要特征可以解决这一问题,极大的提高计算速度。同时池化操 作可以保证图像旋转、平移以及尺度不变性。
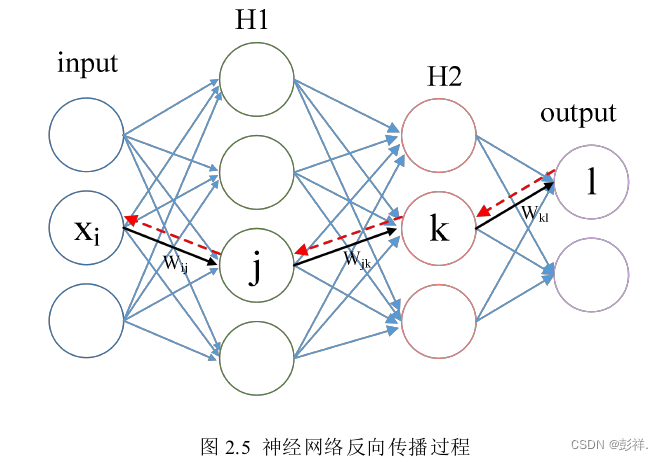
反向传播算法
深度神经网络的训练离不开反向传播算法,其实现的主要原理是使用梯度下 降算法来更新权重。主要由两个步骤组成:前向计算、反向传播。前向计算过 程中输入数据首先经过多个隐含层的处理,接着由激活函数进行非线性变换获得 最后的输出。反向传播环节中,首先对前向计算的输出数据与期望输出做对比,得到两者的输出误差即损失函数。随后根据复合函数求导得到损失函数对于各层 网络权重的梯度,以此作为网络权值修改的依据,最后更新整个网络的权值。

![[计算机毕业设计]基于SM9的密钥交换方案的实现与应用](https://img-blog.csdnimg.cn/632f16aceeee4be6a8443d20fb0be8d8.png)