目录
1.函数作用
2.函数解析
2.1 调用函数解析
2.2 Initializer::ReconstructH函数总体思路
2.2.1 代码
2.2.2 总体思路解析
3.Initializer::CheckRT
3.1 函数作用
3.2 构造函数
3.3 代码
3.4 流程解析
3.4.0 初始化参数
3.4.1 计算初始化两帧的投影矩阵
3.4.2 三角化恢复三维点Initializer::Triangulate
3.4.3 遍历所有的特征点对检查三维点是否合适
3.4.4 最后处理
1.函数作用
用H矩阵恢复R, t和三维点。
2.函数解析
2.1 调用函数解析
return ReconstructH(vbMatchesInliersH, //输入,匹配成功的特征点对Inliers标记 H, //输入,前面RANSAC计算后的单应矩阵 mK, //输入,相机的内参数矩阵 R21,t21, //输出,计算出来的相机从参考帧1到当前帧2所发生的旋转和位移变换 vP3D, //特征点对经过三角测量之后的空间坐标,也就是地图点 vbTriangulated, //特征点对是否成功三角化的标记 1.0, //这个对应的形参为minParallax,即认为某对特征点的三角化测量中,认为其测量有效时 //需要满足的最小视差角(如果视差角过小则会引起非常大的观测误差),单位是角度 50); //为了进行运动恢复,所需要的最少的三角化测量成功的点个数 该函数的调用函数为Initializer::Initialize,该函数的目的是初始化SLAM系统,即用单目初始化器的第一帧作为SLAM系统的基点并计算出第一帧和第二帧的变换矩阵并初始化地图点。此函数是在计算出H矩阵的前提下,我们想通过H矩阵来恢复单目初始化器两帧间的位姿。
输入参数为匹配成功的特征点对Inliers标记、RANSAC计算出的单应矩阵H、相机的内参、认为某对特征点的三角化测量中有效时需要满足的最小视差角、为了进行运动恢复,所需要的最少的三角化测量成功的点个数(如果恢复的3D点小于这个则认为初始化失败)
输出参数为计算出来的相机从参考帧1到当前帧2所发生的旋转和位移变换、特征点对经过三角测量之后的空间坐标,也就是地图点。
2.2 Initializer::ReconstructH函数总体思路
2.2.1 代码
/** * @brief 用H矩阵恢复R, t和三维点 * H矩阵分解常见有两种方法:Faugeras SVD-based decomposition 和 Zhang SVD-based decomposition * 代码使用了Faugeras SVD-based decomposition算法,参考文献 * Motion and structure from motion in a piecewise planar environment. International Journal of Pattern Recognition and Artificial Intelligence, 1988 * * @param[in] vbMatchesInliers 匹配点对的内点标记 * @param[in] H21 从参考帧到当前帧的单应矩阵 * @param[in] K 相机的内参数矩阵 * @param[in & out] R21 计算出来的相机旋转 * @param[in & out] t21 计算出来的相机平移 * @param[in & out] vP3D 世界坐标系下,三角化测量特征点对之后得到的特征点的空间坐标 * @param[in & out] vbTriangulated 特征点是否成功三角化的标记 * @param[in] minParallax 对特征点的三角化测量中,认为其测量有效时需要满足的最小视差角(如果视差角过小则会引起非常大的观测误差),单位是角度 * @param[in] minTriangulated 为了进行运动恢复,所需要的最少的三角化测量成功的点个数 * @return true 单应矩阵成功计算出位姿和三维点 * @return false 初始化失败 */ bool Initializer::ReconstructH(vector<bool> &vbMatchesInliers, cv::Mat &H21, cv::Mat &K, cv::Mat &R21, cv::Mat &t21, vector<cv::Point3f> &vP3D, vector<bool> &vbTriangulated, float minParallax, int minTriangulated) { // 目的 :通过单应矩阵H恢复两帧图像之间的旋转矩阵R和平移向量T // 参考 :Motion and structure from motion in a piecewise plannar environment. // International Journal of Pattern Recognition and Artificial Intelligence, 1988 // https://www.researchgate.net/publication/243764888_Motion_and_Structure_from_Motion_in_a_Piecewise_Planar_Environment // 流程: // 1. 根据H矩阵的奇异值d'= d2 或者 d' = -d2 分别计算 H 矩阵分解的 8 组解 // 1.1 讨论 d' > 0 时的 4 组解 // 1.2 讨论 d' < 0 时的 4 组解 // 2. 对 8 组解进行验证,并选择产生相机前方最多3D点的解为最优解 // 统计匹配的特征点对中属于内点(Inlier)或有效点个数 int N=0; for(size_t i=0, iend = vbMatchesInliers.size() ; i<iend; i++) if(vbMatchesInliers[i]) N++; // We recover 8 motion hypotheses using the method of Faugeras et al. // Motion and structure from motion in a piecewise planar environment. // International Journal of Pattern Recognition and Artificial Intelligence, 1988 // 参考SLAM十四讲第二版p170-p171 // H = K * (R - t * n / d) * K_inv // 其中: K表示内参数矩阵 // K_inv 表示内参数矩阵的逆 // R 和 t 表示旋转和平移向量 // n 表示平面法向量 // 令 H = K * A * K_inv // 则 A = k_inv * H * k cv::Mat invK = K.inv(); cv::Mat A = invK*H21*K; // 对矩阵A进行SVD分解 // A 等待被进行奇异值分解的矩阵 // w 奇异值矩阵 // U 奇异值分解左矩阵 // Vt 奇异值分解右矩阵,注意函数返回的是转置 // cv::SVD::FULL_UV 全部分解 // A = U * w * Vt cv::Mat U,w,Vt,V; cv::SVD::compute(A, w, U, Vt, cv::SVD::FULL_UV); // 根据文献eq(8),计算关联变量 V=Vt.t(); // 计算变量s = det(U) * det(V) // 因为det(V)==det(Vt), 所以 s = det(U) * det(Vt) float s = cv::determinant(U)*cv::determinant(Vt); // 取得矩阵的各个奇异值 float d1 = w.at<float>(0); float d2 = w.at<float>(1); float d3 = w.at<float>(2); // SVD分解正常情况下特征值di应该是正的,且满足d1>=d2>=d3 if(d1/d2<1.00001 || d2/d3<1.00001) { return false; } // 在ORBSLAM中没有对奇异值 d1 d2 d3按照论文中描述的关系进行分类讨论, 而是直接进行了计算 // 定义8中情况下的旋转矩阵、平移向量和空间向量 vector<cv::Mat> vR, vt, vn; vR.reserve(8); vt.reserve(8); vn.reserve(8); // Step 1.1 讨论 d' > 0 时的 4 组解 // 根据论文eq.(12)有 // x1 = e1 * sqrt((d1 * d1 - d2 * d2) / (d1 * d1 - d3 * d3)) // x2 = 0 // x3 = e3 * sqrt((d2 * d2 - d2 * d2) / (d1 * d1 - d3 * d3)) // 令 aux1 = sqrt((d1*d1-d2*d2)/(d1*d1-d3*d3)) // aux3 = sqrt((d2*d2-d3*d3)/(d1*d1-d3*d3)) // 则 // x1 = e1 * aux1 // x3 = e3 * aux2 // 因为 e1,e2,e3 = 1 or -1 // 所以有x1和x3有四种组合 // x1 = {aux1,aux1,-aux1,-aux1} // x3 = {aux3,-aux3,aux3,-aux3} float aux1 = sqrt((d1*d1-d2*d2)/(d1*d1-d3*d3)); float aux3 = sqrt((d2*d2-d3*d3)/(d1*d1-d3*d3)); float x1[] = {aux1,aux1,-aux1,-aux1}; float x3[] = {aux3,-aux3,aux3,-aux3}; // 根据论文eq.(13)有 // sin(theta) = e1 * e3 * sqrt(( d1 * d1 - d2 * d2) * (d2 * d2 - d3 * d3)) /(d1 + d3)/d2 // cos(theta) = (d2* d2 + d1 * d3) / (d1 + d3) / d2 // 令 aux_stheta = sqrt((d1*d1-d2*d2)*(d2*d2-d3*d3))/((d1+d3)*d2) // 则 sin(theta) = e1 * e3 * aux_stheta // cos(theta) = (d2*d2+d1*d3)/((d1+d3)*d2) // 因为 e1 e2 e3 = 1 or -1 // 所以 sin(theta) = {aux_stheta, -aux_stheta, -aux_stheta, aux_stheta} float aux_stheta = sqrt((d1*d1-d2*d2)*(d2*d2-d3*d3))/((d1+d3)*d2); float ctheta = (d2*d2+d1*d3)/((d1+d3)*d2); float stheta[] = {aux_stheta, -aux_stheta, -aux_stheta, aux_stheta}; // 计算旋转矩阵 R' //根据不同的e1 e3组合所得出来的四种R t的解 // | ctheta 0 -aux_stheta| | aux1| // Rp = | 0 1 0 | tp = | 0 | // | aux_stheta 0 ctheta | |-aux3| // | ctheta 0 aux_stheta| | aux1| // Rp = | 0 1 0 | tp = | 0 | // |-aux_stheta 0 ctheta | | aux3| // | ctheta 0 aux_stheta| |-aux1| // Rp = | 0 1 0 | tp = | 0 | // |-aux_stheta 0 ctheta | |-aux3| // | ctheta 0 -aux_stheta| |-aux1| // Rp = | 0 1 0 | tp = | 0 | // | aux_stheta 0 ctheta | | aux3| // 开始遍历这四种情况中的每一种 for(int i=0; i<4; i++) { //生成Rp,就是eq.(8) 的 R' cv::Mat Rp=cv::Mat::eye(3,3,CV_32F); Rp.at<float>(0,0)=ctheta; Rp.at<float>(0,2)=-stheta[i]; Rp.at<float>(2,0)=stheta[i]; Rp.at<float>(2,2)=ctheta; // eq.(8) 计算R cv::Mat R = s*U*Rp*Vt; // 保存 vR.push_back(R); // eq. (14) 生成tp cv::Mat tp(3,1,CV_32F); tp.at<float>(0)=x1[i]; tp.at<float>(1)=0; tp.at<float>(2)=-x3[i]; tp*=d1-d3; // 这里虽然对t有归一化,并没有决定单目整个SLAM过程的尺度 // 因为CreateInitialMapMonocular函数对3D点深度会缩放,然后反过来对 t 有改变 // eq.(8)恢复原始的t cv::Mat t = U*tp; vt.push_back(t/cv::norm(t)); // 构造法向量np cv::Mat np(3,1,CV_32F); np.at<float>(0)=x1[i]; np.at<float>(1)=0; np.at<float>(2)=x3[i]; // eq.(8) 恢复原始的法向量 cv::Mat n = V*np; //看PPT 16页的图,保持平面法向量向上 if(n.at<float>(2)<0) n=-n; // 添加到vector vn.push_back(n); } // Step 1.2 讨论 d' < 0 时的 4 组解 float aux_sphi = sqrt((d1*d1-d2*d2)*(d2*d2-d3*d3))/((d1-d3)*d2); // cos_theta项 float cphi = (d1*d3-d2*d2)/((d1-d3)*d2); // 考虑到e1,e2的取值,这里的sin_theta有两种可能的解 float sphi[] = {aux_sphi, -aux_sphi, -aux_sphi, aux_sphi}; // 对于每种由e1 e3取值的组合而形成的四种解的情况 for(int i=0; i<4; i++) { // 计算旋转矩阵 R' cv::Mat Rp=cv::Mat::eye(3,3,CV_32F); Rp.at<float>(0,0)=cphi; Rp.at<float>(0,2)=sphi[i]; Rp.at<float>(1,1)=-1; Rp.at<float>(2,0)=sphi[i]; Rp.at<float>(2,2)=-cphi; // 恢复出原来的R cv::Mat R = s*U*Rp*Vt; // 然后添加到vector中 vR.push_back(R); // 构造tp cv::Mat tp(3,1,CV_32F); tp.at<float>(0)=x1[i]; tp.at<float>(1)=0; tp.at<float>(2)=x3[i]; tp*=d1+d3; // 恢复出原来的t cv::Mat t = U*tp; // 归一化之后加入到vector中,要提供给上面的平移矩阵都是要进行过归一化的 vt.push_back(t/cv::norm(t)); // 构造法向量np cv::Mat np(3,1,CV_32F); np.at<float>(0)=x1[i]; np.at<float>(1)=0; np.at<float>(2)=x3[i]; // 恢复出原来的法向量 cv::Mat n = V*np; // 保证法向量指向上方 if(n.at<float>(2)<0) n=-n; // 添加到vector中 vn.push_back(n); } // 最好的good点 int bestGood = 0; // 其次最好的good点 int secondBestGood = 0; // 最好的解的索引,初始值为-1 int bestSolutionIdx = -1; // 最大的视差角 float bestParallax = -1; // 存储最好解对应的,对特征点对进行三角化测量的结果 vector<cv::Point3f> bestP3D; // 最佳解所对应的,那些可以被三角化测量的点的标记 vector<bool> bestTriangulated; // Instead of applying the visibility constraints proposed in the WFaugeras' paper (which could fail for points seen with low parallax) // We reconstruct all hypotheses and check in terms of triangulated points and parallax // Step 2. 对 8 组解进行验证,并选择产生相机前方最多3D点的解为最优解 for(size_t i=0; i<8; i++) { // 第i组解对应的比较大的视差角 float parallaxi; // 三角化测量之后的特征点的空间坐标 vector<cv::Point3f> vP3Di; // 特征点对是否被三角化的标记 vector<bool> vbTriangulatedi; // 调用 Initializer::CheckRT(), 计算good点的数目 int nGood = CheckRT(vR[i],vt[i], //当前组解的旋转矩阵和平移向量 mvKeys1,mvKeys2, //特征点 mvMatches12,vbMatchesInliers, //特征匹配关系以及Inlier标记 K, //相机的内参数矩阵 vP3Di, //存储三角化测量之后的特征点空间坐标的 4.0*mSigma2, //三角化过程中允许的最大重投影误差 vbTriangulatedi, //特征点是否被成功进行三角测量的标记 parallaxi); // 这组解在三角化测量的时候的比较大的视差角 // 更新历史最优和次优的解 // 保留最优的和次优的解.保存次优解的目的是看看最优解是否突出 if(nGood>bestGood) { // 如果当前组解的good点数是历史最优,那么之前的历史最优就变成了历史次优 secondBestGood = bestGood; // 更新历史最优点 bestGood = nGood; // 最优解的组索引为i(就是当前次遍历) bestSolutionIdx = i; // 更新变量 bestParallax = parallaxi; bestP3D = vP3Di; bestTriangulated = vbTriangulatedi; } // 如果当前组的good计数小于历史最优但却大于历史次优 else if(nGood>secondBestGood) { // 说明当前组解是历史次优点,更新之 secondBestGood = nGood; } } // Step 3 选择最优解。要满足下面的四个条件 // 1. good点数最优解明显大于次优解,这里取0.75经验值 // 2. 视角差大于规定的阈值 // 3. good点数要大于规定的最小的被三角化的点数量 // 4. good数要足够多,达到总数的90%以上 if(secondBestGood<0.75*bestGood && bestParallax>=minParallax && bestGood>minTriangulated && bestGood>0.9*N) { // 从最佳的解的索引访问到R,t vR[bestSolutionIdx].copyTo(R21); vt[bestSolutionIdx].copyTo(t21); // 获得最佳解时,成功三角化的三维点,以后作为初始地图点使用 vP3D = bestP3D; // 获取特征点的被成功进行三角化的标记 vbTriangulated = bestTriangulated; //返回真,找到了最好的解 return true; } return false; }
2.2.2 总体思路解析
1. 根据H矩阵的奇异值d'= d2 或者 d' = -d2 分别计算 H 矩阵分解的 8 组解(不需要明白)
1.1 讨论 d' > 0 时的 4 组解
1.2 讨论 d' < 0 时的 4 组解
2. 对 8 组解进行验证,并选择产生相机前方最多3D点的解为最优解。(CheckRT)这里分解为八组解为论文中所做的事情,我们不加解释,主要将这八组解解出的R,t,这8 组解进行验证,并选择产生相机前方最多3D点的解为最优解。
总体思路:我们按照论文所作计算出了八组
解,对每一个解进行验证(计算能恢复的3D点数量),记录恢复3D点最多和次多的
解。判断:
如果:
①0.75倍最优解的数量大于次优解(保证系统鲁棒性)
②视角差大于规定的阈值
③good点数要大于规定的最小的被三角化的点数量
④good数要足够多,达到总数的90%以上则:
选取这组解的
作为地图初始化的
,这组解初始化的3D点作为初始地图点使用,获取特征点的被成功进行三角化的标记,向上层函数返回true表示单目初始化成功。
3.Initializer::CheckRT
3.1 函数作用
用位姿来对特征匹配点三角化,从中筛选中合格的三维点。
3.2 构造函数
* @brief 用位姿来对特征匹配点三角化,从中筛选中合格的三维点 * * @param[in] R 旋转矩阵R * @param[in] t 平移矩阵t * @param[in] vKeys1 参考帧特征点 * @param[in] vKeys2 当前帧特征点 * @param[in] vMatches12 两帧特征点的匹配关系 * @param[in] vbMatchesInliers 特征点对内点标记 * @param[in] K 相机内参矩阵 * @param[in & out] vP3D 三角化测量之后的特征点的空间坐标 * @param[in] th2 重投影误差的阈值 * @param[in & out] vbGood 标记成功三角化点? * @param[in & out] parallax 计算出来的比较大的视差角(注意不是最大,具体看后面代码) * @return int */ int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2, const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers, const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float ¶llax)传入参数:
①参考帧到当前帧的旋转矩阵R和平移矩阵t
②参考帧(第一帧)和当前帧(第二帧)的特征点容器vKeys1、vKeys2
③两帧特征点的匹配标记vMatches12以及特征点对内点标记vbMatchesInliers
④相机内参K,重投影误差阈值th2
传出参数:
①三角化测量之后的特征点的空间坐标v3D
②标记成功三角化点vGoog
③返回三角化点的数量
3.3 代码
int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2, const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers, const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float ¶llax) { // 对给出的特征点对及其R t , 通过三角化检查解的有效性,也称为 cheirality check // Calibration parameters //从相机内参数矩阵获取相机的校正参数 const float fx = K.at<float>(0,0); const float fy = K.at<float>(1,1); const float cx = K.at<float>(0,2); const float cy = K.at<float>(1,2); //特征点是否是good点的标记,这里的特征点指的是参考帧中的特征点 vbGood = vector<bool>(vKeys1.size(),false); //重设存储空间坐标的点的大小 vP3D.resize(vKeys1.size()); //存储计算出来的每对特征点的视差 vector<float> vCosParallax; vCosParallax.reserve(vKeys1.size()); // Camera 1 Projection Matrix K[I|0] // Step 1:计算相机的投影矩阵 // 投影矩阵P是一个 3x4 的矩阵,可以将空间中的一个点投影到平面上,获得其平面坐标,这里均指的是齐次坐标。 // 对于第一个相机是 P1=K*[I|0] // 以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵 cv::Mat P1(3,4, //矩阵的大小是3x4 CV_32F, //数据类型是浮点数 cv::Scalar(0)); //初始的数值是0 //将整个K矩阵拷贝到P1矩阵的左侧3x3矩阵,因为 K*I = K K.copyTo(P1.rowRange(0,3).colRange(0,3)); // 第一个相机的光心设置为世界坐标系下的原点 cv::Mat O1 = cv::Mat::zeros(3,1,CV_32F); // Camera 2 Projection Matrix K[R|t] // 计算第二个相机的投影矩阵 P2=K*[R|t] cv::Mat P2(3,4,CV_32F); R.copyTo(P2.rowRange(0,3).colRange(0,3)); t.copyTo(P2.rowRange(0,3).col(3)); //最终结果是K*[R|t] P2 = K*P2; // 第二个相机的光心在世界坐标系下的坐标 cv::Mat O2 = -R.t()*t; //在遍历开始前,先将good点计数设置为0 int nGood=0; // 开始遍历所有的特征点对 for(size_t i=0, iend=vMatches12.size();i<iend;i++) { // 跳过outliers if(!vbMatchesInliers[i]) continue; // Step 2 获取特征点对,调用Triangulate() 函数进行三角化,得到三角化测量之后的3D点坐标 // kp1和kp2是匹配好的有效特征点 const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first]; const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second]; //存储三维点的的坐标 cv::Mat p3dC1; // 利用三角法恢复三维点p3dC1 Triangulate(kp1,kp2, //特征点 P1,P2, //投影矩阵 p3dC1); //输出,三角化测量之后特征点的空间坐标 // Step 3 第一关:检查三角化的三维点坐标是否合法(非无穷值) // 只要三角测量的结果中有一个是无穷大的就说明三角化失败,跳过对当前点的处理,进行下一对特征点的遍历 if(!isfinite(p3dC1.at<float>(0)) || !isfinite(p3dC1.at<float>(1)) || !isfinite(p3dC1.at<float>(2))) { //其实这里就算是不这样写也没问题,因为默认的匹配点对就不是good点 vbGood[vMatches12[i].first]=false; //继续对下一对匹配点的处理 continue; } // Check parallax // Step 4 第二关:通过三维点深度值正负、两相机光心视差角大小来检查是否合法 //得到向量PO1 cv::Mat normal1 = p3dC1 - O1; //求取模长,其实就是距离 float dist1 = cv::norm(normal1); //同理构造向量PO2 cv::Mat normal2 = p3dC1 - O2; //求模长 float dist2 = cv::norm(normal2); //根据公式:a.*b=|a||b|cos_theta 可以推导出来下面的式子 float cosParallax = normal1.dot(normal2)/(dist1*dist2); // Check depth in front of first camera (only if enough parallax, as "infinite" points can easily go to negative depth) // 如果深度值为负值,为非法三维点跳过该匹配点对 // ?视差比较小时,重投影误差比较大。这里0.99998 对应的角度为0.36°,这里不应该是 cosParallax>0.99998 吗? // ?因为后面判断vbGood 点时的条件也是 cosParallax<0.99998 // !可能导致初始化不稳定 if(p3dC1.at<float>(2)<=0 && cosParallax<0.99998) continue; // Check depth in front of second camera (only if enough parallax, as "infinite" points can easily go to negative depth) // 讲空间点p3dC1变换到第2个相机坐标系下变为p3dC2 cv::Mat p3dC2 = R*p3dC1+t; //判断过程和上面的相同 if(p3dC2.at<float>(2)<=0 && cosParallax<0.99998) continue; // Step 5 第三关:计算空间点在参考帧和当前帧上的重投影误差,如果大于阈值则舍弃 // Check reprojection error in first image // 计算3D点在第一个图像上的投影误差 //投影到参考帧图像上的点的坐标x,y float im1x, im1y; //这个使能空间点的z坐标的倒数 float invZ1 = 1.0/p3dC1.at<float>(2); //投影到参考帧图像上。因为参考帧下的相机坐标系和世界坐标系重合,因此这里就直接进行投影就可以了 im1x = fx*p3dC1.at<float>(0)*invZ1+cx; im1y = fy*p3dC1.at<float>(1)*invZ1+cy; //参考帧上的重投影误差,这个的确就是按照定义来的 float squareError1 = (im1x-kp1.pt.x)*(im1x-kp1.pt.x)+(im1y-kp1.pt.y)*(im1y-kp1.pt.y); // 重投影误差太大,跳过淘汰 if(squareError1>th2) continue; // Check reprojection error in second image // 计算3D点在第二个图像上的投影误差,计算过程和第一个图像类似 float im2x, im2y; // 注意这里的p3dC2已经是第二个相机坐标系下的三维点了 float invZ2 = 1.0/p3dC2.at<float>(2); im2x = fx*p3dC2.at<float>(0)*invZ2+cx; im2y = fy*p3dC2.at<float>(1)*invZ2+cy; // 计算重投影误差 float squareError2 = (im2x-kp2.pt.x)*(im2x-kp2.pt.x)+(im2y-kp2.pt.y)*(im2y-kp2.pt.y); // 重投影误差太大,跳过淘汰 if(squareError2>th2) continue; // Step 6 统计经过检验的3D点个数,记录3D点视差角 // 如果运行到这里就说明当前遍历的这个特征点对靠谱,经过了重重检验,说明是一个合格的点,称之为good点 vCosParallax.push_back(cosParallax); //存储这个三角化测量后的3D点在世界坐标系下的坐标 vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0),p3dC1.at<float>(1),p3dC1.at<float>(2)); //good点计数++ nGood++; //判断视差角,只有视差角稍稍大一丢丢的才会给打good点标记 //? bug 我觉得这个写的位置不太对。你的good点计数都++了然后才判断,不是会让good点标志和good点计数不一样吗 if(cosParallax<0.99998) vbGood[vMatches12[i].first]=true; } // Step 7 得到3D点中较小的视差角,并且转换成为角度制表示 if(nGood>0) { // 从小到大排序,注意vCosParallax值越大,视差越小 sort(vCosParallax.begin(),vCosParallax.end()); // !排序后并没有取最小的视差角,而是取一个较小的视差角 // 作者的做法:如果经过检验过后的有效3D点小于50个,那么就取最后那个最小的视差角(cos值最大) // 如果大于50个,就取排名第50个的较小的视差角即可,为了避免3D点太多时出现太小的视差角 size_t idx = min(50,int(vCosParallax.size()-1)); //将这个选中的角弧度制转换为角度制 parallax = acos(vCosParallax[idx])*180/CV_PI; } else //如果没有good点那么这个就直接设置为0了 parallax=0; //返回good点计数 return nGood; }
3.4 流程解析
3.4.0 初始化参数
①特征点是否是good点的标记,这里的特征点指的是参考帧中的特征点,将vGood初始化为第一帧特征点的数量,其为bool类型。
②三角化测量之后的特征点的空间坐标v3D初始化大小为第一帧中特征点的数量。
3.4.1 计算初始化两帧的投影矩阵
投影矩阵P是一个 3x4 的矩阵,可以将空间中的一个点投影到平面上,获得其平面坐标,这里均指的是齐次坐标。
由于以第一个相机的光心作为世界坐标系。 其投影矩阵计算推导如下:
我们默认第一个相机的
矩阵为
,因此第一个相机的投影矩阵为
。第一个相机的光心坐标为
。
我们从传入参数可知第一个相机到第二个相机的
变换
,因此再左乘相机内参矩阵
就能得到像素坐标,即世界坐标向像素坐标的投影矩阵为
。
同时计算第二帧的光心坐标在原点(第一帧)的坐标,计算如下图所示:
第二个相机的光心在世界坐标系下的坐标,即我们要求第二个相机的光心在第一个相机坐标系下的坐标。
3.4.2 三角化恢复三维点Initializer::Triangulate
1.数学原理
我们将投影方程进行如下描述:
为方便推导,简单记为:
为了化为齐次方程,左右两边同时叉乘,得到:
利用两对匹配点,得到:
SVD求解,右奇异矩阵的最后一行就是最终的解。
2.代码
/** 给定投影矩阵P1,P2和图像上的匹配特征点点kp1,kp2,从而计算三维点坐标 * @brief * * @param[in] kp1 特征点, in reference frame * @param[in] kp2 特征点, in current frame * @param[in] P1 投影矩阵P1 * @param[in] P2 投影矩阵P2 * @param[in & out] x3D 计算的三维点 */ void Initializer::Triangulate( const cv::KeyPoint &kp1, //特征点, in reference frame const cv::KeyPoint &kp2, //特征点, in current frame const cv::Mat &P1, //投影矩阵P1 const cv::Mat &P2, //投影矩阵P2 cv::Mat &x3D) //三维点 { // 原理 // Trianularization: 已知匹配特征点对{x x'} 和 各自相机矩阵{P P'}, 估计三维点 X // x' = P'X x = PX // 它们都属于 x = aPX模型 // |X| // |x| |p1 p2 p3 p4 ||Y| |x| |--p0--||.| // |y| = a |p5 p6 p7 p8 ||Z| ===>|y| = a|--p1--||X| // |z| |p9 p10 p11 p12||1| |z| |--p2--||.| // 采用DLT的方法:x叉乘PX = 0 // |yp2 - p1| |0| // |p0 - xp2| X = |0| // |xp1 - yp0| |0| // 两个点: // |yp2 - p1 | |0| // |p0 - xp2 | X = |0| ===> AX = 0 // |y'p2' - p1' | |0| // |p0' - x'p2'| |0| // 变成程序中的形式: // |xp2 - p0 | |0| // |yp2 - p1 | X = |0| ===> AX = 0 // |x'p2'- p0'| |0| // |y'p2'- p1'| |0| // 然后就组成了一个四元一次正定方程组,SVD求解,右奇异矩阵的最后一行就是最终的解. //这个就是上面注释中的矩阵A cv::Mat A(4,4,CV_32F); //构造参数矩阵A A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0); A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1); A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0); A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1); //奇异值分解的结果 cv::Mat u,w,vt; //对系数矩阵A进行奇异值分解 cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV); //根据前面的结论,奇异值分解右矩阵的最后一行其实就是解,原理类似于前面的求最小二乘解,四个未知数四个方程正好正定 //别忘了我们更习惯用列向量来表示一个点的空间坐标 x3D = vt.row(3).t(); //为了符合其次坐标的形式,使最后一维为1 x3D = x3D.rowRange(0,3)/x3D.at<float>(3); }至此我们恢复一对匹配特征点的3D点。
3.4.3 遍历所有的特征点对检查三维点是否合适
我们遍历所有匹配的特征点对,如果不是外点,则将匹配好的特征点对传入Initializer::Triangulate函数内得到三维点。我们对三维点进行判断:
①检查三角化的三维点坐标是否合法:防止三角化出的点有一维坐标是无穷。
②通过三维点深度值正负、两相机光心视差角大小来检查是否合法 。即判断如果深度值为负值,为非法三维点跳过该匹配点对。计算视差角,当视差角比较小时,重投影误差比较大。
③计算空间点在参考帧和当前帧上的重投影误差,如果大于阈值则舍弃。计算3D点在第一、二个图像上的投影误差,看是否超过阈值选择是否抛弃。
如果如上满足了,这个3D点可以被留下来,用vCosParallax向量存储合格3D点生成时计算出来的视差,存储这个三角化测量后的3D点在世界坐标系下的坐标。并将这两帧累计成功初始化的3D点nGood累加。
vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0),p3dC1.at<float>(1),p3dC1.at<float>(2));
3.4.4 最后处理
如果我们的变量nGood大于0(成功三角化得到的3D点的数目),我们将视差角从小到大排序,排序后并没有取最小的视差角,而是取一个较小的视差角。如果经过检验过后的有效3D点小于50个,那么就取最后那个最小的视差角(cos值最大),如果大于50个,就取排名第50个的较小的视差角即可,为了避免3D点太多时出现太小的视差角。将这个选中的角弧度制转换为角度制输出。
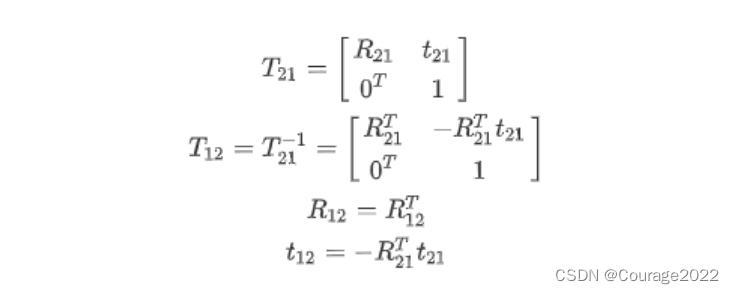
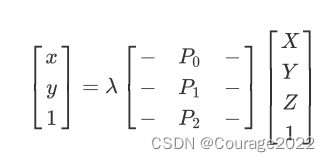

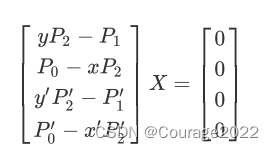
![[计算机毕业设计]基于SM9的密钥交换方案的实现与应用](https://img-blog.csdnimg.cn/632f16aceeee4be6a8443d20fb0be8d8.png)