**🛀 ♡ ♢ ♤ ♧ ♣ ♦ ♥ ♠🛀**
💥**欢迎来到半之半的博客**,**这篇文章主要讲述数据结构中非常重要的一块内容,
即树与二叉树,相信大家学完必会加深自己的理解。💥**
**🕝我是半只半,一个大二的在校学生🕥**
**🕟喜欢的朋友可以关注一下,下次更新不迷路hh🕤**
💌前言
🧡学习目标
- 掌握二叉树的定义、性质、存储结构
- 掌握二叉树的先序、中序和后序遍历方法
- 掌握二叉树线索化方法
- 掌握哈夫曼树的建立和哈夫曼编码方法
- 掌握树和森林和二叉树的相互转换
🧡学习重点
- 二叉树的性质、遍历
- 哈夫曼树及哈夫曼编码
🧡学习难点
- 二叉树的线索化、
- 哈夫曼树及哈夫曼编码
🤦♂️二叉树的存储结构
🧟♀️二叉树的顺序结构
实现一般是按满(完全)二叉树的结点编号,依次存放二叉树中的数据元素。
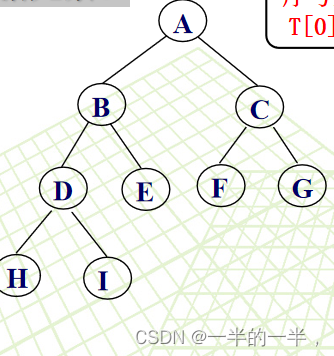
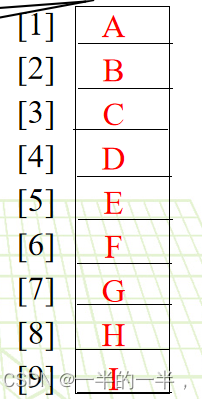
如果不是完全二叉树呢?
先转化为完全二叉树。
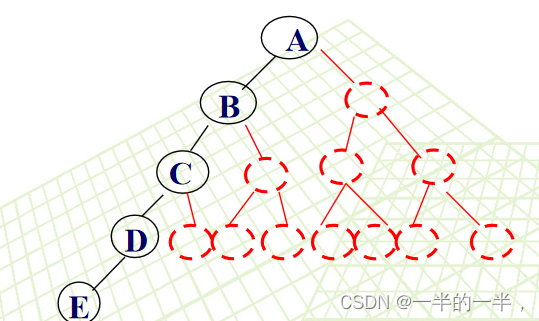
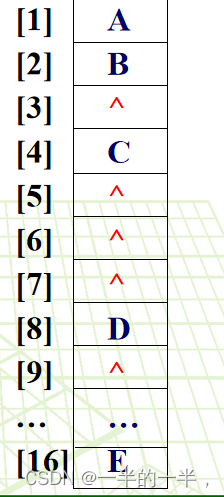
缺点:浪费空间
二叉树的链式结构
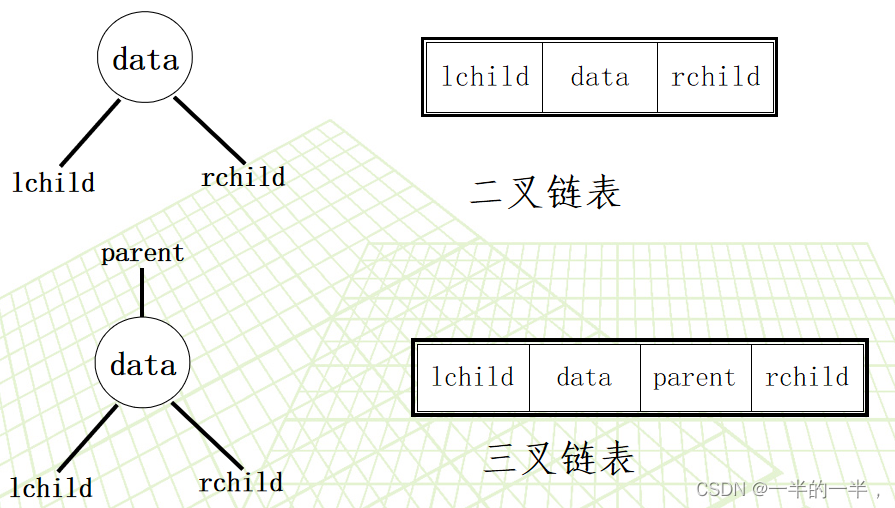
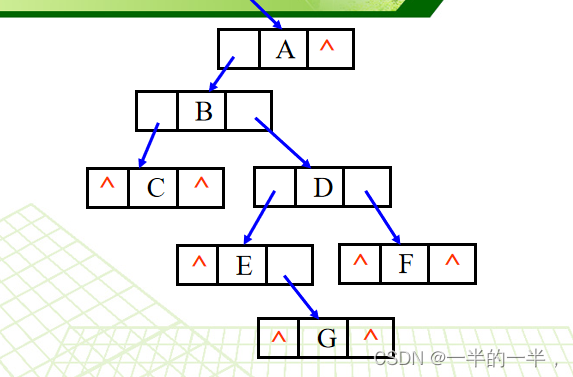
二叉链表结点类定义:
class BiNode<T>{
T data;
BiNode<T> lchild,rchild; //左右孩子指针
public BiNode(T data,BiNode left,BiNode right){
this.data = data; this.lchild = left;
this.rchild = right; }
public BiNode(T data){ this(data ,null,null);}
public String toString(){return this.data.toString();}
public boolean isLeaf(){
return lchild==null && rchild==null; }
二叉树类定义:
public class BiTree<T>{
BiNode<T> root;
public BiTree(){
this.root = null; //初始化空二叉树
}
public boolean isEmpty(){
return this.root==null;
}
…… //其他操作
}
在n个结点的二叉链表中,有 n+1 个空指针域。
分析:
n个结点必有2n个链域。
除根结点外,每个结点有且仅有一个双亲,所以只会有n-1个结点的链域存放指针,指向非空子女结点。
🐱🚀二叉树的遍历
遍历定义——指按某条搜索路线遍访每个结点且不重复(又称周游)。
遍历用途——它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
遍历实质——将非线性结构线性化。
先序遍历
若二叉树为空,则空操作;
否则:(1)访问根结点 (D)(2)先序遍历左子树 (L)(3)先序遍历右子树 ®
public void DLR(BiNode<T> p){
if(p!=null){
System.out.print(p.data);
DLR(p.lchild);
DLR(p.rchild);
}
}
如下图ABCD的树
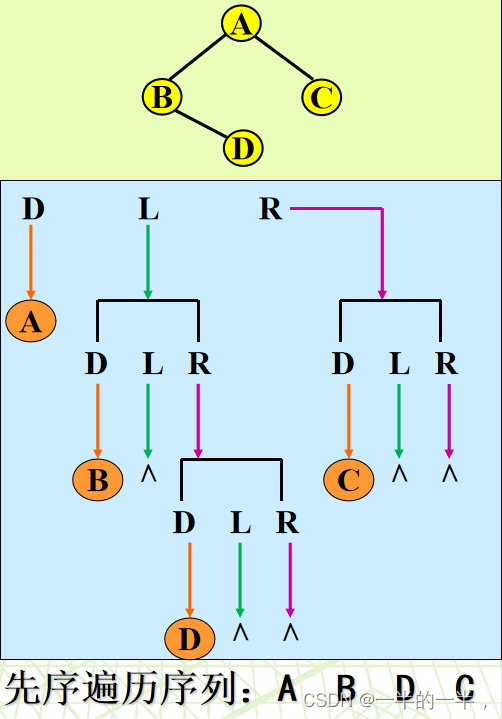
中序遍历
若二叉树为空,则空操作;
否则:(1)中序遍历左子树 (L)(2)访问根结点 (D)(3)中序遍历右子树 ®
public void LDR(BiNode<T> p){
if(p !=null){
LDR(p.lchild);
System.out.print(p.data);
LDR(p.rchild);
}
}
后序遍历
若二叉树为空,则空操作;
否则:(1)后序遍历左子树 (L)(2)后序遍历右子树 ®(3)访问根结点 (D)
public void LRD (BiNode<T> p){
if(p !=null){
LRD (p.lchild);
LRD (p.rchild);
System.out.print(p.data);
}
}
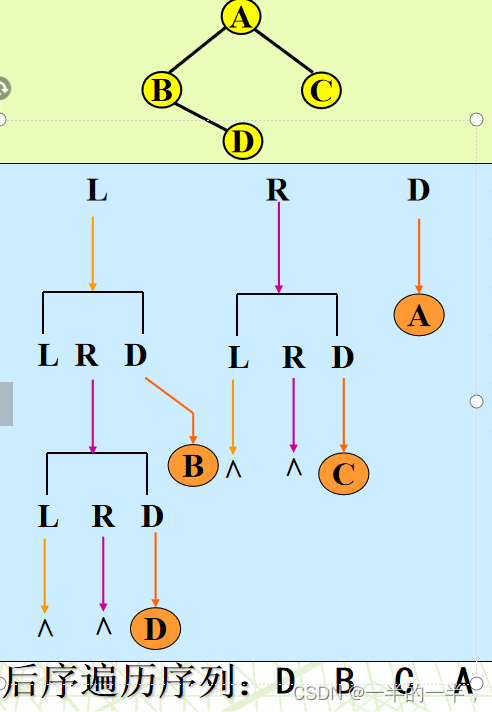
性质1
若二叉树中各结点的值均不相同,则:
由二叉树的前序序列和中序序列,或由其后序序列和中序序列均能唯一地确定一棵二叉树。(方法:先序、后序确定根,中序分左右)
但由前序序列和后序序列却不一定能唯一地确定一棵二叉树。
如已知一棵二叉树的中序序列和后序序列分别是BDCEAFHG 和 DECBHGFA,我们就可以画出这棵树,
分析:
①由后序遍历特征,根结点必在后序序列尾部(A);
②由中序遍历特征,根结点必在其中间,而且其左部必全部是左子树子孙(BDCE),其右部必全部是右子树子孙(FHG);
③继而,根据后序中的DECB子树可确定B为A的左孩子,根据HGF子串可确定F为A的右孩子;以此类推。
建立二叉树
根据先序遍历生成树的算法:
private int i = 0;
public BiNode<T> create(T[] prelist) //根据先序序列建二叉树
{ BiNode<T> p=null;
if(i<prelist.length) {
T elem = prelist[i] ; i++;
if( elem != null ) {
p = new BiTNode( elem); //生成根结点
p.lchild = create (prelist); //递归创建左子树
p.rchild = create (prelist); //递归创建右子树
}
return p;
}
同时我们还要生成数组,
public BiTree(T[] prelist)
{
this.root = create(prelist);
}
二叉树遍历的应用
计算二叉树的结点总数
如果是空树结点为0,否则,结点个数为左子树的结点个数+右子树的结点个数+1。
public int NodeCount(BiNode<T> p){
if(p== null ) return 0;
else return NodeCount(p.lchild) +
NodeCount(p.rchild)+1;
}
计算二叉树的叶子总数
如果是空树,则叶子结点个数为0;
如果只有根结点,则叶子结点个数为1;
否则,为左子树的叶子结点个数+右子树的叶子结点个数。
public int LeafCount(BiNode<T> p){
if(p== null) return 0; //如果是空树返回0
if (p.lchild==null && p.rchild==null)
return 1; //如果是叶子结点返回1
else return LeafCount(p.lchild) + LeafCount(p.rchild);
}
线索二叉树
- 二叉树存储了其左右孩子信息,而该结点在遍历序列中的直接前驱和直接后继只能在遍历过程中获得。
- 得到二叉树一个结点在某个遍历序列里的直接前驱和直接后继信息: 再进行一次遍历(费时)
- 结点中增加两条链,分别指向某遍历序列中的前驱、后继。(费空间)
若结点有左子树,则lchild指向其左孩子;否则, lchild指向遍历序列中其直接前驱(即线索);若结点有右子树,则rchild指向其右孩子;否则, rchild指向遍历序列中其直接后继(即线索) 。
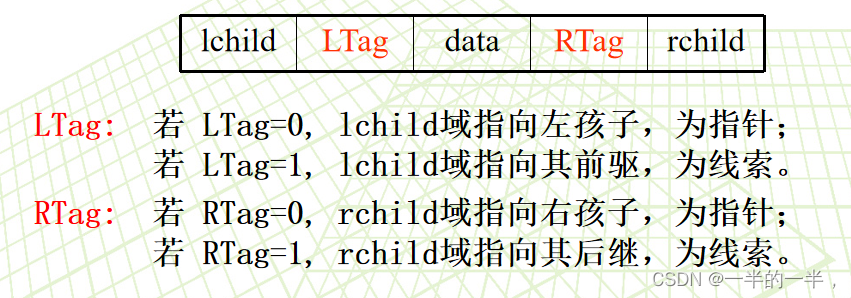
我们可以举个例子
先序线索二叉树
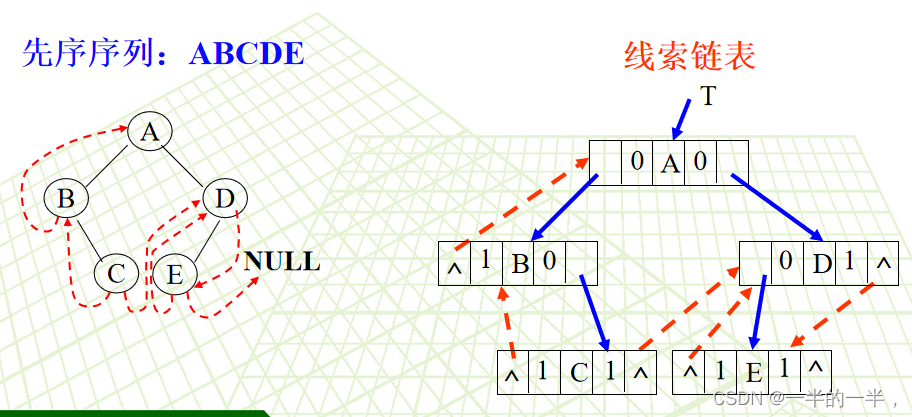
中序线索二叉树
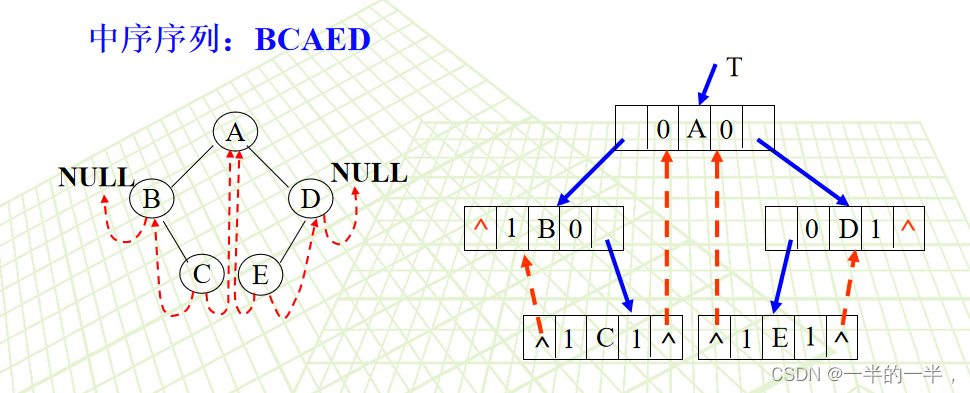
后序线索二叉树
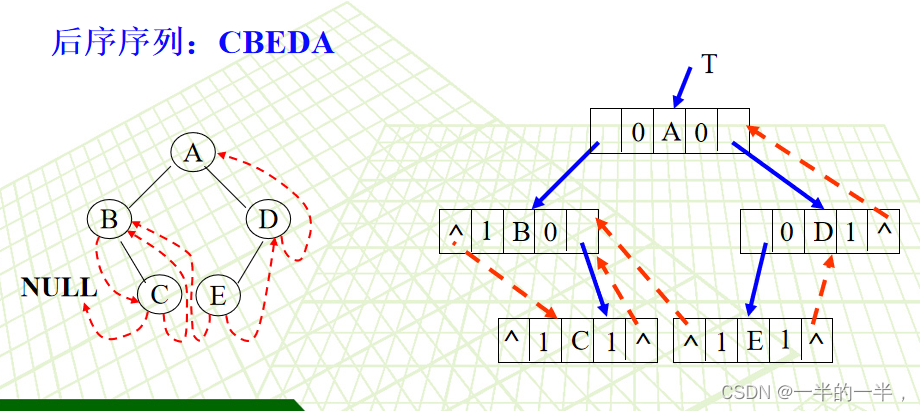
🐱🚀后记
- 🕟本章才刚刚开始哦
- 🕟谢谢您的访问
- 🕟觉得博主写的好来个三连

![[计算机毕业设计]基于SM9的密钥交换方案的实现与应用](https://img-blog.csdnimg.cn/632f16aceeee4be6a8443d20fb0be8d8.png)