数据标准化处理代码解析

在数据分析和机器学习领域，数据标准化是一个重要的预处理步骤，它可以使不同特征的数据具有可比性，提高模型的性能。本文将详细解析一段Python代码，该代码实现了对用户每月支出数据的三种标准化方法：离差标准化、标准差标准化和小数定标标准化。

课前预习

当然可以！下面为你详细解释离差标准化、标准差标准化和小数定标标准化，并给出简单的例子。

1. 离差标准化（Min - Max Scaling）

离差标准化是将数据缩放到[0, 1]区间的一种方法。其公式为：
[
X_{scaled} = \frac{X - X_{min}}{X_{max} - X_{min}}
]

示例：
假设有一组数据：[10, 20, 30, 40, 50]。

• 首先，找出最小值$X_{min}=10$和最大值$X_{max}=50$。
• 对于数据点10，标准化后的值为：$\frac{10-10}{50-10}=0$
• 对于数据点20，标准化后的值为：$\frac{20-10}{50-10}=0.25$
• 对于数据点30，标准化后的值为：$\frac{30-10}{50-10}=0.5$
• 对于数据点40，标准化后的值为：$\frac{40-10}{50-10}=0.75$
• 对于数据点50，标准化后的值为：$\frac{50-10}{50-10}=1$

以下是使用Python实现的代码：

import numpy as np

data = np.array([10, 20, 30, 40, 50])
min_val = data.min()
max_val = data.max()
scaled_data = (data - min_val) / (max_val - min_val)
print("离差标准化后的数据:", scaled_data)

结果

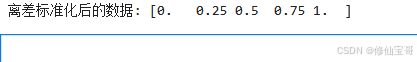
2. 标准差标准化（Standard Scaling）

标准差标准化是将数据转换为均值为0，标准差为1的标准正态分布。其公式为：
[
X_{scaled} = \frac{X - \mu}{\sigma}
]
其中，$\mu$是数据的均值，$\sigma$是数据的标准差。

示例：
假设有一组数据：[10, 20, 30, 40, 50]。

• 首先，计算均值$\mu =\frac{10+20+30+40+50}{5}=30$
• 然后，计算标准差$\sigma =\sqrt{\frac{(10-30{)}^2+(20-30{)}^2+(30-30{)}^2+(40-30{)}^2+(50-30{)}^2}{5}}\approx 14.14$
• 对于数据点10，标准化后的值为：$\frac{10-30}{14.14}\approx -1.41$
• 对于数据点20，标准化后的值为：$\frac{20-30}{14.14}\approx -0.71$
• 对于数据点30，标准化后的值为：$\frac{30-30}{14.14}=0$
• 对于数据点40，标准化后的值为：$\frac{40-30}{14.14}\approx 0.71$
• 对于数据点50，标准化后的值为：$\frac{50-30}{14.14}\approx 1.41$

以下是使用Python实现的代码：

import numpy as np

data = np.array([10, 20, 30, 40, 50])
mean_val = data.mean()
std_val = data.std()
scaled_data = (data - mean_val) / std_val
print("标准差标准化后的数据:", scaled_data)

结果

3. 小数定标标准化（Decimal Scaling）

小数定标标准化通过移动小数点的位置来进行数据缩放。其公式为：
[
X_{scaled} = \frac{X}{10^j}
]
其中，$j$是满足$10^j\ge \max (|X|)$的最小整数。

示例：
假设有一组数据：[10, 20, 30, 40, 50]。

• 首先，找出数据的绝对值的最大值$\max (|X|)=50$。
• 因为$10^2=100\ge 50$，所以$j=2$。
• 对于数据点10，标准化后的值为：$\frac{10}{10^2}=0.1$
• 对于数据点20，标准化后的值为：$\frac{20}{10^2}=0.2$
• 对于数据点30，标准化后的值为：$\frac{30}{10^2}=0.3$
• 对于数据点40，标准化后的值为：$\frac{40}{10^2}=0.4$
• 对于数据点50，标准化后的值为：$\frac{50}{10^2}=0.5$

以下是使用Python实现的代码：

import numpy as np

data = np.array([10, 20, 30, 40, 50])
j = np.ceil(np.log10(np.abs(data).max()))
scaled_data = data / (10 ** j)
print("小数定标标准化后的数据:", scaled_data)

结果

这些标准化方法在数据预处理中非常有用，可以帮助提高机器学习模型的性能。

代码整体概述

代码主要使用了pandas和numpy库，从CSV文件中读取用户每月支出信息，对数据进行清洗和预处理，然后分别使用自定义的函数对每月支出数据进行三种标准化处理，并打印出标准化前后的数据。

代码详细解析

1. 导入必要的库

import pandas as pd
import numpy as np

• 代码解释：
  • import pandas as pd：导入pandas库并将其重命名为pd，pandas是一个强大的数据处理和分析库，用于读取、处理和分析表格数据。
  • import numpy as np：导入numpy库并将其重命名为np，numpy是Python的一个科学计算库，提供了高效的数组操作和数学函数。

2. 读取数据并进行预处理

try:
    pay = pd.read_csv('./data/user_pay_info.csv', index_col=0)
    # 确保每月支出列是数值类型
    pay['每月支出'] = pd.to_numeric(pay['每月支出'], errors='coerce')
    pay = pay.dropna(subset=['每月支出'])

• 代码解释：
  • pd.read_csv('./data/user_pay_info.csv', index_col=0)：使用pandas的read_csv函数从CSV文件中读取数据，并将第一列作为索引列。
  • pd.to_numeric(pay['每月支出'], errors='coerce')：将每月支出列的数据转换为数值类型，errors='coerce'表示如果遇到无法转换的值，将其转换为NaN。
  • pay.dropna(subset=['每月支出'])：删除每月支出列中包含NaN值的行。

3. 离差标准化

    # 自定义离差标准化函数
    def min_max_scale(data):
        data = (data - data.min()) / (data.max() - data.min())
        return data

    # 对用户每月支出信息表的每月支出数据做离差标准化
    pay_min_max = min_max_scale(pay['每月支出'])
    print('离差标准化之前每月支出数据为：\n', pay['每月支出'].head())
    print('离差标准化之后每月支出数据为\n', pay_min_max.head())

• 代码解释：
  • min_max_scale函数：自定义的离差标准化函数，公式为 $x_{scaled}=\frac{x-x_{min}}{x_{max}-x_{min}}$，将数据缩放到[0, 1]区间。
  • min_max_scale(pay['每月支出'])：调用min_max_scale函数对每月支出列的数据进行离差标准化。
  • print语句：打印离差标准化前后的每月支出数据的前几行。

4. 标准差标准化

    # 自定义标准差标准化函数
    def standard_scaler(data):
        std = data.std()
        if std == 0:
            return pd.Series([0] * len(data), index=data.index)
        data = (data - data.mean()) / std
        return data

    # 对用户每月支出信息表的每月支出数据做标准差标准化
    pay_standard = standard_scaler(pay['每月支出'])
    print('标准差标准化之前每月支出数据为：\n', pay['每月支出'].head())
    print('标准差标准化之后每月支出数据为：\n', pay_standard.head())

• 代码解释：
  • standard_scaler函数：自定义的标准差标准化函数，公式为 $x_{scaled}=\frac{x-\mu }{\sigma }$，其中 $\mu$ 是数据的均值，$\sigma$ 是数据的标准差。如果标准差为0，则将所有数据置为0。
  • standard_scaler(pay['每月支出'])：调用standard_scaler函数对每月支出列的数据进行标准差标准化。
  • print语句：打印标准差标准化前后的每月支出数据的前几行。

5. 小数定标标准化

    # 自定义小数定标标准化函数
    def decimal_scaler(data):
        data = data / 10 ** np.ceil(np.log10(data.abs().max()))
        return data

    # 对用户每月支出信息表的每月支出数据做小数定标标准化
    pay_decimal = decimal_scaler(pay['每月支出'])
    print('小数定标标准化之前的每月支出数据：\n', pay['每月支出'].head())
    print('小数定标标准化之后的每月支出数据：\n', pay_decimal.head())

except FileNotFoundError:
    print("错误：未找到文件，请检查文件路径。")
except Exception as e:
    print(f"发生未知错误：{e}")

• 代码解释：
  • decimal_scaler函数：自定义的小数定标标准化函数，公式为 $x_{scaled}=\frac{x}{10^j}$，其中 $j$ 是满足 $10^j\ge \max (|x|)$ 的最小整数。
  • decimal_scaler(pay['每月支出'])：调用decimal_scaler函数对每月支出列的数据进行小数定标标准化。
  • print语句：打印小数定标标准化前后的每月支出数据的前几行。
  • except语句：捕获文件未找到错误和其他未知错误，并打印相应的错误信息。

结果

总结

通过本文的代码解析，我们学习了如何使用Python对数据进行三种常见的标准化处理：离差标准化、标准差标准化和小数定标标准化。读者在学习后能够掌握以下知识和技能：

• 学会使用pandas和numpy库进行数据读取、处理和分析。
• 理解离差标准化、标准差标准化和小数定标标准化的原理和实现方法。
• 掌握自定义函数的编写和调用，以及异常处理的方法。