目录
一·、概念
1.2方法
二、基于python的时间序列
2.1移动平均法
2.2指数平滑法
2.3灰色预测
2.4灰色关联
2.5ARIMA模型
模型系
三、 基于matlab的时间序列
3.1移动平均法
3.2指数平滑法
一次指数平滑法
二次指数平滑法
一·、概念
1.1带有时间的数据有哪些特殊性 带有时间的数据有哪些特殊性




1.2方法

二、基于python的时间序列
2.1移动平均法

import numpy as np
y=np.array([423,358,434,445,527,429,426,502,480,384,427,446])
def MoveAverage(y,N):
Mt=[' ']*N
for i in range(N+1,len(y)+2):
M=y[i-N-1:i-1].mean()
Mt.append(round(M))
return Mt
yt3=MoveAverage(y, 3)
yt5=MoveAverage(y, 5)
s3=np.sqrt(((y[3:]-yt3[3:-1])**2).mean())
s5=np.sqrt(((y[5:]-yt5[5:-1])**2).mean())
print(yt3)
print(s3)
print(yt5)
print(s5)
import pandas as pd
d=pd.DataFrame(np.c_[np.r_[y,[' ']],np.r_[yt3],np.r_[yt5]])
f=pd.ExcelWriter('move_average_example.xlsx')
d.to_excel(f)
f.close()2.2指数平滑法

import numpy as np
import pandas as pd
y=np.array([423,358,434,445,527,429,426,502,480,384,427,446])
def ExpMove(y,a):
n=len(y)
M=np.zeros(n)
#M[0]=(y[0]+y[1])/2
M[0]=y[0]
for i in range(1,len(y)):
M[i]=a*y[i-1]+(1-a)*M[i-1]
return M
yt1=ExpMove(y,0.2)
yt2=ExpMove(y,0.5)
yt3=ExpMove(y,0.8)
s1=np.sqrt(((y-yt1)**2).mean())
s2=np.sqrt(((y-yt2)**2).mean())
s3=np.sqrt(((y-yt3)**2).mean())
d=pd.DataFrame(np.c_[y,yt1,yt2,yt3])
f=pd.ExcelWriter('exp_smooth_example.xlsx')
d.to_excel(f)
f.close()
print(s1)
print(0.2*y[-1]+0.8*yt1[-1])
print(s2)
print(0.5*y[-1]+0.5*yt2[-1])
print(s3)
print(0.2*y[-1]+0.8*yt3[-1])
print(d)2.3灰色预测
概念
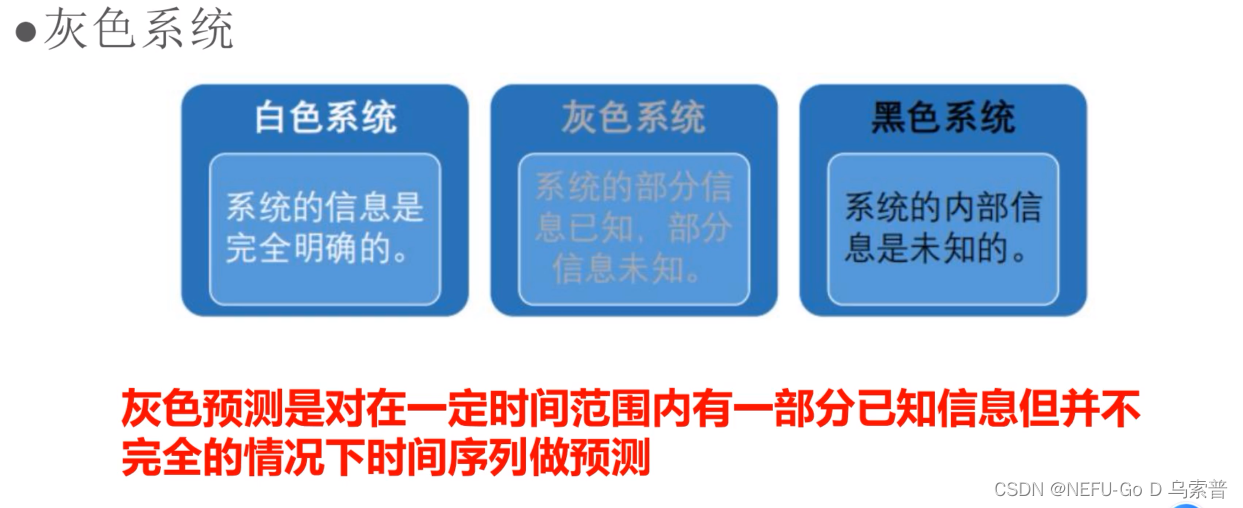
模型

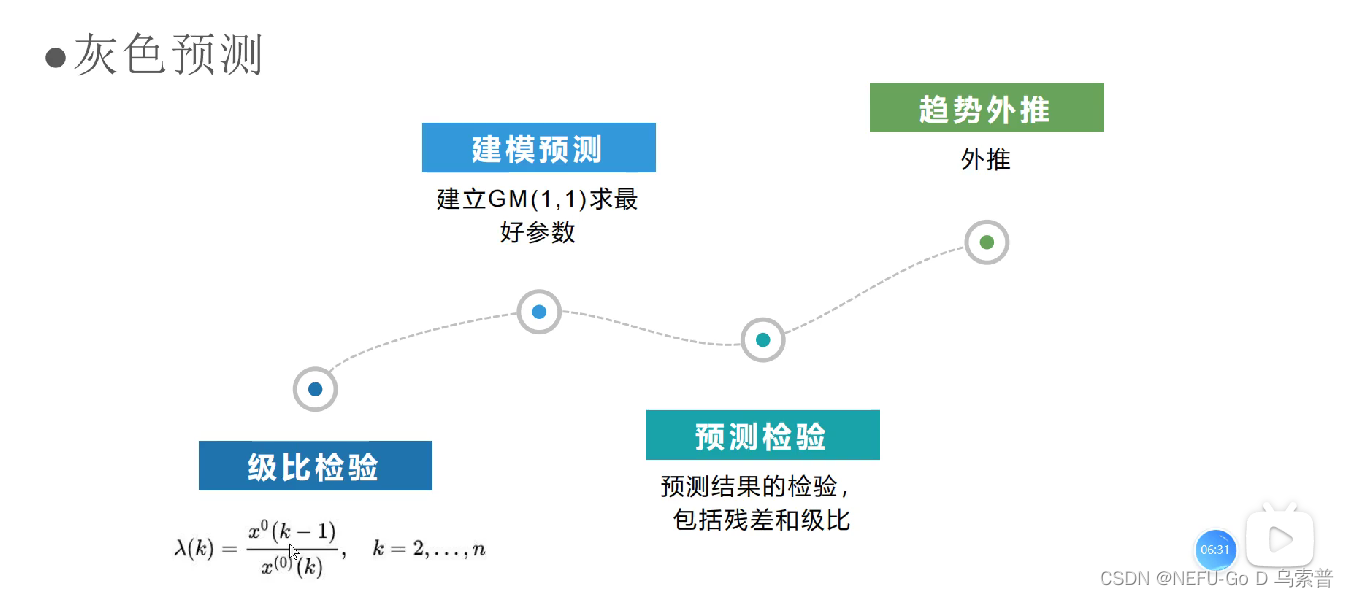
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
class GrayForecast():
#初始化
def __init__(self, data, datacolumn=None):
if isinstance(data, pd.core.frame.DataFrame):
self.data=data
try:
self.data.columns = ['数据']
except:
if not datacolumn:
raise Exception('您传入的dataframe不止一列')
else:
self.data = pd.DataFrame(data[datacolumn])
self.data.columns=['数据']
elif isinstance(data, pd.core.series.Series):
self.data = pd.DataFrame(data, columns=['数据'])
else:
self.data = pd.DataFrame(data, columns=['数据'])
self.forecast_list = self.data.copy()
if datacolumn:
self.datacolumn = datacolumn
else:
self.datacolumn = None
#save arg:
# data DataFrame 数据
# forecast_list DataFrame 预测序列
# datacolumn string 数据的含义
#级比校验
def level_check(self):
# 数据级比校验
n = len(self.data)
lambda_k = np.zeros(n-1)
for i in range(n-1):
lambda_k[i] = self.data.ix[i]["数据"]/self.data.ix[i+1]["数据"]
if lambda_k[i] < np.exp(-2/(n+1)) or lambda_k[i] > np.exp(2/(n+2)):
flag = False
else:
flag = True
self.lambda_k = lambda_k
if not flag:
print("级比校验失败,请对X(0)做平移变换")
return False
else:
print("级比校验成功,请继续")
return True
#save arg:
# lambda_k 1-d list
#GM(1,1)建模
def GM_11_build_model(self, forecast=5):
if forecast > len(self.data):
raise Exception('您的数据行不够')
X_0 = np.array(self.forecast_list['数据'].tail(forecast))
# 1-AGO
X_1 = np.zeros(X_0.shape)
for i in range(X_0.shape[0]):
X_1[i] = np.sum(X_0[0:i+1])
# 紧邻均值生成序列
Z_1 = np.zeros(X_1.shape[0]-1)
for i in range(1, X_1.shape[0]):
Z_1[i-1] = -0.5*(X_1[i]+X_1[i-1])
B = np.append(np.array(np.mat(Z_1).T), np.ones(Z_1.shape).reshape((Z_1.shape[0], 1)), axis=1)
Yn = X_0[1:].reshape((X_0[1:].shape[0], 1))
B = np.mat(B)
Yn = np.mat(Yn)
a_ = (B.T*B)**-1 * B.T * Yn
a, b = np.array(a_.T)[0]
X_ = np.zeros(X_0.shape[0])
def f(k):
return (X_0[0]-b/a)*(1-np.exp(a))*np.exp(-a*(k))
self.forecast_list.loc[len(self.forecast_list)] = f(X_.shape[0])
#预测
def forecast(self, time=5, forecast_data_len=5):
for i in range(time):
self.GM_11_build_model(forecast=forecast_data_len)
#打印日志
def log(self):
res = self.forecast_list.copy()
if self.datacolumn:
res.columns = [self.datacolumn]
return res
#重置
def reset(self):
self.forecast_list = self.data.copy()
#作图
def plot(self):
self.forecast_list.plot()
if self.datacolumn:
plt.ylabel(self.datacolumn)
plt.legend([self.datacolumn])
plt.show()
f = open("电影票房.csv", encoding="utf8")
df = pd.read_csv(f)
gf = GrayForecast(df, '票房')
gf.forecast(10)
print(gf.log())
gf.plot()
2.4灰色关联
概念

2.5ARIMA模型
序列的平稳性

判定方法

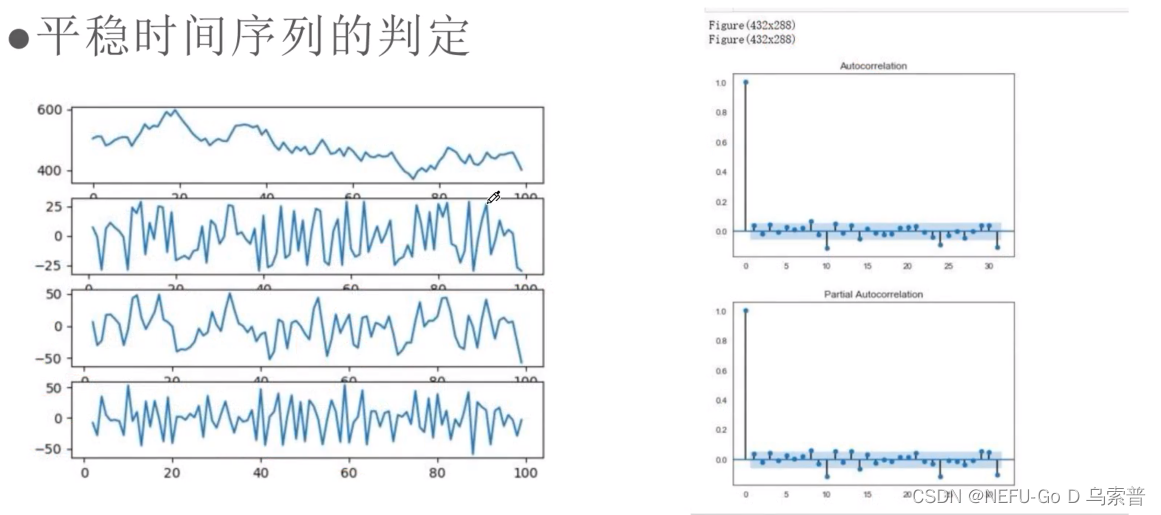
 转换
转换
差分法 比值法 取对数
模型系








例题

#导入相关库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 解决图标题中文乱码问题
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#导入数据
data=pd.read_excel('huiseguanlian.xlsx')
# print(data)
#提取变量名 x1 -- x7
label_need=data.keys()[1:]
# print(label_need)
#提取上面变量名下的数据
data1=data[label_need].values
print(data1)
#0.002~1区间归一化
[m,n]=data1.shape #得到行数和列数
data2=data1.astype('float')
data3=data2
ymin=0
ymax=1
for j in range(0,n):
d_max=max(data2[:,j])
d_min=min(data2[:,j])
data3[:,j]=(ymax-ymin)*(data2[:,j]-d_min)/(d_max-d_min)+ymin
print(data3)
# 绘制 x1,x4,x5,x6,x7 的折线图
t=range(2007,2014)
plt.plot(t,data3[:,0],'*-',c='red')
for i in range(4):
plt.plot(t,data3[:,2+i],'.-')
plt.xlabel('year')
plt.legend(['x1','x4','x5','x6','x7'])
plt.title('灰色关联分析')
plt.show()
# 得到其他列和参考列相等的绝对值
for i in range(3,7):
data3[:,i]=np.abs(data3[:,i]-data3[:,0])
#得到绝对值矩阵的全局最大值和最小值
data4=data3[:,3:7]
d_max=np.max(data2)
d_min=np.min(data2)
a=0.5 #定义分辨系数
# 计算灰色关联矩阵
data4=(d_min+a*d_max)/(data4+a*d_max)
xishu=np.mean(data4, axis=0)
print(' x4,x5,x6,x7 与 x1之间的灰色关联度分别为:')
print(xishu)三、 基于matlab的时间序列
3.1移动平均法
例题
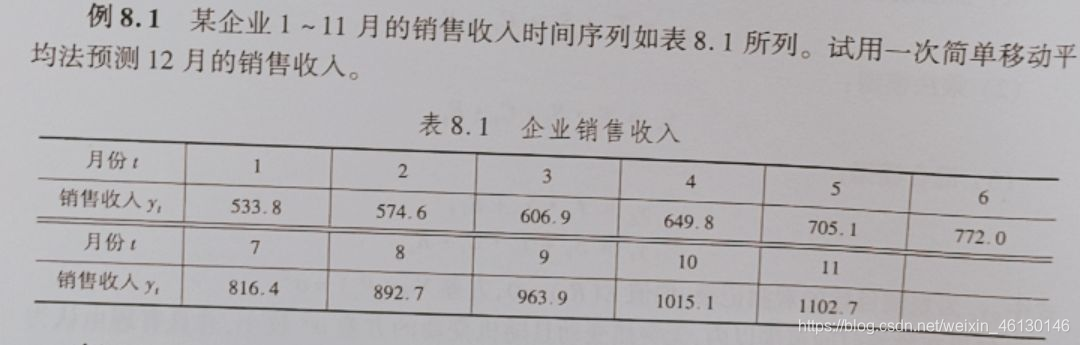

clc
clear
y = [533.8 574.6 606.9 649.8 705.1 772.0 816.4 892.7 963.9 1015.1 1102.7]
m = length(y)
n = [4 5]
for i = 1 : length(n)
for j = 1 : m - n(i) + 1
yhat{i}(j) = sum(y(j : j + n(i) - 1 ))/n(i) % 由于取得n的值不同,所以用到了细胞数组。
end
y(12) = yhat{i}(end)
s(i) = sqrt(mean((y(n(i) + 1 : end) - yhat{i}(1 : end - 1)) .^ 2))
end
3.2指数平滑法
一次移动平均实际上认为最近N期数据对未来的值的影响相同加权都是1/N,但是N期之前的数据对当前数据的预测起不到任何的作用,即加权为0。但是二次及更高次的平均权数不是1/N,而且次数越高,权数的结构越复杂。指数平滑法很有作用。
一次指数平滑法
模型
加权系数的选择
若α = 0, 则 yt+1hat = ythat, 就是下期的预测值等于本期的预测值。
那么对于α的选择尤为重要
(1)如果时间序列波动变化不大,比较平稳,那么阿尔法取小点0.1-0.5之间,以减少修正的幅度。
(2)若具有迅速明显的变动倾向,阿尔法取大些,0.6-0.8,使得灵敏度高些,以便于跟得上速度的变化。
现实中可以选择多个数据进行比较。
初始值的确定
一般情况下,可以去前10%的数据的均值开确定初始值。
例题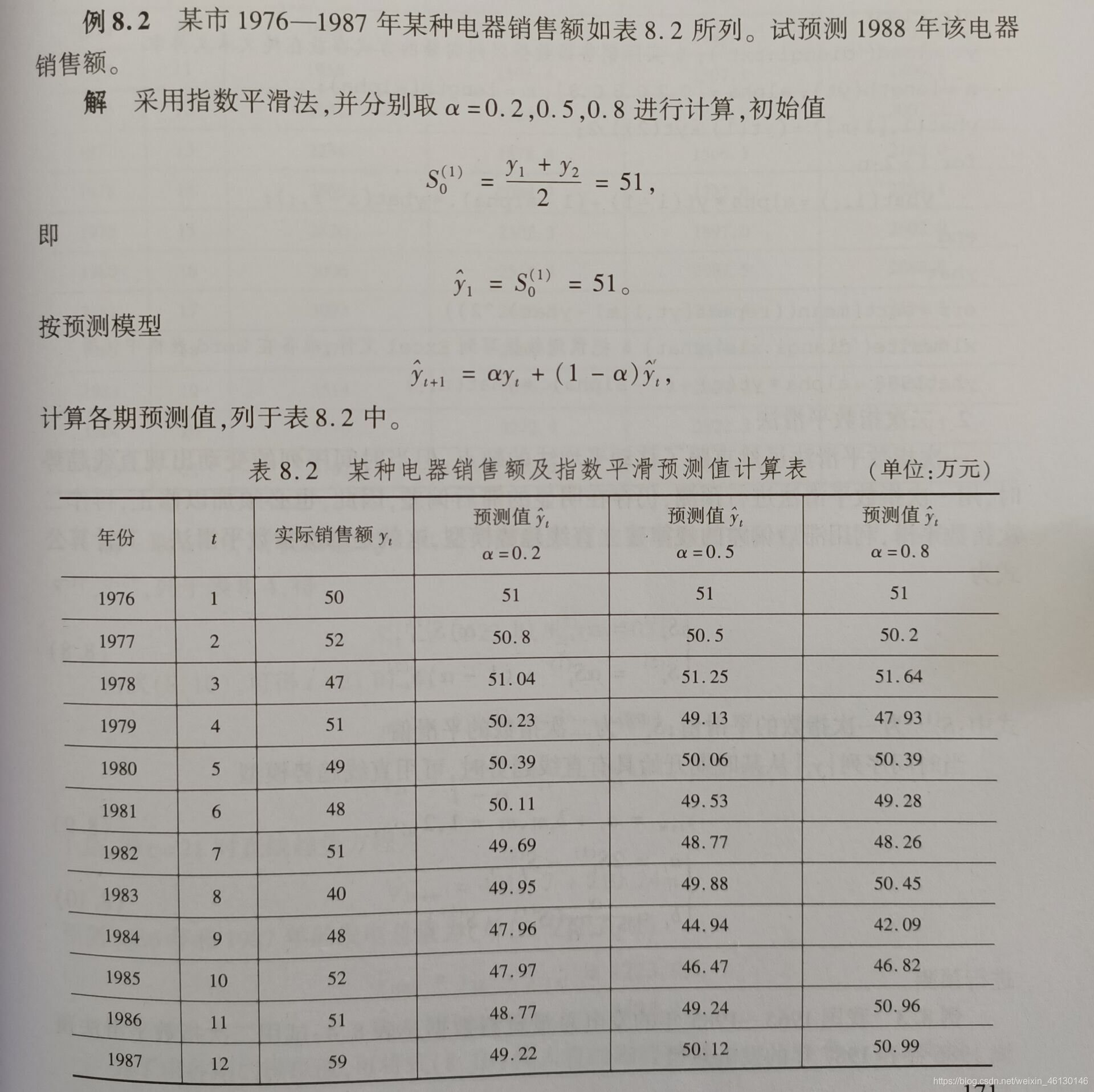
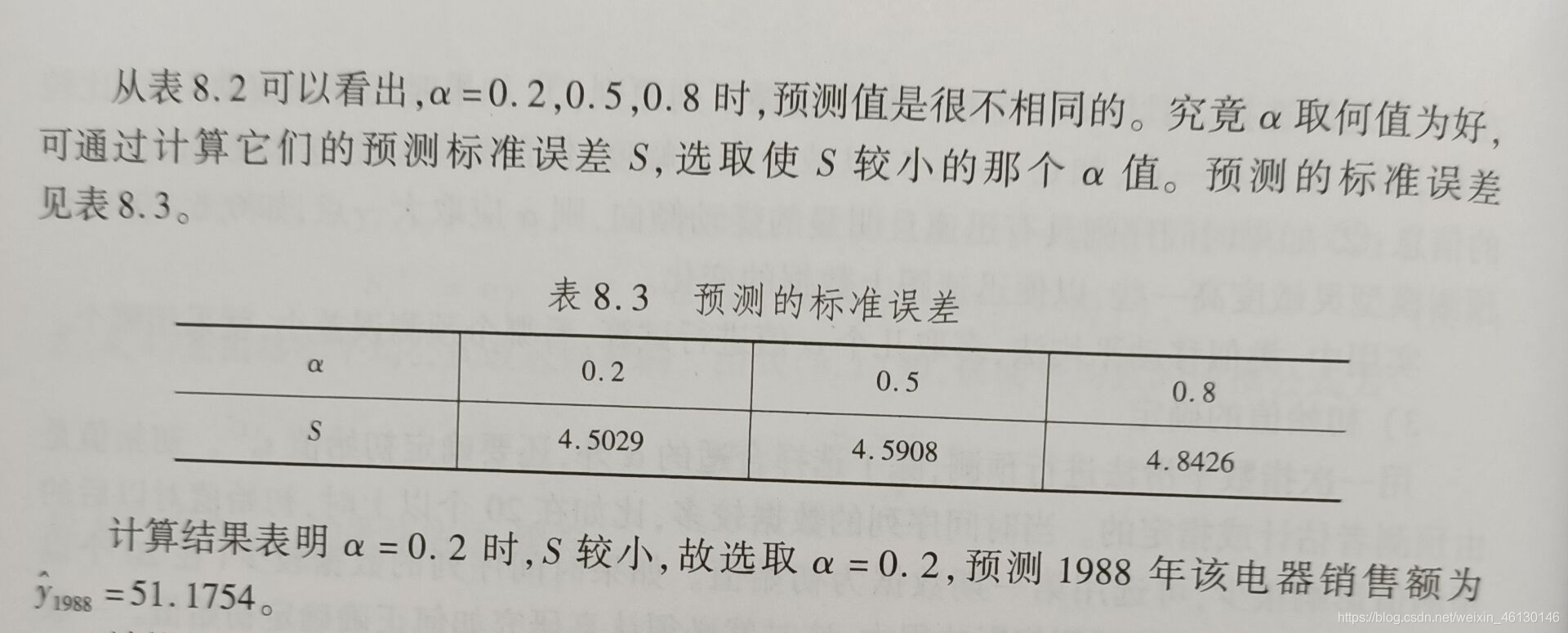
clc
clear
yt = load('doanqi.txt')
n = length(yt)
alpha = [0.2 0.5 0.8]
m = length(alpha)
yhat (1, [1 : m])= (yt(1) + yt(2)) / 2;
for i = 2 : n
yhat(i, :) = alpha * yt(i - 1) + (1 - alpha) .* yhat( i - 1, : )
end
yhat
err = sqrt(mean((repmat(yt, 1, m) - yhat) .^ 2 ))
二次指数平滑法
一次指数平滑法,虽然克服了移动平均法的缺点,但是当时间序列的变动出现直线趋势时,用一次指数平滑法就会存在明显的滞后偏差,因此也必须要加以修正再做二次指数平滑,利用滞后偏差的规律建立直线趋势模型,就是所谓的二次指数平滑法。
例题

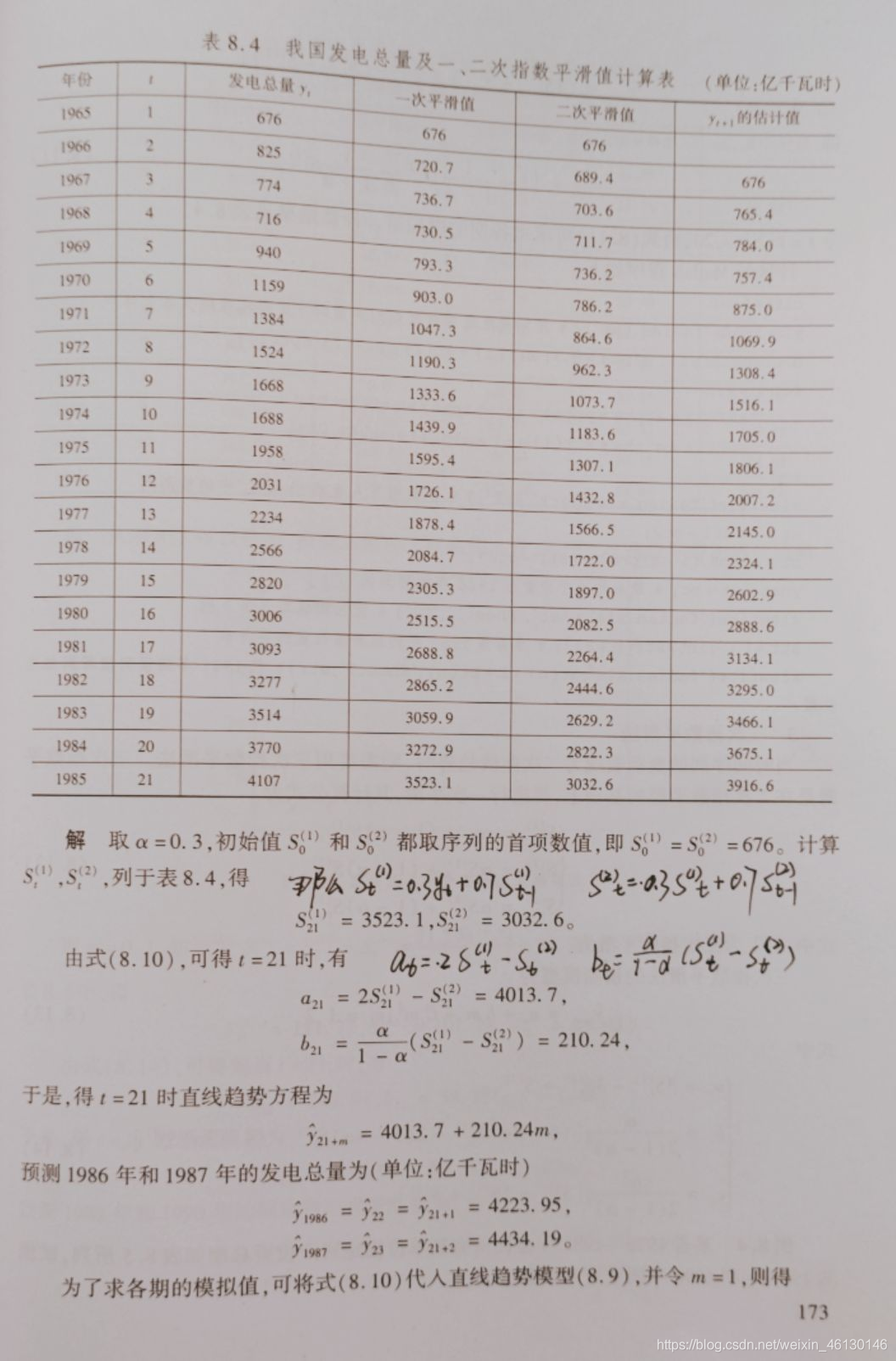
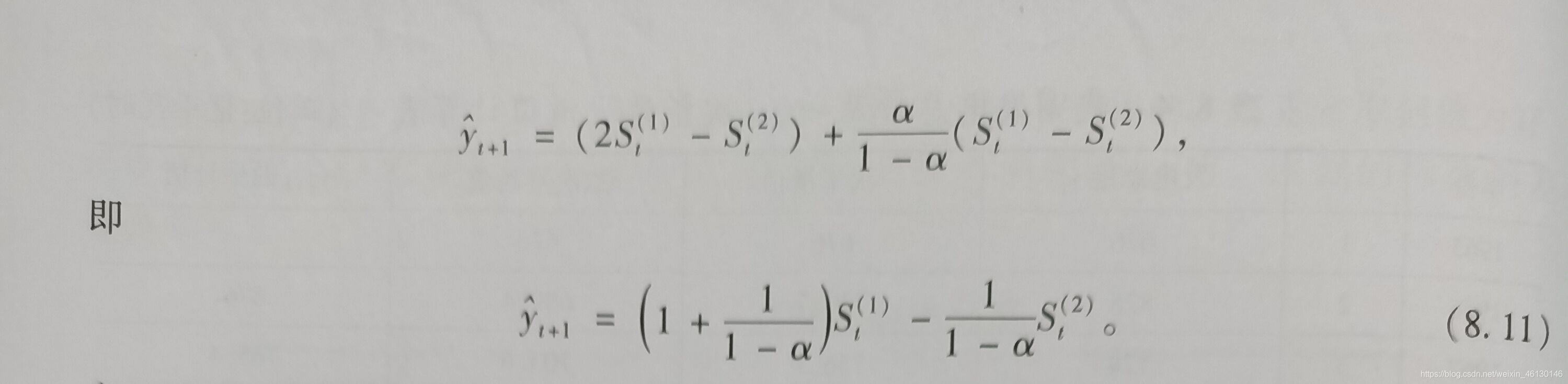
clc
clear
yt = load('fadian.txt')
n = length(yt); alpja = 0.3; st1(1) = yt(1); st2(1) = yt(1)
for i = 2 : n
st1(i) = alpha * yt(i) + ( 1 - alpha ) * st1( i - 1 )
st2(i) = alpha * st1(i) + (1 - alpha) * st2(i - 1)
end
at = 2*st1 - st2
bt = alpha/(1 - alpha)*(st1 - st2)
yhat = at + bt
str = ['C', int2str(n+2)];