来源:力扣(LeetCode)
描述:
有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。
最开始时:
- 「一号」玩家从
[1, n]中取一个值x(1 <= x <= n); - 「二号」玩家也从
[1, n]中取一个值y(1 <= y <= n)且y != x。
「一号」玩家给值为 x 的节点染上红色,而「二号」玩家给值为 y 的节点染上蓝色。
之后两位玩家轮流进行操作,「一号」玩家先手。每一回合,玩家选择一个被他染过色的节点,将所选节点一个 未着色 的邻节点(即左右子节点、或父节点)进行染色(「一号」玩家染红色,「二号」玩家染蓝色)。
如果(且仅在此种情况下)当前玩家无法找到这样的节点来染色时,其回合就会被跳过。
若两个玩家都没有可以染色的节点时,游戏结束。着色节点最多的那位玩家获得胜利 ✌️。
现在,假设你是「二号」玩家,根据所给出的输入,假如存在一个 y 值可以确保你赢得这场游戏,则返回 true ;若无法获胜,就请返回 false 。
示例 1 :
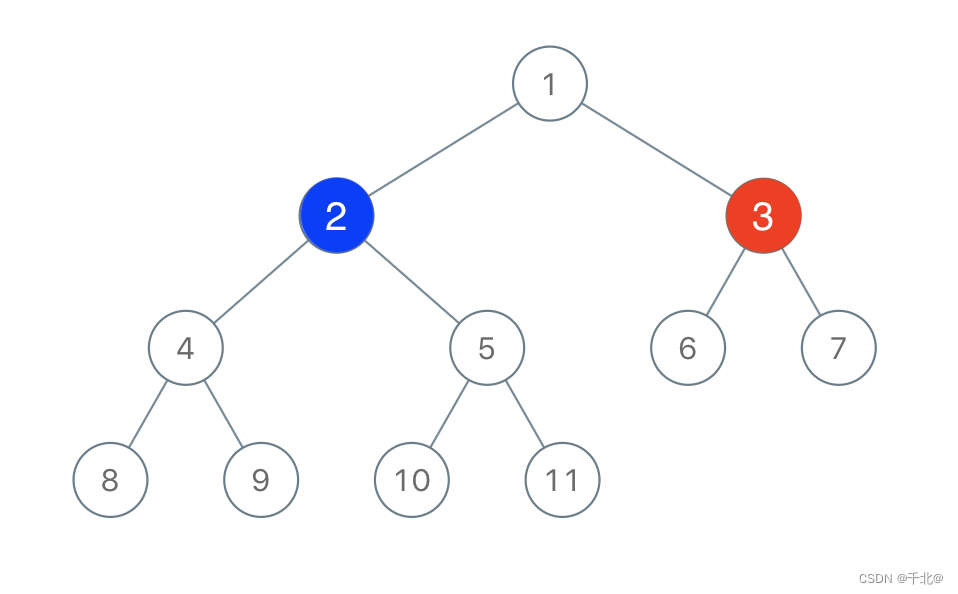
输入:root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
输出:true
解释:第二个玩家可以选择值为 2 的节点。
示例 2 :
输入:root = [1,2,3], n = 3, x = 1
输出:false
提示:
- 树中节点数目为 n
- 1 <= x <= n <= 100
- n 是奇数
- 1 <= Node.val <= n
- 树中所有值 互不相同
方法:深度优先搜索
由于二叉树中的每个节点的值各不相同,因此可以根据节点值唯一地确定二叉树中的节点。
在 n 个节点的二叉树中,节点 x 将二叉树分成三个区域:节点 x 的左子树、节点 x 的右子树和其余节点,三个区域的节点总数是 n − 1,每个区域可能为空。
根据游戏规则,一号玩家首先选择节点 x 着色,之后每次选择的节点必须和一号玩家已经着色的节点相邻,因此一号玩家第二次选择的节点一定是节点 x 的父节点、左子节点或右子节点,每个可以选择的节点分别属于不同的区域。
由于一号玩家已经选择节点 x 着色,因此二号玩家只能在三个区域中选择一个节点着色,且之后二号玩家只能在相同的区域选择节点着色。二号玩家的目标是使自己着色的节点数大于一号玩家着色的节点数,因此二号玩家应使自己着色的节点数最大化,二号玩家的策略如下。
- 二号玩家应选择节点数最多的区域中的一个节点着色。
- 对于选定的区域,二号玩家应使自己在该区域中着色的节点数最大化,着色的最大节点数应等于该区域的节点数,因此二号玩家应避免一号玩家在该区域中选择节点着色。为了做到这一点,二号玩家应选择该区域中与节点 x 相邻的节点着色,此时一号玩家无法在该区选择节点着色,二号玩家可以从首次选择着色的节点开始将该区域的所有节点着色。
根据策略,二号玩家应选择节点数最多的区域中的一个节点着色,二号玩家着色的节点数等于该区域的节点数。
由于二号玩家只能选择一个区域着色,因此其余两个区域和节点 x 都将由一号玩家着色,二叉树中的所有节点都将被其中一个玩家着色。如果一个玩家着色的节点数超过半数,则该玩家获胜。
二叉树中有 n 个节点,n 是奇数,如果一个玩家着色的节点数不少于 (n+1) / 2 ,则该玩家着色的节点数超过半数,该玩家获胜。
为了判断二号玩家是否可以获胜,需要分别计算三个区域的节点数。如果存在一个区域的节点数不少于 (n+1) / 2,则二号玩家可以选择该区域着色并获胜;如果三个区域的节点数都少于 (n+1) / 2,则无论二号玩家选择哪个区域,可以着色的节点数都将少于半数,此时一号玩家可以着色的节点数超过半数,一号玩家获胜。
代码:
class Solution {
public:
bool btreeGameWinningMove(TreeNode* root, int n, int x) {
TreeNode* xNode = find(root, x);
int leftSize = getSubtreeSize(xNode->left);
if (leftSize >= (n + 1) / 2) {
return true;
}
int rightSize = getSubtreeSize(xNode->right);
if (rightSize >= (n + 1) / 2) {
return true;
}
int remain = n - 1 - leftSize - rightSize;
return remain >= (n + 1) / 2;
}
TreeNode* find(TreeNode *node, int x) {
if (node == NULL) {
return NULL;
}
if (node->val == x) {
return node;
}
TreeNode* res = find(node->left, x);
if (res != NULL) {
return res;
} else {
return find(node->right, x);
}
}
int getSubtreeSize(TreeNode *node) {
if (node == NULL) {
return 0;
}
return 1 + getSubtreeSize(node->left) + getSubtreeSize(node->right);
}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:10.4 MB, 在所有 C++ 提交中击败了80.00%的用户
复杂度分析
时间复杂度:O(n),其中 n 是二叉树的节点数。需要遍历二叉树寻找节点 x 和计算节点 x 的左右子树的节点数,每个节点最多访问一次。
空间复杂度:O(n),其中 n 是二叉树的节点数。空间复杂度主要是递归调用栈空间,取决于二叉树的高度,平均情况是 O(logn),最坏情况是 O(n)。
author:LeetCode-Solution