LeetCode 583. 两个字符串的删除操作
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
视频讲解![]() https://www.bilibili.com/video/BV1we4y157wB/?spm_id_from=333.788&vd_source=f98f2942b3c4cafea8907a325fc56a48文章讲解
https://www.bilibili.com/video/BV1we4y157wB/?spm_id_from=333.788&vd_source=f98f2942b3c4cafea8907a325fc56a48文章讲解![]() https://programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html
https://programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html
- 思路:
- 思路一:求最长公共子序列的长度,同LeetCode 1143.最长公共子序列
- dp[i][j]:word1的子串[0, i - 1] 与 word2的子串[0, j - 1] 的最长公共子序列的长度
- 最终结果:word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()]
- 思路二:
- dp[i][j]:令 word1的子串[0, i - 1] 与 word2的子串[0, j - 1] 相同所需的最小步数
- 递推公式:
- word1[i - 1] 与 word2[j - 1]相同:dp[i][j] = dp[i - 1][j - 1]; 都不用删
- word1[i - 1] 与 word2[j - 1]不同:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);删掉其中一个(两个都删包含在删一个里面了)
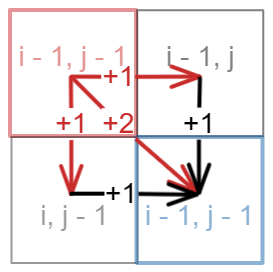
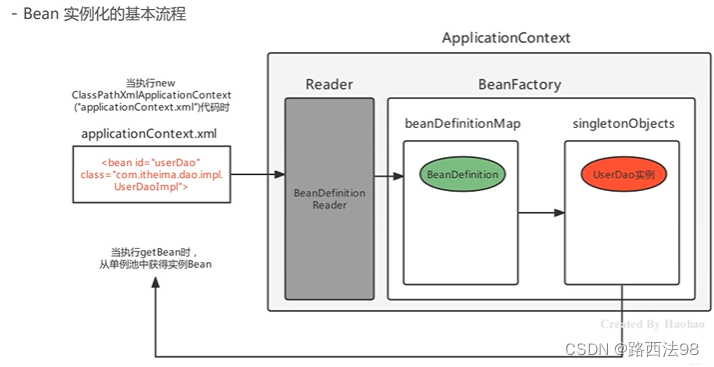
状态转移图
- 初始化:
- 令 word1[0, i-1] 和 空串 相同所需的最小步数👉dp[i][0] = i
- 同理 dp[0][j] = j
- 遍历顺序:从上到下,从左到右
- 最终结果:dp[word1.size()][word2.size()]
- 思路一:求最长公共子序列的长度,同LeetCode 1143.最长公共子序列
- 代码:
// 思路一:最长公共子序列的长度
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1, 0));
for (int i=1; i<=word1.size(); i++){
for (int j=1; j<=word2.size(); j++){
if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return word1.size()+word2.size()-dp[word1.size()][word2.size()]*2;
}
};// 思路二:最小步数
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[word1.size()][word2.size()];
}
};LeetCode 72. 编辑距离
给你两个单词 word1 和 word2,请返回将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
视频讲解![]() https://www.bilibili.com/video/BV1qv4y1q78f/?spm_id_from=333.788&vd_source=f98f2942b3c4cafea8907a325fc56a48文章讲解
https://www.bilibili.com/video/BV1qv4y1q78f/?spm_id_from=333.788&vd_source=f98f2942b3c4cafea8907a325fc56a48文章讲解![]() https://programmercarl.com/0072.%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB.html
https://programmercarl.com/0072.%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB.html
- 思路:
- dp[i][j]:将 word1的子串[0, i - 1] 转换成 word2的子串[0, j - 1] 所需的最小操作数
- 递推公式:
- word1[i - 1] 与 word2[j - 1]相同:dp[i][j] = dp[i - 1][j - 1]; 不用操作
- word1[i - 1] 与 word2[j - 1]不同:
- dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
-
将 word1的子串[0, i - 2] 转换成 word2的子串[0, j - 2],再替换 word1[i - 1] 为 word2[j - 1]👉dp[i - 1][j - 1] + 1
-
将 word1的子串[0, i - 2] 转换成 word2的子串[0, j - 1],再删除 word1[i - 1]👉dp[i - 1][j] + 1
-
将 word1的子串[0, i - 1] 转换成 word2的子串[0, j - 2],再插入 word2[j - 1]👉dp[i][j - 1] + 1
- 初始化:
- 将 word1[0, i-1] 转换成 空串 所需的最小操作数👉dp[i][0] = i(删除所有字符)
- 同理 dp[0][j] = j(将 空串 转换成 word2[0, j-1])
- 遍历顺序:从上到下,从左到右
- 最终结果:dp[word1.size()][word2.size()]
- 代码:
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
}
}
return dp[word1.size()][word2.size()];
}
};编辑距离总结篇
判断子序列:s 是否为 t 的子序列
不同的子序列:计算在 s 的子序列中 t 出现的个数
两个字符串的删除操作:令 word1 和 word2 相同所需的最小步数(只能删除)
编辑距离:将 word1 转换成 word2 所需的最小操作数(三种操作:替换、删除、插入)










![[NeurIPS 2018] Hyperbolic neural networks](https://img-blog.csdnimg.cn/8027b3fc89a242449675127ee2f7fe99.png#pic_center)