3. 具体例子

3.1-3.3都只需要用第一章concave-convex方法求解，3.4-3.6需要用到第二章的拉格朗日对偶变换，而且具体解$\mathbf{x}$时需要对离散变量单独开发算法。

3.1 多小区SISO能量分配

第一个例子是具有一组单天线基站（BSs）$\mathcal{B}$的下行链路SISO蜂窝网络的经典功率控制问题，每个基站服务于单天线用户。设$h_{i,j}\in$C是从BS
j到用户i的下行链路信道；设${\sigma }^2$为加性高斯白噪声（AWGN）功率电平。为每个BS i引入可变$p_i$作为其发射功率电平，受Pmax功率预算的约束。第i个用户的速率

$$R_i=\log \left(1+\frac{|h_{i,i}{|}^2{p}_i}{{\sum }_{j\ne i}|h_{i,j}{|}^2{p}_j+{\sigma }^2}\right)$$

优化问题如下。

$$\begin{array}{rl}\underset{\mathbf{p}}{\mathrm{maximize}}& f_o(\mathbf{p})=\sum _{i\in \mathcal{B}}{w}_i{R}_i\\ \text{subject to}& 0\le p_i\le P_{\max },\forall i\in \mathcal{B}.\end{array}$$

先说明，对于两种等效方法，都可以使用简单的初始值，比如能量平均分配。此问题可以拓展到多载波$R_i={\sum }_{t=1}^T\frac{1}{T}\log \left(1+\frac{|h_{i,i}^t{|}^2{p}_i^t}{{\sum }_{j\ne i}|h_{i,j}^t{|}^2{p}_j^t+{\sigma }^2}\right)$

3.1.1 Direct FP

对log里面的分数项做处理，得到直接FP形式如下。直接使用算法1，可以得到$y_i^{\star }=\frac{\sqrt{A_m(\mathbf{x})}}{B_m(\mathbf{x})}=\frac{\sqrt{|h_{i,i}{|}^2{p}_i}}{{\sum }_{j\ne i}|h_{i,j}{|}^2{p}_j+{\sigma }^2}$，代入后用数值方法求解p（剩下的是凸问题），然后迭代。
$$f_q^{\text{DIR}}(\mathbf{p},\mathbf{y})=\sum _{i\in \mathcal{B}}{w}_i\log (1+2y_i\sqrt{|h_{i,i}{|}^2{p}_i}-y_i^2(\sum _{j\ne i}|h_{i,j}{|}^2{p}_j+{\sigma }^2))$$

进一步地，只要目标函数（或叫做效用函数）$U_i$是关于$R_i$的nondecreasing concave函数，都可以对$R_i$里面的分数项使用二次变换等效。

3.1.2 拉格朗日对偶变换求闭式解

应用第二部分的拉格朗日对偶变换方法，首先得到下式，

$$f_r^{\text{CF}}(\mathbf{p},\mathbf{\gamma })=\sum _{i\in \mathcal{B}}{w}_i\log \left(1+{\gamma }_i\right)-\sum _{i\in \mathcal{B}}{w}_i{\gamma }_i+\sum _{i\in \mathcal{B}}\frac{w_i(1+{\gamma }_i)|h_{i,i}{|}^2{p}_i}{{\sum }_{j\in \mathcal{B}}|h_{i,j}{|}^2{p}_j+{\sigma }^2}$$

上式引入辅助变量的最优解为${\gamma }_i^{\star }=\frac{A_m(\mathbf{x})}{B_m(\mathbf{x})}=\frac{|h_{i,i}{|}^2{p}_i}{{\sum }_{j\ne i}|h_{i,j}{|}^2{p}_j+{\sigma }^2}$，再对最后一项分数项做二次变换，$f_r$的前两项记为$\text{const}(\mathbf{\gamma })$

$$f_q^{\text{CF}}(\mathbf{p},\mathbf{\gamma },\mathbf{y})=\sum _{i\in \mathcal{B}}2y_i\sqrt{w_i(1+{\gamma }_i)|h_{i,i}{|}^2{p}_i}-\sum _{i\in \mathcal{B}}{y}_i^2(\sum _{j\in \mathcal{B}}|h_{i,j}{|}^2{p}_j+{\sigma }^2)+\text{const}(\mathbf{\gamma })$$

上式引入辅助变量的最优解为$y_i^{\star }=\frac{\sqrt{A_m(\mathbf{x})}}{B_m(\mathbf{x})}=\frac{\sqrt{w_i(1+{\gamma }_i)|h_{i,i}{|}^2{p}_i}}{{\sum }_{j\in \mathcal{B}}|h_{i,j}{|}^2{p}_j+{\sigma }^2},\forall i\in \mathcal{B}.$，然后$f_q$对$p$求导，再结合约束条件中$p<P_{\max }$，即可解得

$$p_i^{\star }=\min \{P_{\max },\frac{y_i^2{w}_i(1+{\gamma }_i)|h_{i,i}{|}^2}{({\sum }_{j\in \mathcal{B}}{y}_j^2|h_{j,i}{|}^2{)}^2}\},\forall i\in \mathcal{B}$$

最后，${\gamma }_i^{\star },y_i^{\star },p_i^{\star }$依次迭代，可收敛到最优值。

自行推导$p_i^{\star }$：首先可以得到$f_q$中关于$p_i$的一项为：
$$f_{q,i}=2y_i\sqrt{w_i(1+{\gamma }_i)|h_{i,i}{|}^2}\sqrt{p_i}-\sum _{j\in \mathcal{B}}{y}_j^2|h_{j,i}{|}^2\cdot p_i$$
注意$f_q$后面一项要拆分再合并才得到$f_{q,i}$的后面一项。此时$f_{q,i}=c_1\sqrt{p_i}/2-c_2\cdot p_i$，令$\partial f_{q,i}/\partial p_i=c_1/\sqrt{p_i}/2-c_2=0$，则$p_i=(c_1/c_2/4{)}^2$，就是上式。

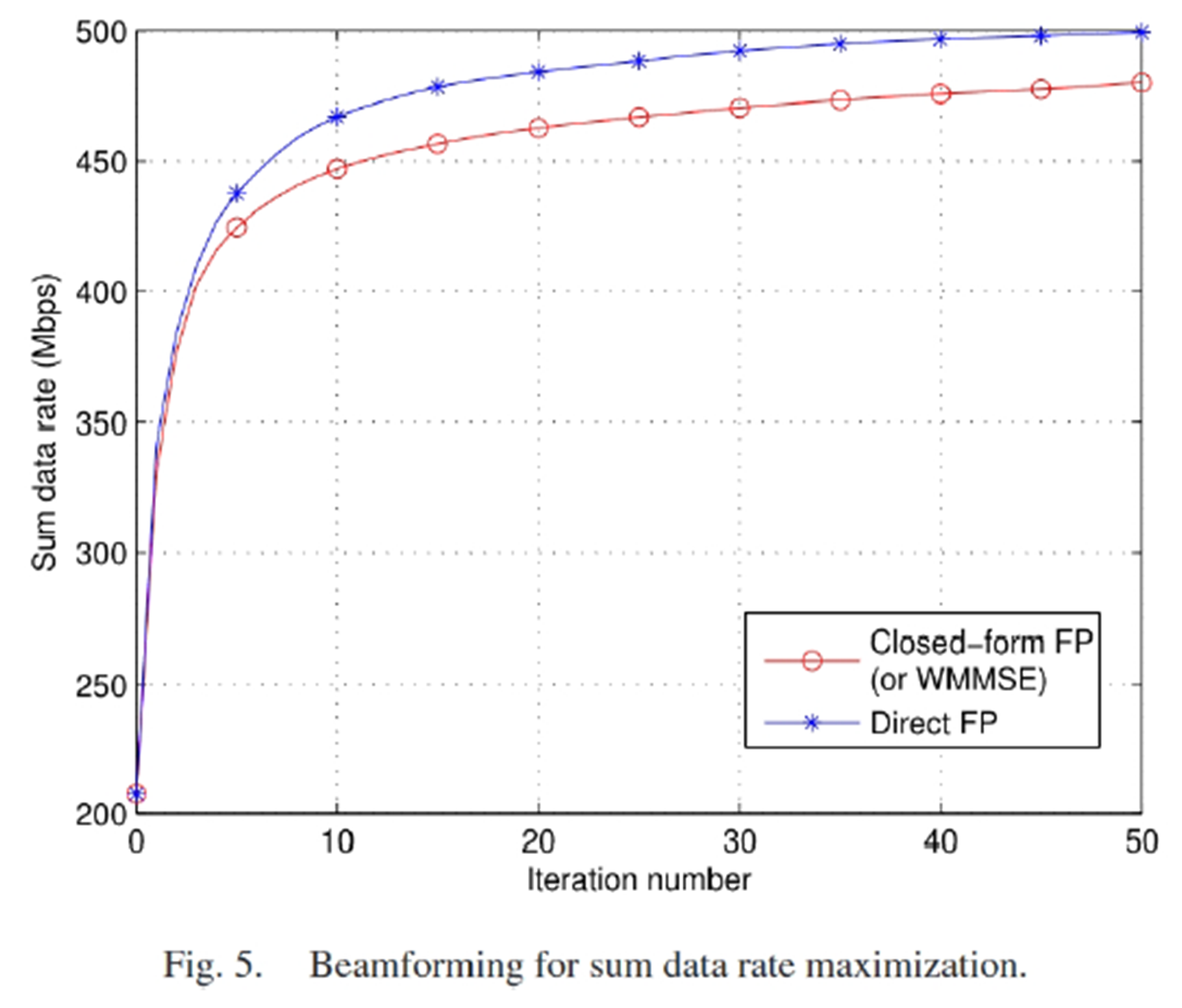
3.1.3 结果比较

图中的SCALE是一个modified version of geometric programming (GP)[32].
要注意，SCALE每次迭代要用数值法解一个GP问题，Direct FP每次迭代要用数值法解一个关于p的凸优化问题，牛顿法中有比较复杂的公式和一部分搜索，而闭式解FP则全是解析解。虽然所提的FP方法需要迭代数多，但复杂度还是要更低的。在作者的测试中，closed-form
FP最快收敛完成。从结果上看，依靠数值法求解的SCALE和Direct FP能得到更好的性能。

• [32] J. Papandriopoulos and J. S. Evans, “SCALE: A low-complexity
  distributed protocol for spectrum balancing in multiuser DSL networks,”
  IEEE Trans. Inf. Theory, vol. 55, no. 8, pp. 3711–3724, Jul. 2009

3.2 多小区MIMO beamforming

考虑具有一组BS $\mathcal{B}$的下行链路MIMO蜂窝网络。假设每个BS具有M个天线，并且每个用户终端具有N个天线；则经由空间复用每个小区最多支持M个下行链路数据流。设${\mathbf{H}}_{im,j}\in {\mathbb{C}}^{N\times M}$是从$[BSj]$到 $[BSi]$的第m个数据流中调度的用户的下行链路信道。设σ2是AWGN功率电平。引入变量${\mathbf{v}}_{im}\in {\mathbb{C}}^M$作为其第m个数据流在BS
i处的下行链路发射波束形成器。流（i，m）的数据速率如下

$$R_{im}(\mathbf{V})=\log (1+{\mathbf{v}}_{im}^{†}{\mathbf{H}}_{im,i}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)\ne (i,m)}{\mathbf{H}}_{im,j}{\mathbf{v}}_{jn}{\mathbf{v}}_{jn}^{†}{\mathbf{H}}_{im,j}^{†}{)}^{-1}{\mathbf{H}}_{im,i}{\mathbf{v}}_{im})$$

令$\mathbf{V}$代表所有的 { v i m } \{\mathbf{v}_{im}\} {vim​}，加入权重之后，优化问题如下

$$\begin{array}{rl}\underset{\mathbf{V}}{\mathrm{maximize}}& \sum _{i,m}{w}_{im}{R}_{im}(\mathbf{V})\\ \text{subject to}& \sum _{m=1}^M\Vert {\mathbf{v}}_{im}{\Vert }_2^2\le P_{\max },\forall i\in \mathcal{B}\end{array}$$

3.2.1 Direct FP

使用1.4节中的方法，做二次变换，得到

$$f_q^{\text{DIR}}(\mathbf{V},\mathbf{Y})=\sum _{(i,m)}{w}_{im}\log (1+2\text{Re}\left\{{\mathbf{y}}_{im}^{†}{\mathbf{H}}_{im,i}{\mathbf{v}}_{im}\right\}-{\mathbf{y}}_{im}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)\ne (i,m)}{\mathbf{H}}_{im,j}{\mathbf{v}}_{jn}{\mathbf{v}}_{jn}^{†}{\mathbf{H}}_{im,j}^{†}\left){\mathbf{y}}_{im}\right)$$

根据${\mathbf{y}}_m^{\star }=({\mathbf{B}}_m(\mathbf{x}){)}^{-1}{\mathbf{a}}_m(\mathbf{x})$，得到下式。然后数值法求解二次变换后的等效问题（关于V是凸问题），迭代求解。

$${\mathbf{y}}_{im}^{\star }=({\sigma }^2\mathbf{I}+\sum _{(j,n)\ne (i,m)}{\mathbf{H}}_{im,j}{\mathbf{v}}_{jn}{\mathbf{v}}_{jn}^{†}{\mathbf{H}}_{im,j}^{†}{)}^{-1}{\mathbf{H}}_{im,i}{\mathbf{v}}_{im}$$

3.2.2 拉格朗日对偶变换求闭式解

与3.1.2类似，只不过是矩阵形式的。首先通过拉格朗日对偶得到$f_r$，再对内部的分式做二次变换得到$f_q$.

$$f_r^{\text{CF}}(\mathbf{V},\mathbf{\gamma })=\sum _{(i,m)}{w}_{im}(\log (1+{\gamma }_{im})-{\gamma }_{im}+(1+{\gamma }_{im}){\mathbf{v}}_{im}^{†}{\mathbf{H}}_{im,i}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)}{\mathbf{H}}_{im,j}{\mathbf{v}}_{jn}{\mathbf{v}}_{jn}^{†}{\mathbf{H}}_{im,j}^{†}{)}^{-1}{\mathbf{H}}_{im,i}{\mathbf{v}}_{im})$$

$${\gamma }_{im}^{\star }={\mathbf{v}}_{im}^{†}{\mathbf{H}}_{im,i}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)\ne (i,m)}{\mathbf{H}}_{im,j}{\mathbf{v}}_{jn}{\mathbf{v}}_{jn}^{†}{\mathbf{H}}_{im,j}^{†}{)}^{-1}{\mathbf{H}}_{im,i}{\mathbf{v}}_{im}$$

f q CF ( V , γ , Y ) = ∑ ( i , m ) ( 2 w i m ( 1 + γ i m )    Re { v i m † H i m , i † y i m } − y i m † ( σ 2 I + ∑ ( j , n ) H i m , j v j n v j n † H i m , j † ) y i m ) + const ( γ ) f_{q}^{\text{CF}}(\mathbf{V},\boldsymbol{\gamma},\mathbf{Y})=\sum_{(i,m)}\Bigg(2\sqrt{w_{im}(1+\gamma_{im})}\;\text{Re}\lbrace\mathbf{v}_{im}^{\dagger}\mathbf{H}_{im,i}^{\dagger}\mathbf{y}_{im}\rbrace-\mathbf{y}_{im}^{\dagger}\Bigg(\sigma^{2}\mathbf{I}+\sum_{(j,n)}\mathbf{H}_{im,j}\mathbf{v}_{jn}\mathbf{v}_{jn}^{\dagger}\mathbf{H}_{im,j}^{\dagger}\Bigg)\mathbf{y}_{im}\Bigg)+\text{const}(\boldsymbol{\gamma}) fqCF​(V,γ,Y)=(i,m)∑​(2wim​(1+γim​) ​Re{vim†​Him,i†​yim​}−yim†​(σ2I+(j,n)∑​Him,j​vjn​vjn†​Him,j†​)yim​)+const(γ)

$${\mathbf{y}}_{im}^{\star }=({\sigma }^2\mathbf{I}+\sum _{(j,n)}{\mathbf{H}}_{im,j}{\mathbf{v}}_{jn}{\mathbf{v}}_{jn}^{†}{\mathbf{H}}_{im,j}^{†}{)}^{-1}\cdot \sqrt{w_{im}(1+{\gamma }_{im})}{\mathbf{H}}_{im,i}{\mathbf{v}}_{im}$$

$${\mathbf{v}}_{im}^{\star }=({\eta }_i\mathbf{I}+\sum _{(j,n)}{\mathbf{H}}_{jn,i}^{†}{\mathbf{y}}_{jn}{\mathbf{y}}_{jn}^{†}{\mathbf{H}}_{jn,i}{)}^{-1}\cdot \sqrt{w_{im}(1+{\gamma }_{im})}{\mathbf{H}}_{im,i}^{†}{\mathbf{y}}_{im}$$

注意${\mathbf{v}}_{im}^{\star }$中还有一个变量${\eta }_i$，${\eta }_i$是为功率约束引入的对偶变量，由（互补松弛）最优确定。文章说这个值可以由二分搜索等方法得到，应该是把${\eta }_i$代入上式，

$${\eta }_i^{\star }=\min \left\{{\eta }_i\ge 0:\sum _{m=1}^M\Vert {\mathbf{v}}_{im}({\eta }_i){\Vert }_2^2\le P_{\max }\right\}$$

需要注意的是，此方法和WMMSE等效算法得到的结果是一致的。与前面类似，Direct FP可以得到更好的性能，而Closed-form
FP可以得到更低复杂度。

自行推导${\mathbf{v}}_{im}^{\star }$：与3.1.2类似，注意矩阵求导$\partial {\mathbf{b}}^T{\mathbf{X}}^T\mathbf{Xc}/\partial \mathbf{X}=\mathbf{X}(\mathbf{b}{\mathbf{c}}^T+\mathbf{c}{\mathbf{b}}^T)$，则$\partial {\mathbf{b}}^T{\mathbf{X}}^T\mathbf{Xb}/\partial \mathbf{X}=2\mathbf{b}{\mathbf{b}}^T\mathbf{X}$.
${\eta }_i$是在求解${\mathbf{v}}_{im}^{\star }$时，把约束考虑进来之后，构造出来的拉格朗日对偶问题引入的辅助变量。
对于约束${\sum }_{m=1}^M\Vert {\mathbf{v}}_{im}{\Vert }_2^2\le P_{\max }$，可写为${\sum }_{m=1}^M{\mathbf{v}}_{im}^{†}{\mathbf{v}}_{im}-P_{\max }\le 0$，即 t r { V i † V i } − P max ⁡ ≤ 0 \mathrm{tr}\{\mathbf{V}_{i}^{\dagger}\mathbf{V}_{i}\}-P_{\max}\leq0 tr{Vi†​Vi​}−Pmax​≤0，
构造出
f q , v CF ( V , γ , Y ) = f q CF ( V , γ , Y ) − ∑ i η i ( t r { V i † V i } − P max ⁡ ) f_{q,v}^{\text{CF}}(\mathbf{V},\boldsymbol{\gamma},\mathbf{Y})=f_{q}^{\text{CF}}(\mathbf{V},\boldsymbol{\gamma},\mathbf{Y})-\sum_{i}\eta_{i}\left(\mathrm{tr}\{\mathbf{V}_{i}^{\dagger}\mathbf{V}_{i}\}-P_{\max}\right) fq,vCF​(V,γ,Y)=fqCF​(V,γ,Y)−i∑​ηi​(tr{Vi†​Vi​}−Pmax​)
添加的对偶项求导后为$2{\eta }_i{\mathbf{V}}_i$.

3.3 能效最大化

跨多个干扰链路的能效最大化是一个更具挑战性的问题。考虑一个空间复用多天线广播信道模型，其中一个发送器配备有M个天线，以向其M个接收器发送单独的数据。假设每个接收机具有N个天线并且支持一个数据流。设${\mathbf{H}}_m\in {\mathbb{C}}^{N\times M}$是发送方和第M个接收方之间的信道；设${\mathbf{v}}_m\in {\mathbb{C}}^M$是用于传输到第m个接收器的波束形成器。$P_{on}$是电路的固定功耗。在这种情况下，能源效率最大化问题如下

$$\begin{array}{rl}\underset{\mathbf{V}}{\mathrm{maximize}}& \frac{{\sum }_{m=1}^M{R}_m(\mathbf{V})}{{\sum }_{m=1}^M\Vert {\mathbf{v}}_m{\Vert }_2^2+P_{\text{on}}}\\ \text{subject to}& \sum _{m=1}^M\Vert {\mathbf{v}}_m{\Vert }_2^2\le P_{\max }\end{array}$$

$$R_m(\mathbf{V})=\log (1+{\mathbf{v}}_m^{†}{\mathbf{H}}_m^{†}({\sigma }^2\mathbf{I}+\sum _{n\ne m}{\mathbf{H}}_m{\mathbf{v}}_n{\mathbf{v}}_n^{†}{\mathbf{H}}_m^{†}{)}^{-1}\cdot {\mathbf{H}}_m{\mathbf{v}}_m)$$

这个问题里，目标函数是一个分式，而$R_m$内部又是一个分式，直接使用两次二次变换等效，使用Direct FP方法求解。仿真表明，在单链路问题下，可以收敛到和Dinkelbach等效方法一致的结果，多链路时Dinkelbach方法不适用。

3.4 多小区SISO上行调度和能量分配

考虑无线蜂窝网络的上行链路，B是部署在网络中的基站（BSs）集合，${\mathcal{K}}_i$是与BS i关联的用户集合，每个BS
i及其在${\mathcal{K}}_i$中的关联用户构成一个小区。在每个时隙中，用户被调度为基于小区的上行链路传输。为了用户调度和功率控制的目的，引入变量$s_i\in {\mathcal{K}}_i$表示在BS
i调度的用户，如果用户$k$被调度为上行链路传输，则引入变量$p_k$表示其发射功率电平。设$h_{i,k}\in \mathbb{C}$是从用户k到BS
i的上行信道系数。关于$s_i$的理解，SISO场景，基站i一个时刻只能与一个设备通信，$s_i$就是这个设备的编号？比如基站1对设备5，基站2对设备6，那么$s_1=5,s_2=6$
？由于上行链路调度决策对干扰模式有重要影响，即小区i中的特定调度决策si强烈影响其相邻小区中的调度决策sj，因此这个问题很难直接解决。为什么直接讨论拉格朗日对偶变换法（性能比direct
FP差点），因为想得到更多的解析式来讨论？

maximize s ,   p   f o ( s , p ) = ∑ i ∈   B w s i log ⁡ ( 1 + ∣ h i , s i ∣ 2 p s i ∑ j ≠ i ∣ h i , s j ∣ 2 p s j + σ 2 ) subject to   0 ≤ p k ≤ P max ⁡ , s i ∈ K i ∪ { ∅ } \begin{aligned}\underset{\mathbf{s},\,\mathbf{p}}{\text{maximize}}\quad\ & f_{o}(\mathbf{s},\mathbf{p})=\sum_{i\in\,\mathcal{B}}w_{s_{i}}\log\left(1+\frac{|h_{i,s_{i}}|^{2}p_{s_{i}}}{\sum_{j\ne i}|h_{i,s_{j}}|^{2}p_{s_{j}}+\sigma^{2}}\right)\\ \text{subject to}\quad\ & 0\leq p_{k}\leq P_{\max},\quad s_{i}\in\mathcal{K}_{i}\cup\lbrace\varnothing\rbrace \end{aligned} s,pmaximize​ subject to ​fo​(s,p)=i∈B∑​wsi​​log(1+∑j=i​∣hi,sj​​∣2psj​​+σ2∣hi,si​​∣2psi​​​)0≤pk​≤Pmax​,si​∈Ki​∪{∅}​

一种经典的等效方法是
$$f_o(\mathbf{p})=\sum _{i\in \mathcal{B}}\sum _{k\in {\mathcal{K}}_i}{w}_k\log (1+\frac{|h_{i,k}{|}^2{p}_k}{{\sum }_{k^{\prime }\ne k}|h_{i,k^{\prime }}{|}^2{p}_{k^{\prime }}+{\sigma }^2})$$
主要问题是，由于目标函数的高度非凸性，功率控制算法的驻点对初始条件高度敏感。因此，这类方法存在严重的过早停止问题。如果某个环节在迭代优化的早期阶段被停用，那么它就永远无法在以后的迭代中被重新激活，因为它的局部梯度会强烈阻碍它这样做。使用GP的方法[30]可以改善这点，但只能在高SINR下工作，但是在小区干扰场景中，SINR往往较低。
使用拉格朗日对偶变换：
$$f_r(\mathbf{s},\mathbf{p},\mathbf{\gamma })=\sum _{i\in \mathcal{B}}{w}_{s_i}\log \left(1+{\gamma }_i\right)-\sum _{i\in \mathcal{B}}{w}_{s_i}{\gamma }_i+\sum _{i\in \mathcal{B}}\frac{w_{s_i}({\gamma }_i+1)|h_{i,s_i}{|}^2{p}_{s_i}}{{\sum }_j|h_{i,s_j}{|}^2{p}_{s_j}+{\sigma }^2}$$

与前面的步骤一样，${\gamma }_i^{\star }=\frac{|h_{i,s_i}{|}^2{p}_{s_i}}{{\sum }_{j\ne i}|h_{i,s_j}{|}^2{p}_{s_j}+{\sigma }^2}$，再对$f_r$分数项做二次变换$f_q$，$y_i^{\star }=\frac{\sqrt{w_{s_i}(1+{\gamma }_i)|h_{i,s_i}{|}^2{p}_{s_i}}}{{\sum }_{j\in \mathcal{B}}|h_{i,s_j}{|}^2{p}_{s_j}+{\sigma }^2}$，也可求得$p_k^{\star }=\min \left\{P_{\max },\frac{w_k(1+{\gamma }_i){|h_{i,k}|}^2{y}_i^2}{{\left({\sum }_{j\in \mathcal{B}}{|h_{j,k}|}^2{y}_j^2\right)}^2}\right\},\forall k\in {\mathcal{K}}_i$.

$$f_q(\mathbf{s},\mathbf{p},\mathbf{\gamma },\mathbf{y})=\sum _{i\in \mathcal{B}}{w}_{s_i}\log (1+{\gamma }_i)-\sum _{i\in \mathcal{B}}{w}_{s_i}{\gamma }_i+\sum _{i\in \mathcal{B}}(2y_i\sqrt{w_{s_i}({\gamma }_i+1){\left|h_{i,s_i}\right|}^2{p}_{s_i}}-y_i^2(\sum _{j\in \mathcal{B}}{\left|h_{i,s_j}\right|}^2{p}_{s_j}+{\sigma }^2\left)\right)$$

重写成如下形式，可以看到问题被解耦，具体地说，“每个小区中的调度和功率优化，即（$s_i$，$p_i$），可以在每个小区中独立地完成。即当γ和y固定时，si的优化不依赖于其他sj变量。”（不是很理解，$y$和$\gamma$的取值不是还和$s_j$有关么？也不算完全解耦，只是这个式子里确实只关注$s_i$就行，而且计算$p_k^{\star }$的时候也不用关注$s_i$是哪个。）下式也可以看做一个总的效用函数，$G_i(k)(其中计算时k\in {\mathcal{K}}_i)$是在BS
i处调度用户k的效用增益，而$D_j(k)(其中计算时k\notin {\mathcal{K}}_j)$则是通过调度用户k干扰相邻小区j的惩罚。即遍历计算每个用户$k$的总效用，选最大就完成了$s_i$的优化，不需要对所有$(s_1,s_2,...)$调度组合做搜索，复杂度大大降低。在实际应用中，可以使用两阶段调度策略来降低该算法的实现复杂度。我们首先根据潜在用户的权重粗略地选择其子集，然后应用算法对调度决策进行细化。

$$f_q(\mathbf{s},\mathbf{p},\mathbf{\gamma },\mathbf{y})=\sum _{i\in \mathcal{B}}(\underset{G_i(s_i)}{\underbrace{w_{s_i}\log (1+{\gamma }_i)-w_{s_i}{\gamma }_i-y_i^2{\sigma }^2+2y_i\sqrt{w_{s_i}({\gamma }_i+1){\left|h_{i,s_i}\right|}^2{p}_{s_i}}}}-\sum _{j\in \mathcal{B}}\underset{D_j(s_i)}{\underbrace{y_j^2{\left|h_{j,s_i}\right|}^2{p}_{s_i}}})$$

$$s_i^{\star }=\{\begin{array}{ll}\varnothing ,& \text{if}{\max }_{k\in {\mathcal{K}}_i}\{G_i(k)-{\sum }_{j\ne i}{D}_j(k)\}\le 0\\ \arg {\max }_{k\in {\mathcal{K}}_i}& \{G_i(k)-{\sum }_{j\ne i}{D}_j(k)\},\text{otherwise}\end{array}$$

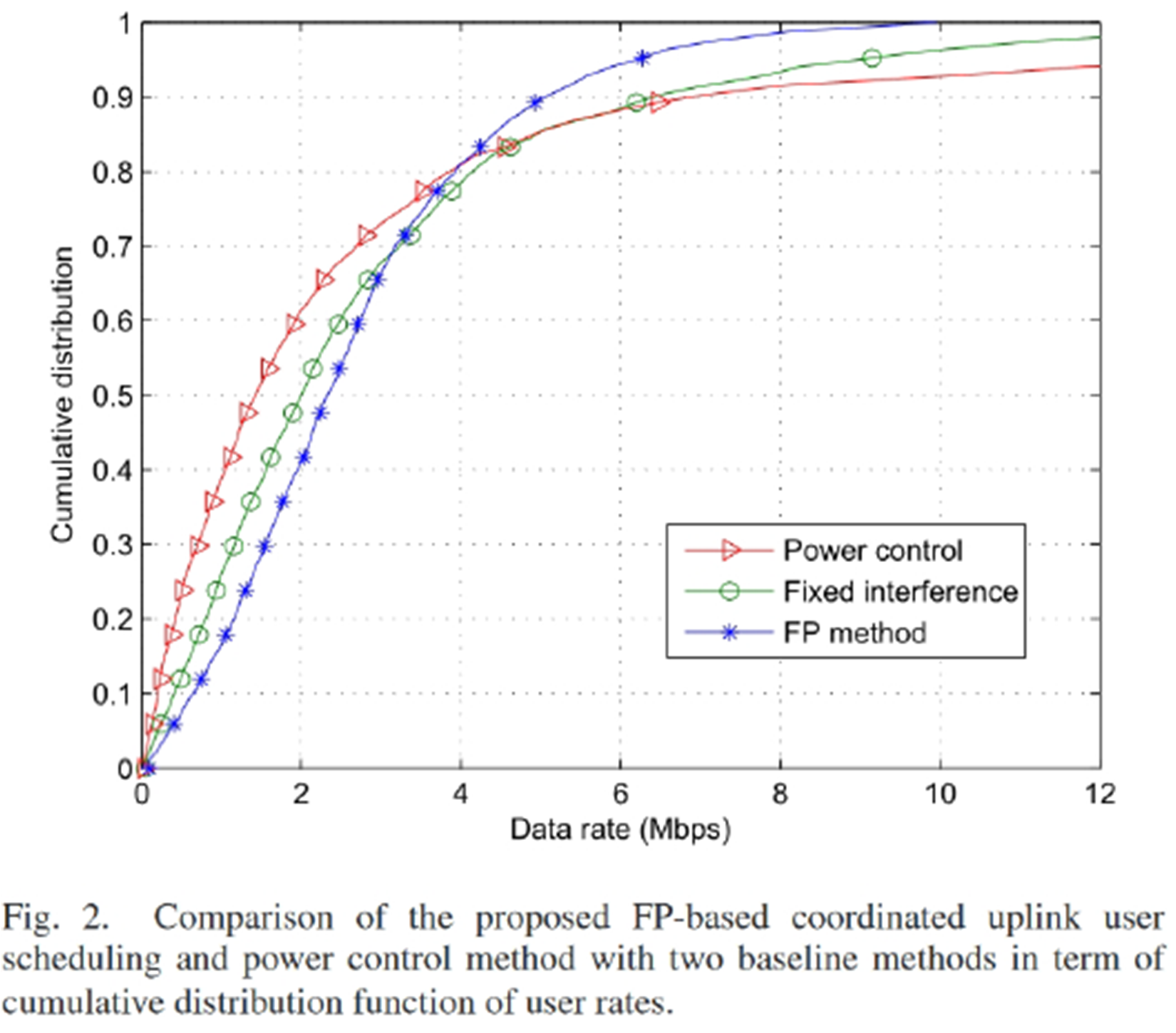
结果：曲线有交叉，怎么就说明FP好了呢？ 主要看低速率的。比如横着看，CDF=0.1时，即对最差的10%用户，FP方法对应的data
rate约1Mbps，而Power control约0.5Mbps，FP更保障了这部分差用户的性能。竖着看，速率为2Mbps（按照CDF定义，此处的值表示有多少用户低于此速率），FP只有40%用户，而Power
control有60%用户，FP处于低速率的用户更少，因此更好。而对于最好的20%用户（4Mbps+），FP确实要差一些。但文章还提供了一个表，总速率的性能（总效用函数），FP大幅优于旧方法。

3.5 多小区MIMO上行调度和beamforming

假设每个用户配备有N个天线，并且每个BS配备有M个天线。因此，空间复用可以支持每个小区多达M个数据流（但是一些数据流可能具有零吞吐量）。设s_{im}是在BS
i的第m个流中调度的用户的索引。如果用户k得到调度，则设${\mathbf{v}}_k\in {\mathbb{C}}^N$是用户k的发送波束形成器。设${\mathbf{H}}_{i,k}\in {\mathbb{C}}^{M\times N}$是从用户k到BS
i的上行链路信道。

maximize s ,   V   f o ( s , V subject to   ∥ v i m ∥ 2 2 ≤ P max ⁡   s i m ∈ K i ∪ { ∅ } \begin{aligned}\underset{\mathbf{s},\,\mathbf{V}}{\text{maximize}}\quad\ & f_{o}(\mathbf{s},\mathbf{V} \text{subject to}\quad\ & \Vert\mathbf{v}_{im}\Vert_{2}^{2}\leq P_{\max}\\ \quad\ & s_{im}\in\mathcal{K}_{i}\cup\lbrace\varnothing\rbrace \end{aligned} s,Vmaximize​  ​fo​(s,Vsubject to sim​∈Ki​∪{∅}​∥vim​∥22​≤Pmax​​

$$f_o(\mathbf{s},\mathbf{V})=\sum _{(i,m)}{w}_{s_{im}}\log \left(1+{\mathbf{v}}_{s_{im}}^{†}{\mathbf{H}}_{i,s_{im}}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)\ne (i,m)}{\mathbf{H}}_{i,s_{jn}}{\mathbf{v}}_{s_{jn}}{\mathbf{v}}_{s_{jn}}^{†}{\mathbf{H}}_{i,s_{jn}}^{†}{)}^{-1}{\mathbf{H}}_{i,s_{im}}{\mathbf{v}}_{s_{im}}\right)$$

问题比较直观，也和3.2与3.4那样先做两次变换，其中
$${\gamma }_{im}^{\star }={\mathbf{v}}_{s_{im}}^{†}{\mathbf{H}}_{i,s_{im}}^{†}{\left({\sigma }^2\mathbf{I}+\sum _{(j,n)\ne (i,m)}{\mathbf{H}}_{i,s_{jn}}{\mathbf{v}}_{s_{jn}}{\mathbf{v}}_{s_{jn}}^{†}{\mathbf{H}}_{i,s_{jn}}^{†}\right)}^{-1}{\mathbf{H}}_{i,s_{im}}{\mathbf{v}}_{s_{im}}$$

$${\mathbf{y}}_{im}^{\star }=({\sigma }^2\mathbf{I}+\sum _{(j,n)}{\mathbf{H}}_{i,s_{jn}}{\mathbf{v}}_{s_{jn}}{\mathbf{v}}_{s_{jn}}^{†}{\mathbf{H}}_{i,s_{jn}}^{†}{)}^{-1}\cdot \sqrt{w_{s_{im}}(1+{\gamma }_{im})}{\mathbf{H}}_{i,s_{im}}{\mathbf{v}}_{s_{im}}$$

$$f_r(\mathbf{s},\mathbf{V},\gamma )=\sum _{(i,m)}{w}_{s_{im}}(\log (1+{\gamma }_{im})-{\gamma }_{im}+(1+{\gamma }_{im}){\mathbf{v}}_{s_{im}}^{†}{\mathbf{H}}_{i,s_{im}}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)}{\mathbf{H}}_{i,s_{jn}}{\mathbf{v}}_{s_{jn}}{\mathbf{v}}_{s_{jn}}^{†}{\mathbf{H}}_{i,s_{jn}}^{†}{)}^{-1}{\mathbf{H}}_{i,s_{im}}{\mathbf{v}}_{s_{im}})$$

$$f_q(\mathbf{s},\mathbf{V},\gamma ,\mathbf{Y})=\sum _{(i,m)}{w}_{s_{im}}\log (1+{\gamma }_{im})-\sum _{(i,m)}{w}_{s_{im}}{\gamma }_{im}+\sum _{(i,m)}(2\sqrt{w_{s_{im}}(1+{\gamma }_{im})}\mathrm{Re}\left\{{\mathbf{v}}_{s_{im}}^{†}{\mathbf{H}}_{i,s_{im}}^{†}{\mathbf{y}}_{im}\right\}-{\mathbf{y}}_{im}^{†}({\sigma }^2\mathbf{I}+\sum _{(j,n)}{\mathbf{H}}_{i,s_{jn}}{\mathbf{v}}_{s_{jn}}{\mathbf{v}}_{s_{jn}}^{†}{\mathbf{H}}_{i,s_{jn}}^{†}){\mathbf{y}}_{im})$$

接下来的问题又是$\mathbf{s}$和$\mathbf{V}$的优化问题。将加权二部匹配的思想引入到这两个变量的联合优化中。首先，由$f_q$可以看出，特定数据流$(i,m)$的$s_{im}$和${\mathbf{v}}_{im}$与其他流的s和v优化是独立的（类似SISO问题中的“解耦”）。如果某个用户$k$在数据流$(i,m)$中被调度，即$s_{im}=k$，则用户$k$关于$(i,m)$的最优发射波束形成器可通过$\partial f_q/\partial {\mathbf{v}}_{s_{im}}=0$求得，表示为${\tau }_{k,im}$，

$${\mathbf{\tau }}_{k,im}=(\sum _{(j,n)}{\mathbf{H}}_{j,k}^{†}{\mathbf{y}}_{jn}{\mathbf{y}}_{jn}^{†}{\mathbf{H}}_{j,k}+{\eta }_{k,im}^{\star }\mathbf{I}{)}^{-1}\cdot \sqrt{w_k(1+{\gamma }_{im})}{\mathbf{H}}_{i,k}^{†}{\mathbf{y}}_{im}$$

与3.2中的问题类似，由于约束的引入，多了个${\eta }_{k,im}^{\star }$，通过二分搜索求解 η k , i m ⋆ = min ⁡ { η k , i m ≥ 0 : ∥ τ k , i m ( η k , i m ) ∥ 2 2 ≤ P max ⁡ } \eta_{k,im}^{\star}=\min\lbrace\eta_{k,im}\geq0:\Vert\boldsymbol{\tau}_{k,im}(\eta_{k,im})\Vert_{2}^{2}\leq P_{\max}\rbrace ηk,im⋆​=min{ηk,im​≥0:∥τk,im​(ηk,im​)∥22​≤Pmax​}

类似3.4节，根据$f_q$先定义一个将用户$k$分配给数据流$(i,m)$的效用函数:
$${\xi }_{k,im}=w_k\log (1+{\gamma }_{im})-w_k{\gamma }_{im}+2\sqrt{w_k(1+{\gamma }_{im})}\text{Re}\left\{{\mathbf{\tau }}_{k,im}^{†}{\mathbf{H}}_{i,k}^{†}{\mathbf{y}}_{im}\right\}-{\sigma }^2\Vert {\mathbf{y}}_{im}{\Vert }_2^2-\sum _{(j,n)}{\mathbf{y}}_{jn}^{†}{\mathbf{H}}_{j,k}{\mathbf{\tau }}_{k,im}{\mathbf{\tau }}_{k,im}^{†}{\mathbf{H}}_{j,k}^{†}{\mathbf{y}}_{jn}$$
然后，fq最大化问题简化为以下加权二分匹配问题（背包问题），其中二进制变量$x_{k,im}$表示用户$k$是否调度在数据流(i,m)中。每个用户只能用一个流，每个流只能调度一个用户。通过使用例如匈牙利算法[6]和拍卖算法[7]的具有多项式时间计算复杂度的现有算法，计算复杂度为$O((K+M{)}^3)$。此外，由于在实践中，匹配权重ξk，im总是以有限精度进行评估，因此在这种有限精度的情况下，可以使用[34]中的算法将匹配的复杂度降低到$O((K+M{)}^2)$.

maximize x   ∑ k ∈   K i ∑ m = 1 N ξ k , i m x k , i m subject to   ∑ k ∈   K i x k , i m ≤ 1 ,    ∀ m   ∑ m = 1 N x k , i m ≤ 1 ,    ∀ k   x k , i m ∈ { 0 , 1 } , \begin{aligned}\underset{\mathbf{x}}{\text{maximize}}\quad\ & \sum_{k\in\,\mathcal{K}_{i}}\sum_{m=1}^{N}\xi_{k,im}x_{k,im}\\ \text{subject to}\quad\ & \sum_{k\in\,\mathcal{K}_{i}}x_{k,im}\leq1,\;\forall m\\ \quad\ & \sum_{m=1}^{N}x_{k,im}\leq1,\;\forall k\\ \quad\ & x_{k,im}\in\left\lbrace 0,1\right\rbrace , \end{aligned} xmaximize​ subject to   ​k∈Ki​∑​m=1∑N​ξk,im​xk,im​k∈Ki​∑​xk,im​≤1,∀mm=1∑N​xk,im​≤1,∀kxk,im​∈{0,1},​

如果考虑预编码权值是离散的，考虑码本
$$\mathcal{V}=\left\{{\mathbf{\varphi }}_1,{\mathbf{\varphi }}_2,\cdots ,{\mathbf{\varphi }}_{|\mathcal{V}|}\right\}$$
其中${\mathbf{\varphi }}_n\in {\mathbb{C}}^N$为一个特定预编码。此时，用户$k$关于$(i,m)$的最优预编码改为（可通过搜索得到，复杂度$O(|V|))$

$${\mathbf{\tau }}_{k,im}=\arg \underset{\mathbf{v}\in \mathcal{V}}{\max }\left\{2\sqrt{w_k(1+{\gamma }_{im})}\text{Re}\left\{{\mathbf{v}}^{†}{\mathbf{H}}_{i,k}^{†}{\mathbf{y}}_{im}\right\}-\sum _{(j,n)}{\mathbf{y}}_{jn}^{†}{\mathbf{H}}_{j,k}\mathbf{v}{\mathbf{v}}^{†}{\mathbf{H}}_{j,k}^{†}{\mathbf{y}}_{jn}\right\}$$

再用背包问题求解，也是一样的。如果先按老方法优化，然后找一个距离最近的波束，即${\mathbf{\tau }}_{k,im}=\arg {\min }_{\mathbf{\varphi }\in \mathcal{V}}\Vert \mathbf{\varphi }-{\tilde{\mathbf{v}}}_{im}{\Vert }_2$，这样能降低复杂度到$O(log|V|)$，虽然看上去是启发式的搜索，但论文里证明了能到最优。

再然后就是和WMMSE方法的比较，对信道差的用户提供的速率比WMMSE好，总效用函数高10%。在K>>M的情况下，WMMSE有更高的communication complexity。在K>>M和N的情况下，FP方法的计算复杂度也要更低（特别是使用更高效的背包问题求解方法后）。

往期精选：

• 毫米波大规模MIMO的AOA估计

• 线性降维：主成分分析PCA原理分析与仿真验证

• 5G+AI：有哪些新的研究方向和新范式？

• 简述3D点云配准算法

• 5G为人工智能与工业互联网赋能|79页高清PPT

• 智能算法|以动物命名的算法

• 一份超全面的机器学习公共数据集

• 矩阵填充|奇异值阈值算法

• 可重构/大规模智能反射表面reconfigurable/large intelligent surface综述

• 迭代硬阈值类算法总结||IHT/NIHT/CGIHT/HTP

• 软阈值迭代算法（ISTA）和快速软阈值迭代算法（FISTA）

• 伍德伯里矩阵恒等式（Woodbury matrix identity）

• 压缩感知：一种新型亚采样技术

更多精彩内容请关注订阅号优化与算法和加入QQ讨论群1032493483获取更多资料