系列文章目录

·【算法系列】卡尔曼滤波算法

·【算法系列】非线性最小二乘求解-直接求解法

·【算法系列】非线性最小二乘求解-梯度下降法

·【算法系列】非线性最小二乘-高斯牛顿法

·【算法系列】非线性最小二乘-列文伯格马夸尔和狗腿算法

文章目录

系列文章

文章目录

前言

一、列文伯格-马夸尔算法

1.LM算法

2.LMF算法

二、狗腿算法

总结

前言

SLAM问题常规的解决思路有两种，一种是基于滤波器的状态估计，围绕着卡尔曼滤波展开；另一种则是基于图论（因子图）的状态估计，将SLAM问题建模为最小二乘问题，而且一般是非线性最小二乘估计去求解。

非线性最小二乘有多种解法，本篇博客介绍列文伯格-马夸尔算法及其变种（狗腿算法）求解最小二乘问题。

非线性最小二乘的一般形式如下：

$\underset{x}{min}\sum \left \| y_{i}-f(x_{i}) \right \|^{2}_{\sum _{i}^{-1}}$

其中 $f(x_{i})$ 是非线性函数， $\sum{_{i}^{-1}}$ 表示协方差矩阵

为了阐述方便，进行如下表示：

$\psi (x)=\sum \left \| y_{i}-f(x_{i}) \right \|^{2}_{\sum^{-1}_{i}}$

一、列文伯格-马夸尔算法

1.LM算法

前面提到GN（高斯-牛顿）算法当展开点距离目标点较远时，可能会出现迭代效果下降，甚至发散的情况，原因是 $J^{T}J$ 不一定正定，而列文伯格和马夸尔两人对GN算法进行了改进，后来Fletcher又对其中的策略进行了改进，即实际中常用的LMF算法。

既然GN算法展开点距离目标点必须保持在一定范围内才有效，那么我们在进行该算法时，可以给迭代更新量 $\bigtriangleup x$ 一个限制范围，以保证GN算法的收敛，那么原来的无约束最小二乘就变成了带约束的最小二乘：

$\bigtriangleup x=\underset{\bigtriangleup x}{argmin}\left \| e(x^{(k)}) + J\cdot \bigtriangleup x \right \|^{2},\left \| \bigtriangleup x \right \| \leq d_{k}$

对于这种问题，在高数中就学过，可以使用拉格朗日乘子 $\mu _{k}$ 将上式转化为无约束的形式：

$\bigtriangleup x=\underset{\bigtriangleup x}{argmin} (\left \| e(x^{(k)}) + J\cdot \bigtriangleup x \right \|^{2} + \mu_{k}\left \| \bigtriangleup x \right \|^{2})$

到这里就和前面一样了，求最小值就对上式求导，使导数等于0，得到下面的线性方程：

$(J^{T}J+\mu_{k}\cdot I)\bigtriangleup x=-J^{T}\cdot e$

LM算法引入了 $\mu_{k}$ 对 $J^{T}J$ 进行了修正，可见LM算法的关键就是选取合适的 $\mu_{k}$ 使得系数矩阵保持正定，这样就可以保证每一步迭代目标函数都会下降。

LM算法是GN算法和梯度下降法的结合产物，当 $\mu_{k}$ 较大时， $\mu_{k}\cdot I$ 占主要地位，忽略 $J^{T}J$ 就变成了梯度下降法；当 $\mu_{k}$ 较小时， $J^{T}J$ 占主要地位，忽略 $\mu_{k}\cdot I$ 就变成了GN算法。

2.LMF算法

既然上面提到了LM算法的关键就是选取合适的 $\mu_{k}$ 使得系数矩阵保持正定，以保证每一步迭代目标函数都会下降，那么我们如何确定 $\mu_{k}$ 的取值呢？

LMF算法给出了依据。

代价函数的变化量为：

$\bigtriangleup \psi =\psi(x^{(k+1)})-\psi(x^{(k)})$

近似函数的变化量为：

$\bigtriangleup \varphi =\varphi(\bigtriangleup x)-\varphi(0)=2\bigtriangleup x^{T}J^{T}e+\bigtriangleup x^{T}J^{T}J\bigtriangleup x$

然后定义一个评价量-线性度 $\gamma _{k}$ 来衡量近似程度， $\gamma _{k}$ 越接近1则证明原函数和近似后的函数变化量越接近，也就是说明展开点的线性度更好。

$\gamma _{k}=\frac{\bigtriangleup \psi}{\bigtriangleup \varphi }$

有了这个评价标准那么LMF算法就简单了，就是根据线性度 $\gamma _{k}$ 的值来确定 $\mu_{k}$ 的取值，当 $\gamma _{k}$ >0.75时（接近1时）说明线性度较好，应用GN算法主导，即 $\mu_{k}$ 应该调小一点（一般减小10倍）；当 $\gamma _{k}$ <0.25时（接近0时）说明线性度较差，应用梯度下降法主导，即 $\mu_{k}$ 应该调大一点（一般增大10倍）；当 $\gamma _{k}$ 在0.25到0.75之间时，认为取值合适，不作调整；当 $\gamma _{k}$ 为负时，说明此时代价函数是上升的，应该拒绝本次迭代更新量，并将 $\mu_{k}$ 调大10倍。

MATLAB实验：

主函数：

% 目标函数为 z=f(x,y)=(x^2+y^2)/2
clear all;
clc;
%构造函数
fun = inline('(x^4+2*y^2)/2','x','y');
dfunx = inline('2*x^3','x','y');
dfuny = inline('2*y','x','y'); 
ddfunx = inline('6*x^2','x','y');
ddfuny = inline('2','x','y'); 

x0 = 2;y0 = 2;                                  %初值

[x,y,n,point] = LMF(fun,dfunx,dfuny,ddfunx,ddfuny,x0,y0);    %LMF算法

figure
x = -2:0.1:4;
y = x;
[x,y] = meshgrid(x,y);
z = (x.^2+y.^2)/2;
surf(x,y,z)    %绘制三维表面图形
% hold on
% plot3(point(:,1),point(:,2),point(:,3),'linewidth',1,'color','black')
hold on
scatter3(point(:,1),point(:,2),point(:,3),'r','*');
n

LMF算法：

%% LMF算法
function [x,y,n,point] = LMF(fun,dfunx,dfuny,ddfunx,ddfuny,x,y)
%输入：fun:函数形式 dfunx(y):梯度（导数）ddfunx(y):海森矩阵（二阶导数） x(y):初值
%输出：x(y):计算出的自变量取值 n:迭代次数 point:迭代点集

%初始化
a = feval(fun,x,y);                                 %初值
n=1;                                                %迭代次数
point(n,:) = [x y a];   
mu=1;                                               %拉格朗日乘子

while (1) 
  
  a = feval(fun,x,y);                               %当前时刻值
  adfun=2*(-(feval(fun,x,y))^0.5/(feval(dfunx,x,y)+mu))*feval(dfunx,x,y)*(feval(fun,x,y))^0.5+((-(feval(fun,x,y))^0.5)/(feval(dfunx,x,y)+mu))^2*(feval(dfunx,x,y))^2;
  x = x - (feval(fun,x,y))^0.5/(feval(dfunx,x,y)+mu);   %下一时刻自变量
  y = y - (feval(fun,x,y))^0.5/(feval(dfunx,x,y)+mu);   %下一时刻自变量
  b = feval(fun,x,y);                               %下一时刻值
  afun=b-a;                                         %原函数增量
  yy=afun/adfun;                                    %线性度
  if(yy>0.75)
      mu=mu/10;
  end
  if((yy<0.25)&&(yy>=0))
      mu=mu*10;
  end
  if(yy<0)
      mu=mu*10;
      continue;
  end
  
  if(b>=a)
      break;
  end
  n = n+1;
  point(n,:) = [x y b]; 
end

实验结果：

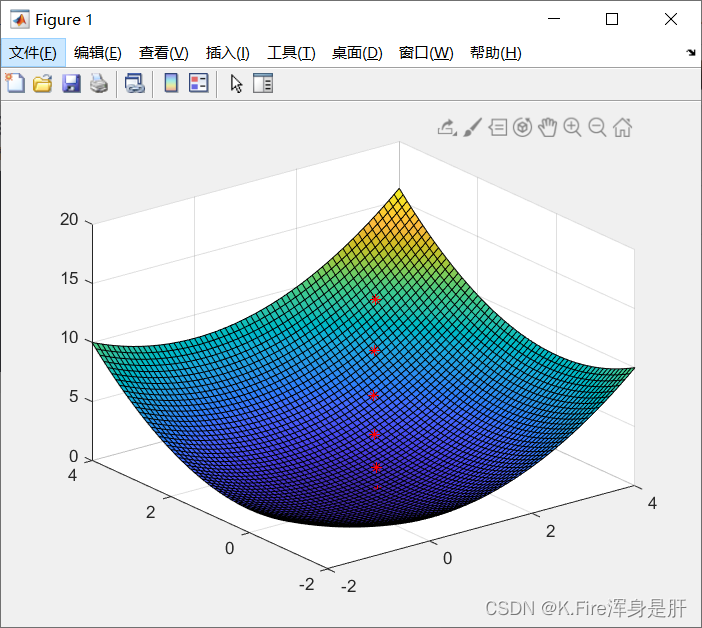
二、狗腿算法

前面的LMF算法已经比较完善，有较好的性能了，但其中仍然存在一点瑕疵，当 $\gamma _{k}$ 为负时，说明此时代价函数是上升的，应该拒绝本次迭代更新量，这就白白浪费了求解这一步的计算代价，Powell提出的狗腿算法就很好的修正了这个问题。

在狗腿算法中，先计算最速下降法的迭代更新量和高斯-牛顿的迭代更新量：

$\bigtriangleup x_{SD}=-\alpha _{k}\cdot 2 \cdot J^{T}\cdot e(x^{(k)})$

$\bigtriangleup x_{GN}=-(J^{T}J)^{-1}\cdot J^{T}e$

在狗腿算法中也是使用线性度来调整参数，但不是调整 $\mu_{k}$ 而是调整 $d_{k}$ （置信域）， $d_{k}$ 与 $\mu_{k}$ 是负相关的，比如线性度好时，说明近似程度高， $\mu_{k}$ 应该调小点使用高斯牛顿算法，相应的 $d_{k}$ 可以调大一点，扩大置信域，具体调整策略如下：

当 $\bigtriangleup x_{GN} \leq d_{k}$ 时，选择高斯牛顿算法，使 $\bigtriangleup x_{DL} =\bigtriangleup x_{GN}$
当 $\bigtriangleup x_{GN}$ 超出置信域时，高斯牛顿算法不一定能让代价函数下降，而最速下降法一定能使代价函数下降， $\bigtriangleup x_{DL}=d_{k}\frac{\bigtriangleup x_{SD}}{\left \| \bigtriangleup x_{SD} \right \|}$ ，取最速下降法的方向，步长取 $d_{k}$ ，因为步长小于 $\bigtriangleup x_{SD}$ 的长度，肯定能让函数下降。
当 $\bigtriangleup x_{GN}$ 超出置信域，而 $\bigtriangleup x_{SD}$ 在置信域内时，就选取二者之间折中的迭代量， $\bigtriangleup x_{DL}=\bigtriangleup x_{SD}+\beta (\bigtriangleup x_{GN}-\bigtriangleup x_{SD})$ ，选取 $\beta$ 使得 $\bigtriangleup x_{DL}=d_{k}$

后面就是根据线性度对 $d_{k}$ 进行调整：

当 $\gamma _{k}>0.75$ 时，说明线性度好，可以将置信域扩大，使 $d_{k+1}=max\{ d_{k},3\cdot \left \| \bigtriangleup x_{DL} \right \| \}$
当 $0.25 \leq \gamma _{k}\leq 0.75$ 时，说明置信域设置合理，不作调整， $d_{k+1}=d_{k}$
当 $\gamma _{k}<0.25$ 时，说明线性度较差，需要将置信域缩小， $d_{k+1}=d_{k}/2$