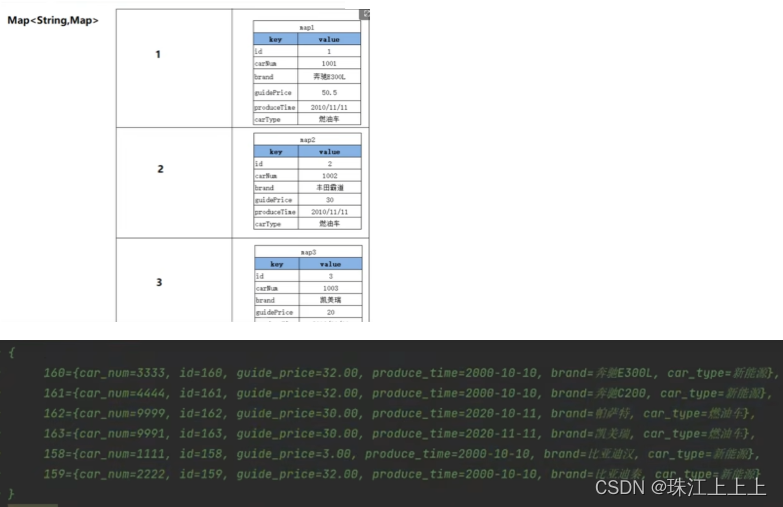
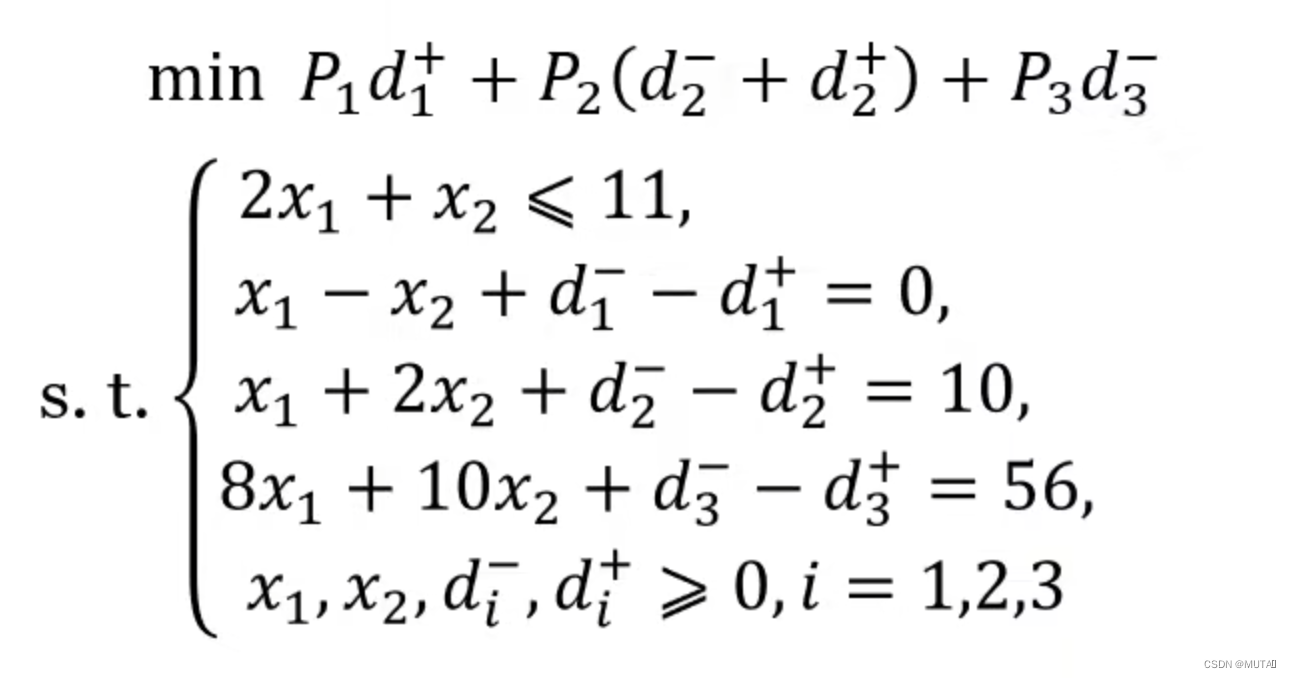动态规划是数学、编程中一个重要的算法

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果

——百度百科

没错你看不懂是正常的，不然我也不需要写这篇文章了（doge）

忘掉刚才的概念

带你重新梳理

一.名字的含义

动态规划

顾名思义，是一种规划问题的策略，还得是动态的

FIRST：怎样的策略呢？

设想一个问题

如果你解决一个问题，在条件允许下，你是不是会尽力给自己争取最大的利益（不考虑人情世故，纯属理性人）

而动态规划，就是给出你的最优解。

最优解有时不是挣最多的钱，拿最多的东西，而要权衡多方面利弊，比如：价值高低、是否重复……

SECOND:动态是什么意思？为什么还得是动态的呢？

在一个解决问题的过程中，大部分情况会有多个步骤

∵ 我们要求得最后的最优解

∴ 每一个步骤也要做到最优解

假设有两个步骤，第一个步骤是最优解，第二个步骤就是最优解中的最优解，也就是我们最后要求的最优解。无论中间哪一个不对，都不能变成最后的最优解

百度百科中这一段说的大概就是这个意思

怎么样？动态规划的意思是不是更明白了（相比较百度百科）

二.动态规划特点

第一个就是刚才说的，最优子结构性质

第二个：无后效性

还是回到我们刚才的栗子（doge

增加成四个步骤

在动态规划中，每个步骤叫做状态

因为我们每一个状态都得是最优解，也就是总结了前面所有的状态，汇集而成的最优解

这就是大名鼎鼎的

无后向性

第三个：子问题的重叠性

这个性质不仅仅在动态规划中出现，在递归中也有

其实这个不能算是特点，更多来说是缺陷吧

插一句题外话

我们教练说，遇到动态规划的题如果不会，可以用递归代替，但拿不到满分

这是为什么呢？

动态规划的优点就在于时间，他已经有效避免了很多重复性的东西

但还是继承了递归的重叠问题

而重叠问题，在实际应用中一定要考虑进去，否则很容易被第二次考虑这个状态时的结果所替代，从而答案错误

看到这里，你是不是对动态规划有了初步的了解？

下一篇文章，我们讲解动态规划怎么在C++中实现

点个赞再走吧