4-1 线性规划_哔哩哔哩_bilibili

4-2 非线性规划_哔哩哔哩_bilibili

4-3 多目标规划_哔哩哔哩_bilibili

1.线性规划

有限条件下，最大收益

1. 例题

例题：张麻子既要攻碉楼又要追替身，他们一伙6人，总共1200发子弹;每有一人攻确楼会给百姓带来40点士气值，每有一人追替身会给百姓带来30点士气值;攻碉楼每人需240发子弹，追替身每人需120发。4问攻碉楼和追替身各派几个人，能使百姓的士气值最大？

---

解：
设派人攻碉楼，排人追替身，百姓士气值为y；

士气值最大:max  

总共6人：;

既要攻碉楼又要追替身：

 子弹有限：则

---

 2. 代码实现

2.1 Linprog函数

模型化为matlab标准型：目标函数最小值、约束条件小于等于号或等号；（如果求最大值，约束条件有大于等于——>求最小值后求反）

•  [x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)
•  x返回最优解的变量取值，fval返回目标函数的最优值；

 

 2.非线性规划

•  线性规划：所有变量都是一次方；
• 非线性规划：至少一个变量不是一次方；

2.1 代码实现

 函数求解：

• [x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
• x得到决策变量取值，fval得到最优解取值

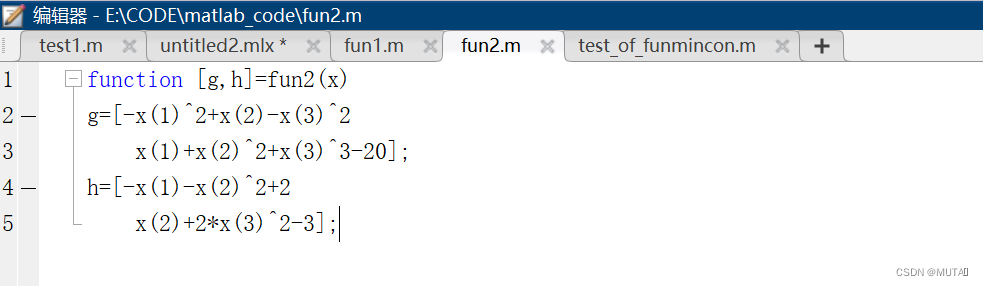
本题：设好后fun和nonlcon函数文件以及其他参数后，执行：

[x,y]=fmincon('fun1',[0;0;0],[],[],[],[],[0;0;0],[],'fun2')

 

 3.多目标规划

3.1 例题

 

3.2 概念

需要衡量每个目标的完成情况，并主观上区分三个目标的重要性,使得整体的完成情况尽量好
引入三个概念:正负偏差，绝对约束和目标约束,优先因子

3.2.1  绝对约束和目标约束

• 绝对约束是模型中自带的约束条件，必须满足，否则是不可行解
• 例如，使用材料的数量不能超过总共数量

3.2.2 目标约束

• 目标约束是模型中对不等式右端追求的值允许有偏差
• 目标3:尽可能使利润不少于56万，也就是，但允许有偏差
• 这个“偏差”就是加入正负偏差变量，变成:

 3.2.3 优先因子

1.尽量使产品I的产量不超过产品II的产量; 2.尽可能充分利用所有设备; 3.尽可能使利润不少于56万
这三者到底哪个重要?需要主观上确定优先因子。
例如，我认为目标3最重要，给他优先因子是10;目标2第二重要，给他优先因子5; 目标1第三重要，给它优先因子是1。那么三个目标重要性之比是10: 5: 1
 

第一目标要求不超过目标值，一位置正偏差变量越小越好

 3.3 解题

需要衡量每个目标的完成情况，并主观上区分三个目标的重要性，使得整体的完成情况尽量好

• 把所有的目标约束都加上变成灯饰（注意，绝对约束也可以这样做变成等式，视情况而定）
• 按照需求，主观确定确定优先因子

 得到多目标规划模型：

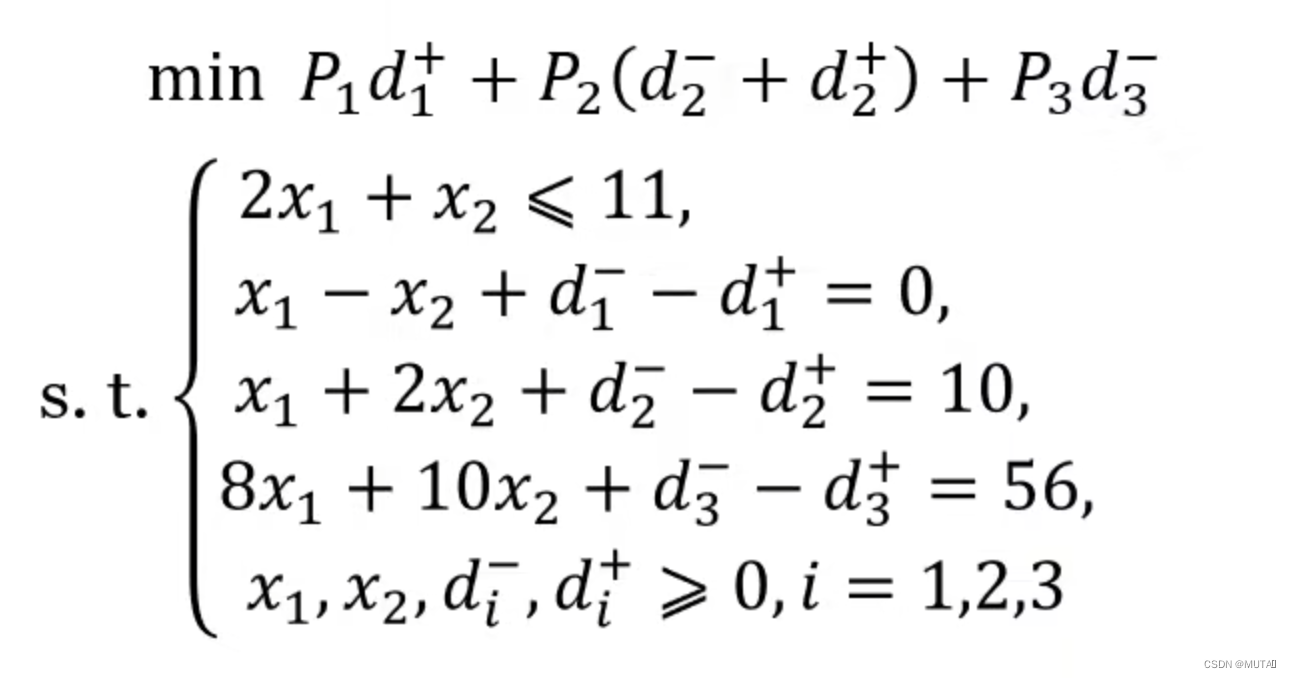
 求解方法：fgoalattain函数；或序贯算法；或用Lingo求解