机器学习
- 一、机器学习常见算法(未完待续...)
- 1.算法一:线性回归算法:找一条完美的直线,完美拟合所有的点,使得直线与点的误差最小
- 2.算法二:逻辑回归分类算法
- 3.算法三:贝叶斯分类算法
- 4.算法四:KNN分类算法
- 5.算法五:KMeans算法
- 巨人的肩膀
一、机器学习常见算法(未完待续…)
1.算法一:线性回归算法:找一条完美的直线,完美拟合所有的点,使得直线与点的误差最小
- 干货前的杂谈
- 之前学的Hadoop生态中的东西们,都是为了应对海量(历史)数据的存储与计算。而真正的展望未来是基于历史数据对未来进行预测。
- 科普:
- 国外,亚马逊的推荐系统质量比较高是因为亚马逊掌握的数据质量高。
- 另外,
5G时代到来后形成万物互联,就像一个八爪鱼,5G这个词(基建)位于中心,每个爪爪有着自己独一枝的终端设备。此时,如果每个终端设备需要处理数据等业务时必须得和中间的5G中心交互,这时间成本太高,所以“引入边缘计算”。临近的终端设备可以互相帮忙。但是互帮互助也不能让邻居白帮忙呀,所以得引入“区块链”进行记账、付费等。
- 数据+算法==>模型(规律)
- 数据量决定了模型的高度,算法只是逼近这个高度
- 线性回归算法整体思路:

- 1.随机产生w参数
- 其实就是不断调整完美直线的指向与坐标轴的交点,找到误差值最小的w参数,也就相当于找到了完美直线
- 2.把w参数与样本数据带入到误差函数中求解误差值
- 3.误差值与用户指定的误差阈值比较
- 如果大于用户指定的误差阈值,继续调整w参数
- 如果小于用户指定的误差阈值,那么此时的w参数就是最佳的w参数
- 1.随机产生w参数
- 线性回归具体知识点
- y=w0 + w1 * x;此时咱们需要两组数据才能确定这个方程,因为(有两个未知数)两点确定一条直线(多一个点少一个点都不行)。具体到咱们机器学习、大数据这块,咱们有好几亿组数据,我们此时
需要找到一根离好几亿数据最近的且能代表数据规律的完美直线【这个规律不就是w参数嘛】- 当咱们x不止一个时,就要找的是多元线性回归:y=W0+W1X1+W2X2+…+WnXn
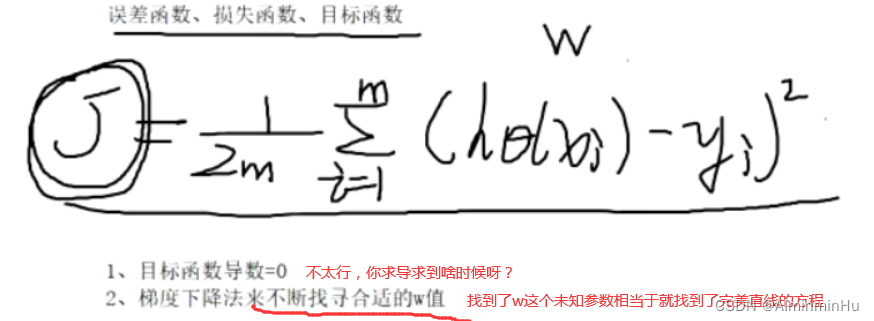
- 线性回归算法的量化公式:

- 当咱们J(θ)值越小,证明咱们好几亿数据跟直线的误差越小,不就相当于说咱们已经找到这条完美直线【这条完美直线指的是这条直线到所有点的距离最小,也就是所有点的误差最小】了嘛
- 这个J(θ)叫做误差函数/损失函数/目标函数
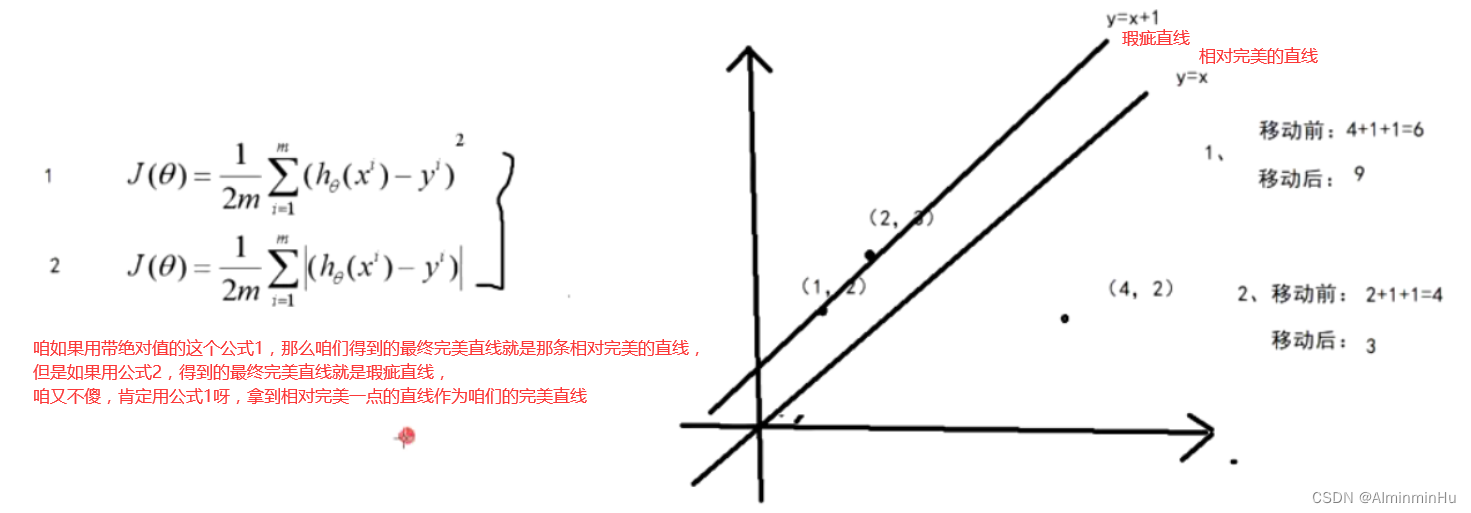
- 损失函数为什么用平方而不是绝对值【平方,当误差比较大时会放大误差,从而会在全局的角度中帮咱们找到更好的完美直线】
- 完美直线如果是曲线,虽然说曲线能够拟合所有的点也就是说能够保证误差很小,但是曲线不能体现出数据的规律,所以曲线算作过拟合,而不是完美直线体现出来的完美拟合
- 过拟合问题如何控制:把好几亿数据这个数据集分(代码中可以用data.RandomSplit方法来分)为三块【从原始好几亿数据中随机选取出来的数据分为三块】:验证集、训练集、测试集
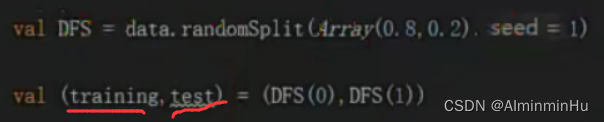
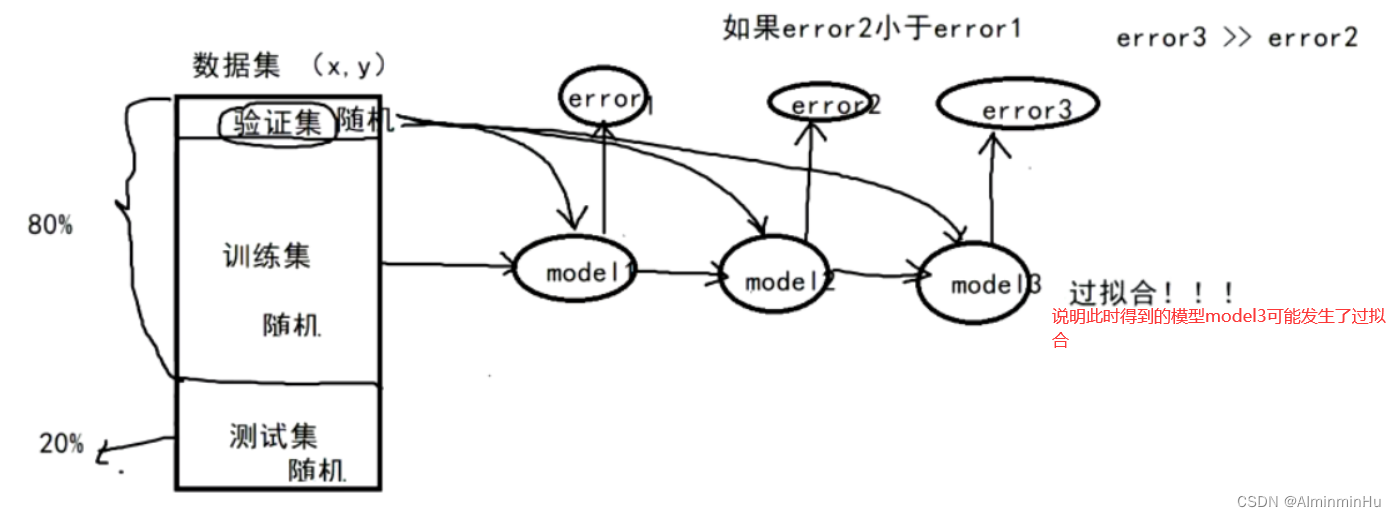
- 验证集:不参与训练模型的,可以用验证集来防止过拟合。验证集的目的是辅助训练模型
- 测试集:测试model2,参与训练模型过程
- 过拟合问题如何控制:把好几亿数据这个数据集分(代码中可以用data.RandomSplit方法来分)为三块【从原始好几亿数据中随机选取出来的数据分为三块】:验证集、训练集、测试集
- 当咱们J(θ)值越小,证明咱们好几亿数据跟直线的误差越小,不就相当于说咱们已经找到这条完美直线【这条完美直线指的是这条直线到所有点的距离最小,也就是所有点的误差最小】了嘛
- 咱们的目标是这个J(θ)值越小越好【这个J(θ)是个凹函数,所以这个J(θ)有极小值】,所以可以通过求导(求偏导)然后令导数为0求出未知数。但是在海量数据下,通过求导令导为0求极值根本不太现实,你求导求到啥时候。所以此时通过正向试参数这种方法,其实就是**
令参未知数为0为1...同时和几亿个数据或者叫点带入到误差函数中,求出一个J(θ)误差值,如果这个误差值在咱们可接受的范围内,不就相当于把未知参数试出来了嘛【其实咱们试w这未知参数就是在改变直线的方向和与坐标轴的交点,从而确定在w这未知参数为多少时直线与点的距离最近,也就相当于误差最小】**。未知参数有了相当于直线的方程不就有了,不就相当于找到完美直线了嘛。

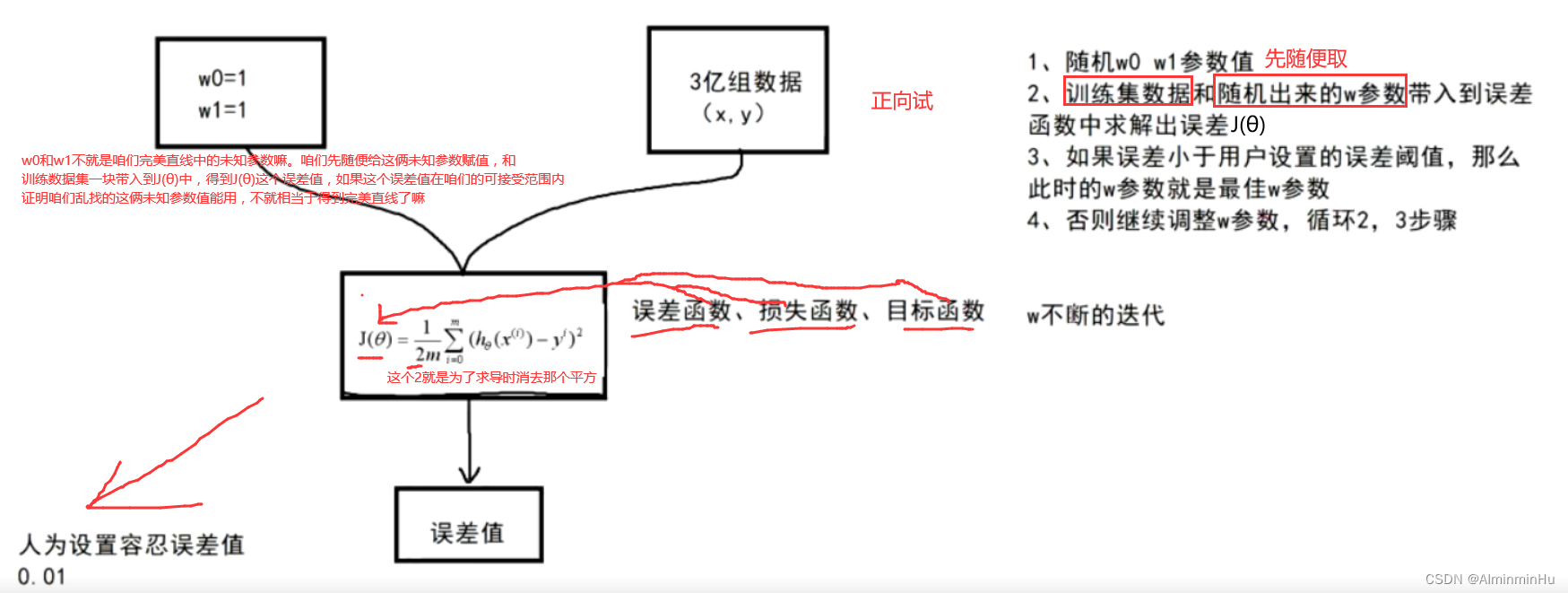
- 然后咱们得到y=w0 + w1*…x…,不就可以把x带入到完美直线中,此时得到的y值就是预测值
- 你量化公式如果不加平方,误差之间可能会抵消,这不是耽误事呢嘛,所以得加平方
- 此时咱们目标是想预测的y值准确些,所以咱们此时玩的是y轴方向上的误差。或者说此时的点到直线上的距离是y轴方向的并不是真正的点到直线的距离【真正的点到直线的距离是要做垂线的哦】
- 但是J(θ)并不是越小越好,可能会出现过拟合等情况
- 光说试w这未知参数,那咋调呢,就是
梯度下降法【梯度下降法指的就是调整w参数这种方法,用来优化损失函数,梯度的方向总是指向函数增大的方向,而咱们w参数调整的方向正好是梯度相反的方向,所以叫做梯度下降法】
- 然后咱们得到y=w0 + w1*…x…,不就可以把x带入到完美直线中,此时得到的y值就是预测值
- 梯度下降法


- 如果导数<0,w参数往大了调整;【
导数的正负决定了w参数的调整方向,公式中的α决定了每次w调整的步长【步长α不能太大,步子迈的太大会让误差变大的,这跟咱们的期望不是反着来了嘛】【但是α太小速度又很慢,所以α不能太小也不能太大】,α一般取0.2、0.3左右】- 往大了调整相当于w参数加上一个东西,也相当于w参数减上导数(因为导数此时为负数呀,负负得正,不就相当于w参数加上了什么东西)
- 如果导数>0,w参数往小了调整;
- 往小了调整相当于w参数减上一个东西,此时咱们就用w参数减上导数(因为导数此时为正数呀)。这样一来正好能跟导数<0那种情况合并起来
- 如果导数<0,w参数往大了调整;【
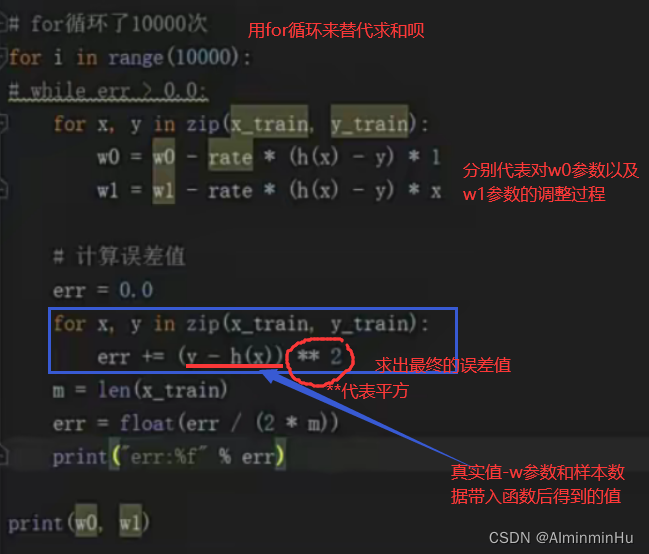
- 在训练模型的时候,一般都会指定收敛条件【多个收敛条件,满足一个即可停止迭代】,不然会无休止的调整参数,
一般常用的收敛条件有两个:- 1.迭代次数:在代码中可以用for i in range(10000):,相当于指定迭代次数为10000.迭代了10000次
- 2.误差容忍度0.01:在代码中就是while err > 0.00001:,指定误差容忍度或者说用户指定的误差阈值
import numpy as np ... def h(x): #定义一个函数h(x) return w0 + w1 * x #函数h(x)的返回值 # Spark mllib是一个机器学习库,封装好了咱们经常用的机器学习算法,可以跟Anaconda一块使用
- 线性回归的抗噪声以及抗冗余
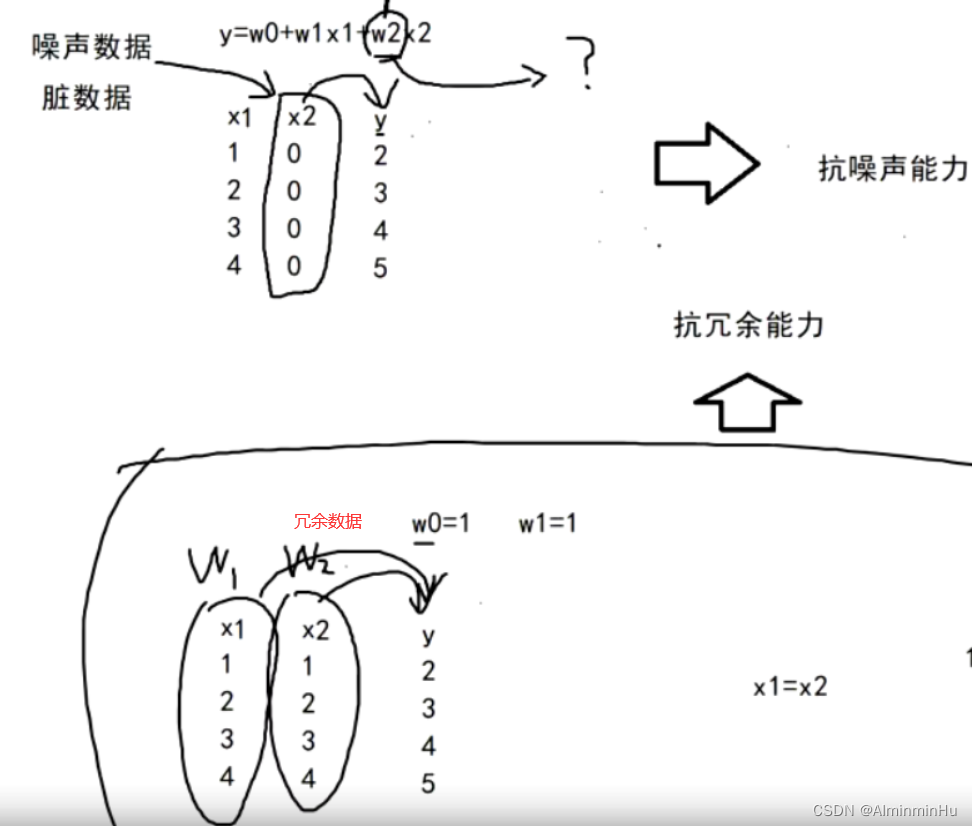
- y=w0 + w1 * x;此时咱们需要两组数据才能确定这个方程,因为(有两个未知数)两点确定一条直线(多一个点少一个点都不行)。具体到咱们机器学习、大数据这块,咱们有好几亿组数据,我们此时
2.算法二:逻辑回归分类算法
- 逻辑回归又叫logistic回归,是一种广义的线性回归【逻辑回归底层也算是用的是线性回归或者说多元的线性回归】分析模型,逻辑回归也算是一种用于分类的算法

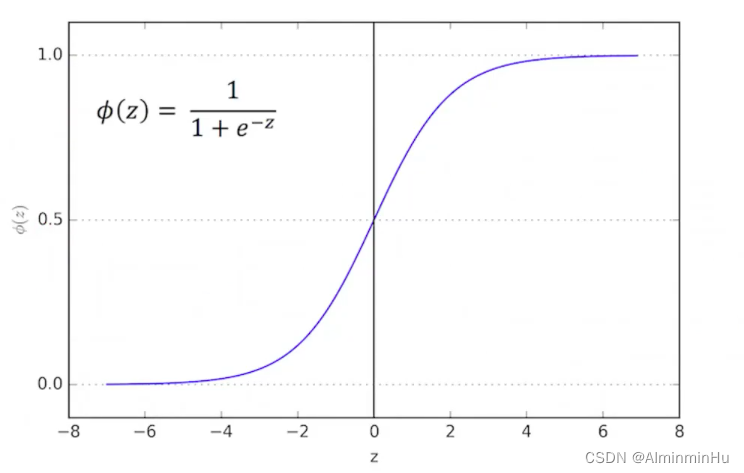
- 咱们用Y=0.5作为咱们人为设置的一个阈值【
分类阈值可以调整,判断日常消费这种0.51、0.49就可以得到结论推送结论了。但是诊断病情、股票这些高精尖的0.9左右你才敢得结论推送结论吧】,不就可以进行分类了嘛【计算出来的y值大于0.5属于上面那一类,小于0.5属于下面那一类】- Z无限大则Y值无限逼近于0,Y越逼近1越属于上面那一类
- Z无限小则Y值无限逼近于1,从图像也可以看出来呀
- 样本倾斜:
- 训练集数据发生了严重的数据倾斜,会导致结果有误差或者有错
- 解决训练集数据倾斜的方法:调整两类数据的权重为一样的
- 上采样:少的多复制几份
- 下采样:从多的那部分中抽取一部分,和少的保持一致
如果空间中样本的分布如下,那么无法准确找到一根分类线来将数据分开【一根直线无法分开样本数据,有可能就表示咱们需要升高维度喽】,此时就要调整样本的维度或者换个非线性算法
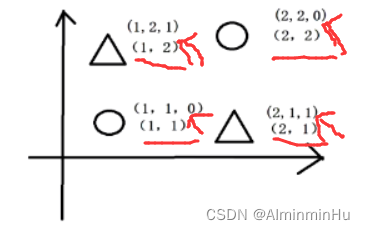
- 将样本数据的维度升高,2->3,高维的数据一定是基于已有的两维数据经过一系列计算得来的【不断的试】
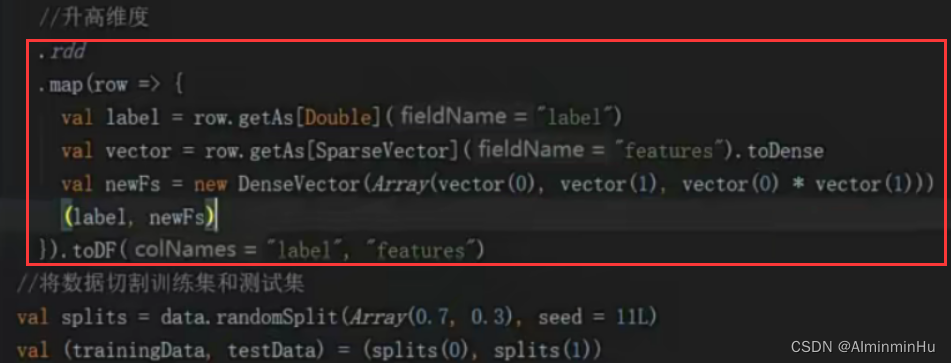
- 将样本数据的维度升高,2->3,高维的数据一定是基于已有的两维数据经过一系列计算得来的【不断的试】
- 模型正确率是50%证明模型很差,这跟咱们瞎猜差不多
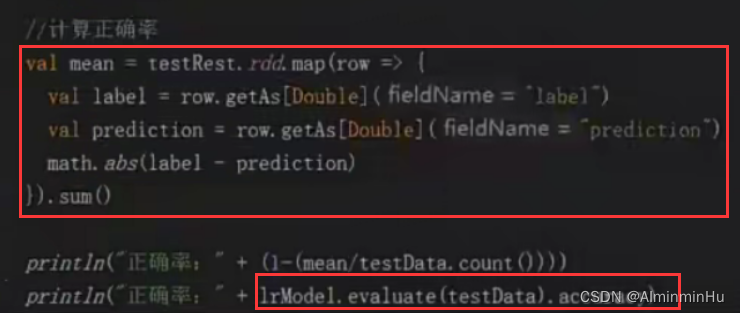
- 假如训练逻辑回归算法模型时要求分类的直线过原点,也就是无截距
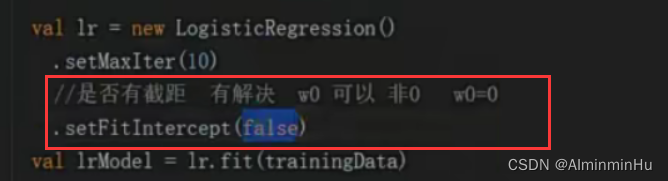
- 这就是难题了,平时咱们的都有截距,有截距一般能够很好的对样本数据进行分类
- 逻辑回归的误差函数/损失函数
下面的误差函数针对计算一条样本的误差【咱们最终分类的目的就是得出y到底属于哪一类呀,所以y就是代表当前样本的真实分类号】
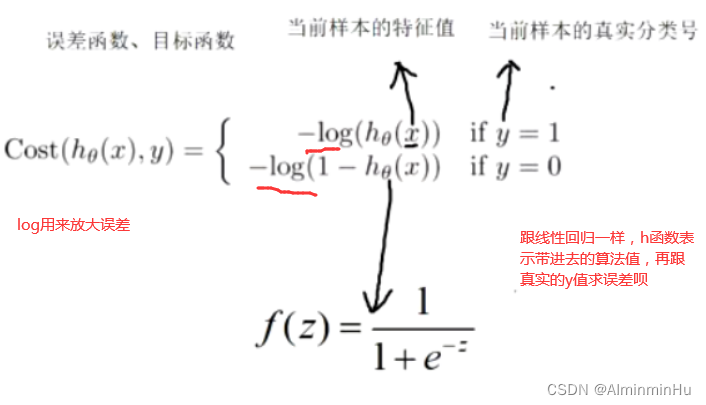
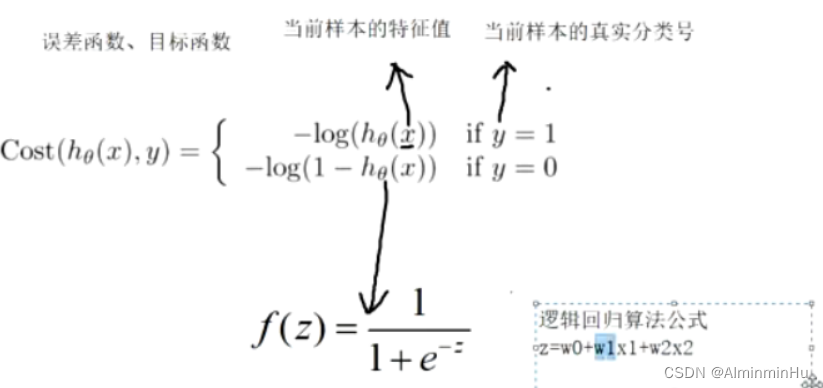
- 就算多条样本的误差函数/目标函数:

- 咱们还是利用梯度下降法来优化目标函数或者说误差函数
梯度下降就是通过对目标函数或者叫误差函数求导,根据导数来决定w参数的调整方向,利用结合步长α和导数一块优化误差函数或者说目标函数
逻辑回归算法训练模型的整体流程:- 1.随机产生w参数值
- 2.将我们的训练集数据和w参数带入到误差函数中计算出误差
- 3.将误差与用户指定的误差预知相比较
- 计算出来的误差值小于用户指定的误差阈值,则对应的w参数就是最佳的w,相当于w参数对应的分割线就是最佳的分割线
- 计算出来的误差值大于用户指定的误差阈值,说明还需要调整,那就继续对误差函数求导,依据导数的大小来确定w参数的调整方向,同时使用用户指定的α来调整w参数,如果计算出来的误差依然大于用户指定的误差阈值,则迭代2,3步骤,直到误差小于用户指定的误差阈值
- 逻辑回归常用优化方法:
- 归一化:训练集中各个特征数量级差得很大,调整w参数时可能数量级差距很大,造成错误,所以要进行归一化
- 对数据做归一化,将数据映射到0-1之间
- 归一化方法
- 最大最小值归一化:((特征值-min)/(max-min))。最大最小归一化缺点是容易受到离群值的影响
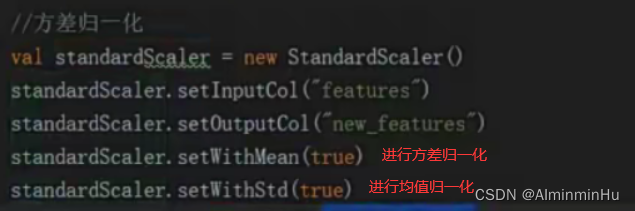
- 方差归一化
- 优点:抗干扰能力强,和所有数据都有关,求方差需要所有值的介入,若有离群值的话,离群值的影响会被方差归一化抑制下来
- 缺点:最终未必会落到0到1之间
- 归一化后还有问题:
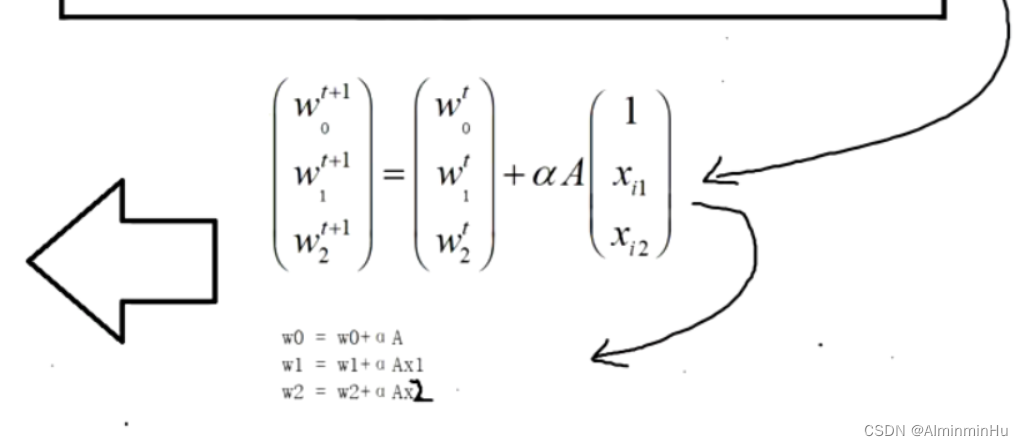
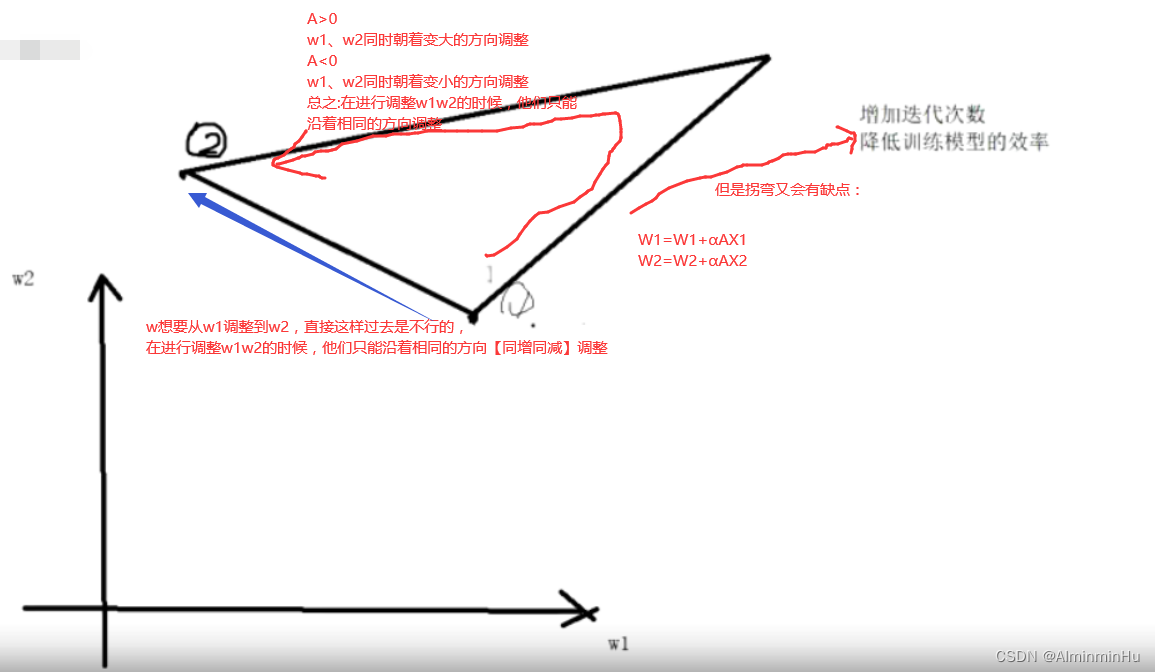
- 所以,总的来说,还是拐弯效率高,那怎么样能够实现拐弯呢。
进行均值归一化,让每个数量减去平均数,让w1和w2有正有负,就可以实现拐弯去调w参数
- 所以,总的来说,还是拐弯效率高,那怎么样能够实现拐弯呢。
- w越大的优点和缺点:同理,w越小正好对应w越大的缺点和优点,所以w并不是越大越好或者越小越好,而是刚刚好才好
- 优点:

- 缺点,会放大噪声数据【w越大越会受噪声的影响,抗干扰能力越小】
- 优点:
- L1正则化与L2正则化:为了达到刚刚好的w参数这个目的,需要重写一些误差函数,在原来的误差函数后面加了一项带有惩罚系数(λ)的正则化项
- 通过L1正则化把w调的刚刚好【前一部分一大坨求和用来保证模型的正确率,后一部分λL用来保证抗干扰能力 】
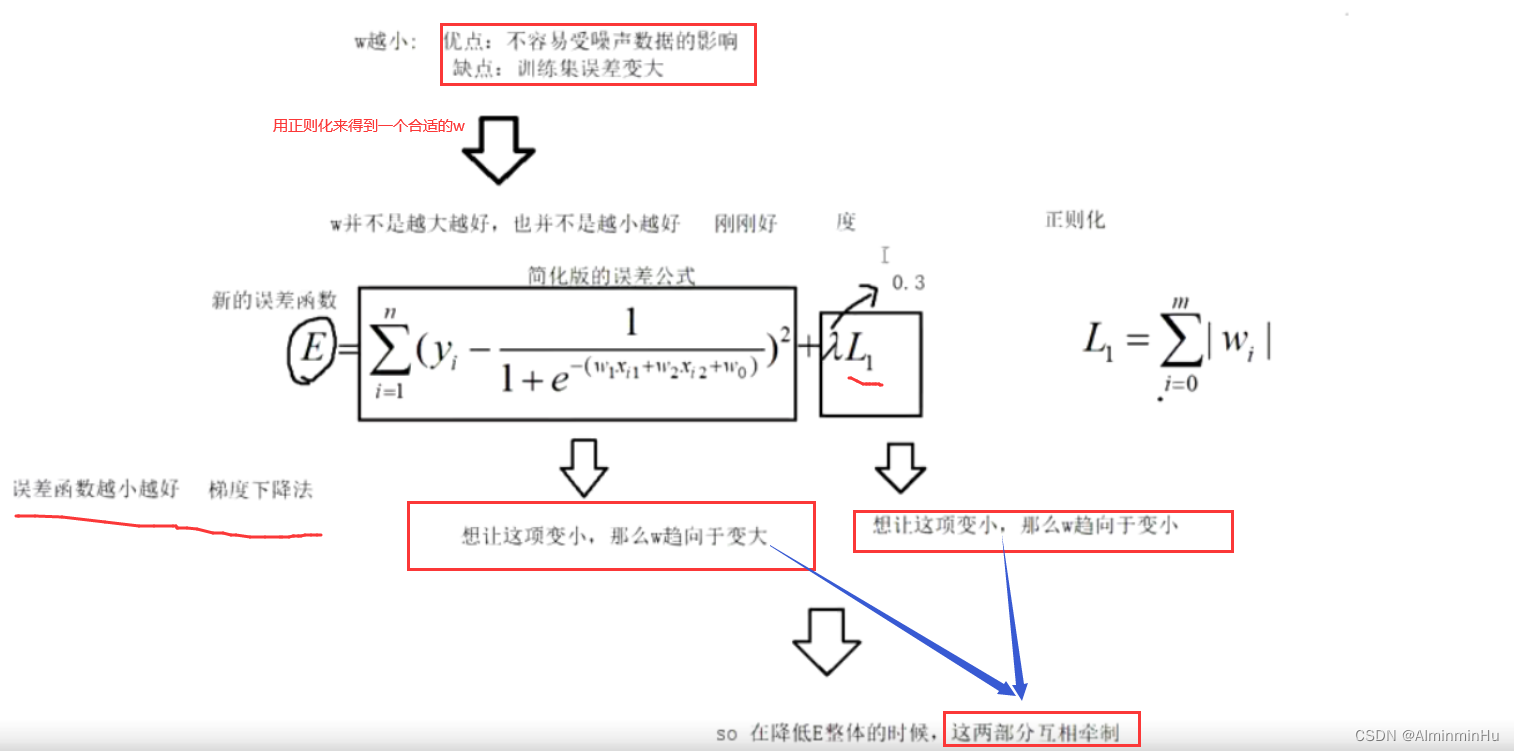
- 如果这个λ=0.3,说明咱们更看重前面那一坨简化版的误差公式
- 如果这个λ=1,说明同时看重简化版的误差公式以及带有惩罚系数的正则化项
- L2正则化:
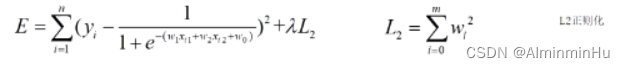
- L1正则化与L2正则化区别:L1正则化是把w参数取绝对值再累加起来,L2正则化是把w参数求平方再累加起来

- L1正则化使得w参数趋向于0
- 同时L1还可以降维,体现出矩阵中为0的w参数,w=0没用呀,所以比如六个w参数相当于六维,咱们就可以去掉那些0,不就相当于降维了嘛
- L2正则化使得w参数趋向于整体变小
- L1正则化使得w参数趋向于0
- 通过L1正则化把w调的刚刚好【前一部分一大坨求和用来保证模型的正确率,后一部分λL用来保证抗干扰能力 】
- 归一化:训练集中各个特征数量级差得很大,调整w参数时可能数量级差距很大,造成错误,所以要进行归一化
- 咱们用Y=0.5作为咱们人为设置的一个阈值【
- 常见的分类问题:根据输入的特征数据来获取因变量y从而判断出分类结果
- 判断是…或者不是…,吃饭没吃饭、生病没生病、吃药没吃药…
- 股票预测
- 确诊及未确诊
- 价格预测涨跌
- 逻辑回归算法和线性回归算法的比较
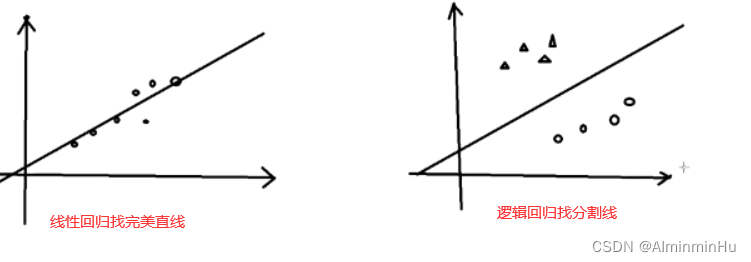
- 线性回归算法简单回忆:
- 线性回归算法简单回忆:
- 逻辑回归实际项目部分点总结
- 逻辑回归算法实现交通路况预测:
所有的多分类都可以归结为二分类,本类+其他类不就相当于二分类了嘛,我管你其他类是多少类呢- 路况四种类型:A类(严重拥堵)、B类(拥挤)、C类( 缓行)、D类(畅通)。【路况类别粒度越细,抗干扰能力越强】
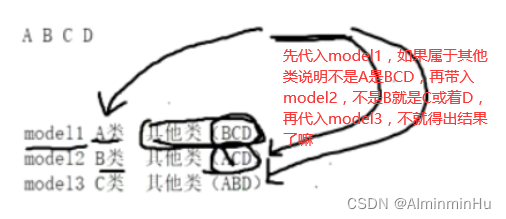

- 模型model1:A类、其他类(BCD)
- 模型model2:B类、其他类(ACD)
- 模型model3:C类、其他类(ABD)
- 路况四种类型:A类(严重拥堵)、B类(拥挤)、C类( 缓行)、D类(畅通)。【路况类别粒度越细,抗干扰能力越强】
整体思路:用指定路段的历史拥堵情况来预测未来路况,先实现实时路况数据统计【数据源源不断写入后台的MQ中,将数据放入redis中,然后用SparkStreaming去进行实时处理】,然后用统计而来的历史数据先进行模型的训练,然后进行交通路况的预测。- 统计卡口的数据:卡口数据形式:卡口号、车牌号、车辆经过卡口的时间、车辆经过卡口的速度
经过卡口的速度需要用一段时间内(比如说五分钟内)的经过这个卡口所有车辆的速度除以车辆总数量就能得到这个卡口所在路段的平均速度衡量【用历史数据衡量这一刻的速度,来排除偶然因素的影响】。在SparkStreaming中有个窗口函数是reduceByKeyAndWindow(5min, 10min) #窗口长度为5,10代表每隔10min计算一次
- 统计卡口的数据:卡口数据形式:卡口号、车牌号、车辆经过卡口的时间、车辆经过卡口的速度
- 编程思路:
你的训练集是什么样的,训练出来的模型就具备什么样的功能(规律)- 实时统计路况拥堵状况,利用流式计算框架SparkStreaming,每条路每分钟的拥堵情况都计算出来,然后把数据存到redis中
- 1.将卡口数据写入kafka
- 写数据直接向kafka中写,而消费者拿数据消费是从zookeeper集群中节点中拿【因为zookeeper中记录着用户数据的偏移量】
- 2.用SparkStreaming去消费kafka中数据
- 1.将卡口数据写入kafka
- 构建训练集:训练集存到redis中,但是redis是基于内存的,所以给HDFS中也存一份
- 利用redis中的数据进行预测
- 每一条路对应一个模型model。假设为通过最近三分钟的数据预测接下来一分钟的路况
- 影响A中路的要素有两方面。【当然啦,实际影响因素有很多,天气、周六周日等…】

- 影响A中路的要素有两方面。【当然啦,实际影响因素有很多,天气、周六周日等…】
- 假设通过最近三分钟的数据来预测第10分钟后的路况(拥堵程度)

- 欲训练模型的卡口号对应路段,及其影响要素
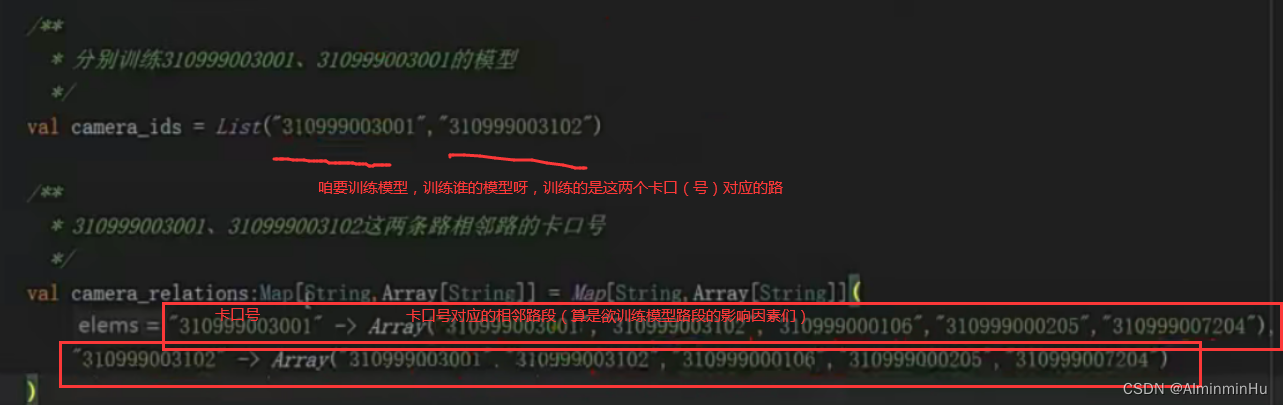
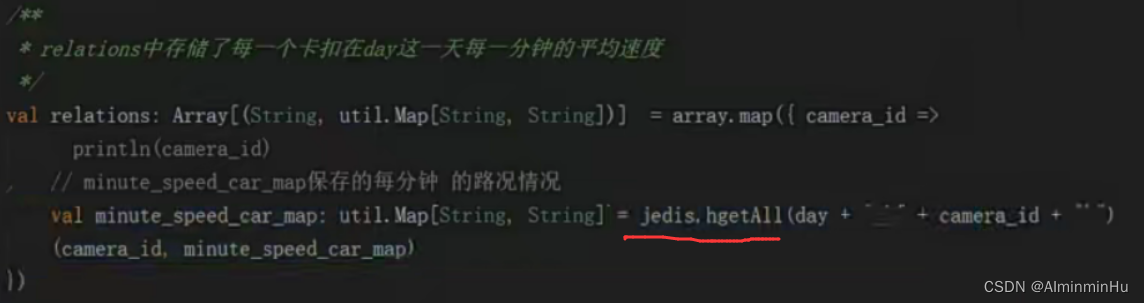
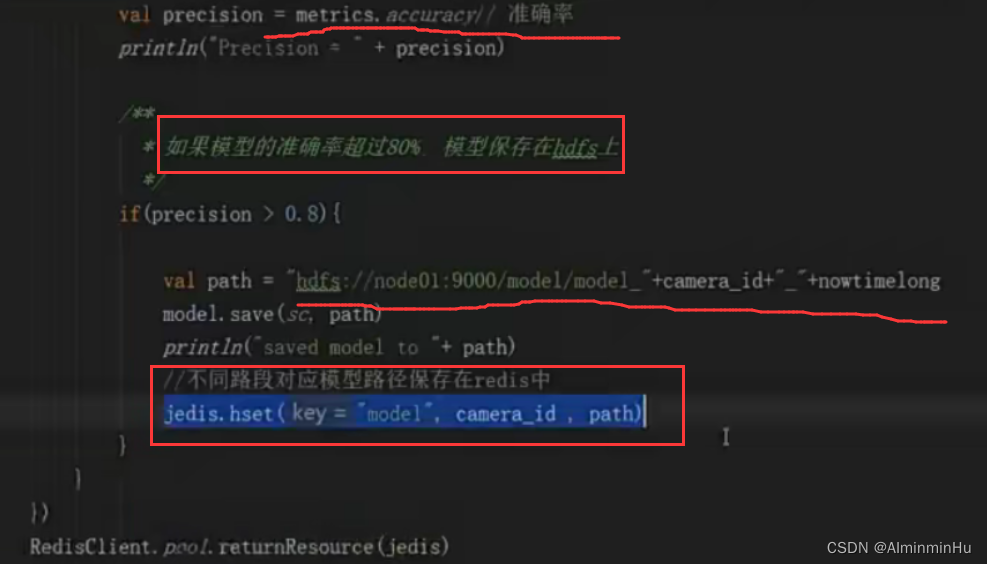
- 如果模型的准确率超过80%,则模型保存在hdfs上
- 欲训练模型的卡口号对应路段,及其影响要素
- 假设通过最近10分钟的数据,来预测第5分钟的拥堵情况

- 每一条路对应一个模型model。假设为通过最近三分钟的数据预测接下来一分钟的路况
- 实时统计路况拥堵状况,利用流式计算框架SparkStreaming,每条路每分钟的拥堵情况都计算出来,然后把数据存到redis中
- 逻辑回归算法实现交通路况预测:
3.算法三:贝叶斯分类算法
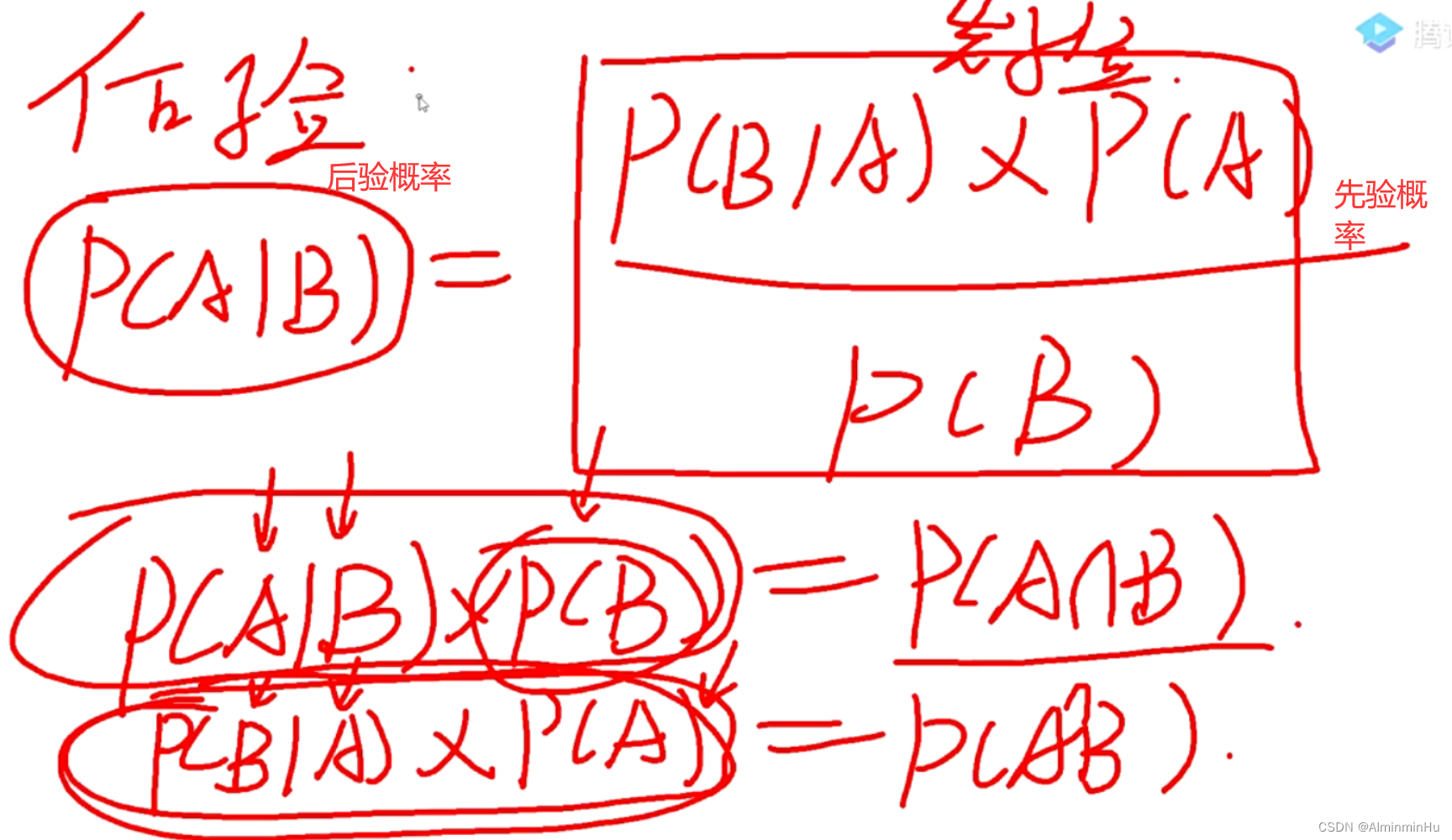
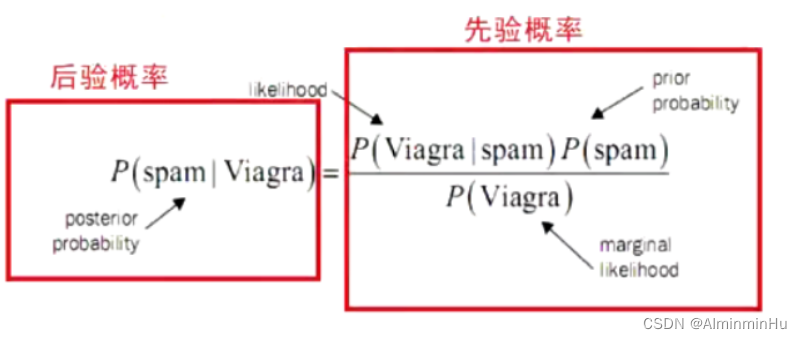
- 来源于一篇逆概文章。【正向概率问题指的是顺着推导就能推导出来的那种】
- 训练贝叶斯算法模型,就是在统计概率得到概率表,然后依据表预测未来
- 常用于,比如邮件分类,垃圾邮件及非垃圾邮件。
- 做法就是整理思路,得到概率表
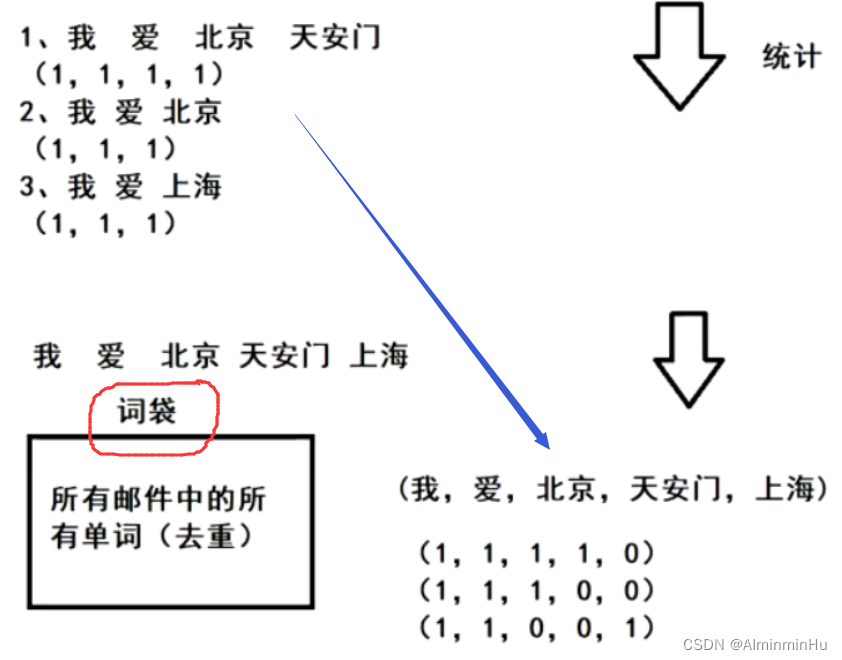
- 当基数太小时,贝叶斯可能会不符合客观事实,所以可以用拉普拉斯平滑定理【给分子分母都加上一个数,让最终概率符合客观事实】
- 做法就是整理思路,得到概率表
4.算法四:KNN分类算法
- 所谓的识别数字/字母,其实就是一个分类过程【需要有对应的数字或者字母的数据,数据是什么样的,训练出来的模型就具备什么样的功能】。常见的场景有web识别车牌号码、数字、验证码
5.算法五:KMeans算法
- 根据两个样本之间的距离,来对样本数据进行划分堆,咱们也得确定聚类,要聚的是哪几类
- 实现KMeans算法。【
可以自己实现,也可以用python中的scikit-learn机器学习库(封装了大量的机器学习算法),来做KMeans聚类】- 1.随机产生K个中心点(中心点可以是真是存在的,也可以是虚拟的)
K的值是咱们不断试出来的,得到一个合适的K值【这个合适的K值可以使得聚类效果很好,也就是类内部相似性很高,类之间差异很大】。咱们K值就可以用matplotlab画出图来看一下,看看聚成的几个类在K为何值图中分的类合适
- 2.计算空间中到K个中心点的距离
- 距离指的是欧氏距离等
- 3.看一下空间中的样本距离哪一个中心点最近
- 4.归完类之后,我们要重新计算K个类的新的中心点(这个类所有样本的横纵坐标取均值)
- 5.计算空间中的样本与新的K个中心点距离
- 6.归类
- 7.直到新的中心的坐标与上一次中心点的坐标不再发生变化
- 1.随机产生K个中心点(中心点可以是真是存在的,也可以是虚拟的)
- KMeans算法在推荐系统中的应用
- 推荐系统:根据用户的兴趣爱好去推荐用户感兴趣的信息或者商品、抖音、快手、电商领域的京东、天猫、亚马逊。推荐系统产生的本质就是信息过载(信息量过大)。
- 但是信息总会有错,有丢失,你咋也不可能100%把所需要的数据都搞到手,方方面面的,所以得靠技术手段,也就是机器学习算法、KMeans解决字段丢失问题,然后数据齐全之后,可以利用“基于用户的协同过滤”或者“基于物品的系统过滤【物品捆绑买卖次数,有时候上架新商品,没有捆绑经历,所以得通过一些手段搞出来捆绑记录】”等推荐算法再结合其他的算法去实现推荐。
- 协同意思是协同别人的数据,看看自己的有别人的数据的相似性,进而去给你推荐
- 但是信息总会有错,有丢失,你咋也不可能100%把所需要的数据都搞到手,方方面面的,所以得靠技术手段,也就是机器学习算法、KMeans解决字段丢失问题,然后数据齐全之后,可以利用“基于用户的协同过滤”或者“基于物品的系统过滤【物品捆绑买卖次数,有时候上架新商品,没有捆绑经历,所以得通过一些手段搞出来捆绑记录】”等推荐算法再结合其他的算法去实现推荐。
- one-hot编码:搞一个库,然后把每种组合以矩阵的形式展示或者说统计出来

- 推荐系统:根据用户的兴趣爱好去推荐用户感兴趣的信息或者商品、抖音、快手、电商领域的京东、天猫、亚马逊。推荐系统产生的本质就是信息过载(信息量过大)。
巨人的肩膀
马士兵老师B站的课
吴恩达老师B站的课
舍友给的资料
XXX权威指南




![[面试八股] Mysql](https://img-blog.csdnimg.cn/d62552615bbd4602920d319e5e95e80c.png)