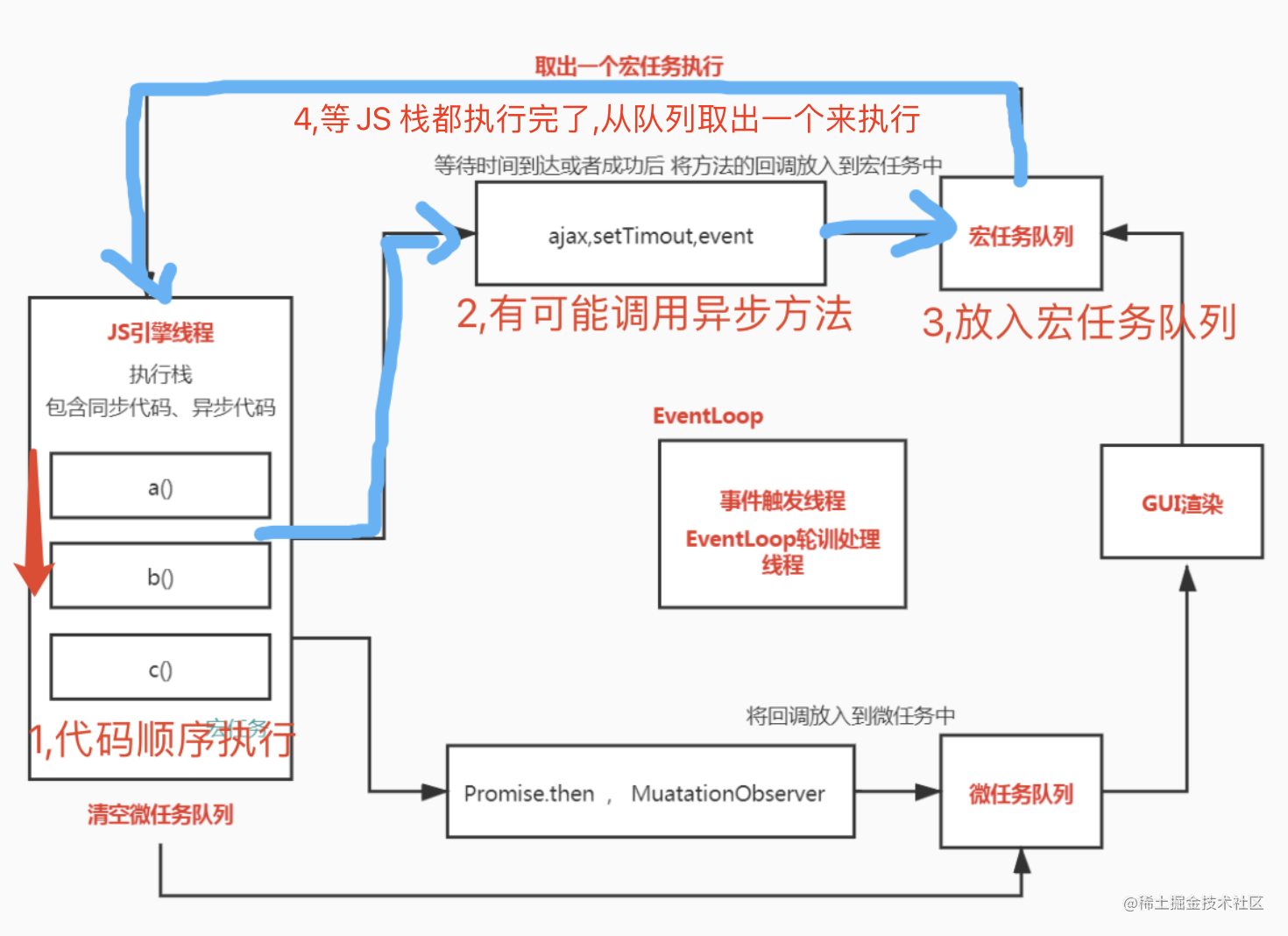
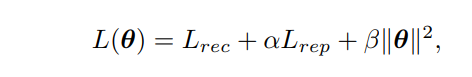介绍
- 主页 https://nv-tlabs.github.io/DMTet/
- 论文pdf https://nv-tlabs.github.io/DMTet/assets/dmtet.pdf
- 视频汇报 https://slideslive.com/38967642/deep-marching-tetrahedra-a-hybrid-representation-for-highresolution-3d-shape-synthesis?ref=homepage
- 疑似代码 在nvdiffrec项目下的工具代码
- 用DMTet恢复点云 https://github.com/NVIDIAGameWorks/kaolin/blob/master/examples/tutorial/dmtet_tutorial.ipynb
- 列表包含两个DMTet的demo https://kaolin.readthedocs.io/en/latest/notes/tutorial_index.html
DMTet的全称为Deep Marching Tetrahedra,是MT(Marching Tetrahedra)算法的深度学习版本。顾名思义,它与MT算法有共通之处,而它又是基于深度学习(Deep)的方法。整个论文的各个步骤都是端到端的、可微的,因而可以被反向梯度重传所训练。
从概览图可知,输入可以使点云或者粗voxel,算法会先细分生成隐式表达SDF,再用MT算法生成显式表达,最后得到模型参数表面(Parametric Surfaces)。
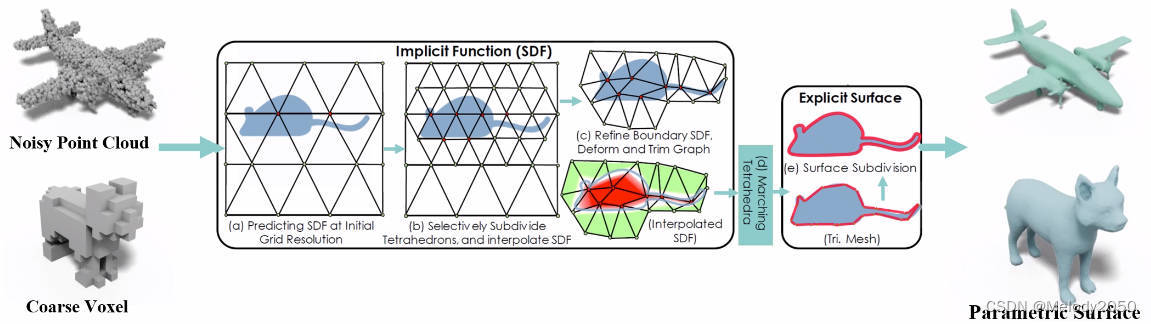
利用崭新的混合3D表达方式,DMTet能集合隐式和显式的3D表达。
- 当前的隐式表达方法的做法,大多是被训练来拟合signed distance values。相比于它们,本论文直接优化重建的表面,从而能够用更少的物体来合成更细微的几何细节
- 当前的显式表达方法的做法,大多是3D深度生成模型,直接生成显式表达,比如mesh。本论文能够合成有任意拓扑的物体形状。
相关概念
chamfer distance
https://www.cnblogs.com/ariel-dreamland/p/13225299.html
3D点云中的倒角距离
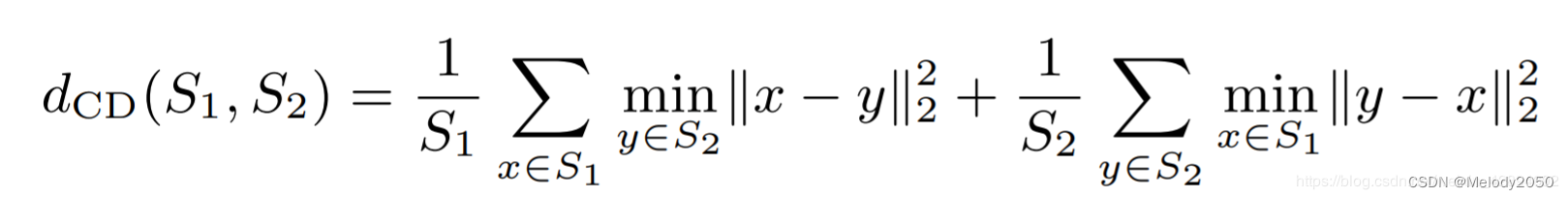
以上公式的S1,S2分别表示两组3D点云。
- 第一项代表S1中任意一点x 到S2 的最小距离之和
- 第二项则表示S2 中任意一点y 到S1 的最小距离之和。
如果该距离较大,则说明两组点云区别较大;如果距离较小,则说明重建效果较好。一般来说,该距离用作3D重建网络的损失函数。
DefTet
论文借鉴了DefTet的思路。
深度MT
3D表示
论文使用了以可变形的四面体编码的SDF来表示形状。网格将每个立方体给四面体化,每个单位都是有4个点和边的四面体。
- DefTet是用四面体上的occupancy来编码的,而本论文是用四面体各点的SD值来编码的。
- 使用SD值而不是occupancy值,可以为底层表面提供更多的灵活性。为了更好的效果,本文还会对表面作细分。
- 本文使用MT层,将基于SD的隐式表达转换为三角型的mesh。
- 最终mesh会被转换为具有可微细分表面模块的参数表面。
可变性四面体
本文利用了Gao的思路,用一组四面体来表示物体。每个四面体都由4个顶点的坐标来表示。每个顶点 v i v_i vi的SDF值为 s ( v i ) s(v_i) s(vi)。其内部任意一个点的SDF值为4个顶点的重心插值。
物体细分
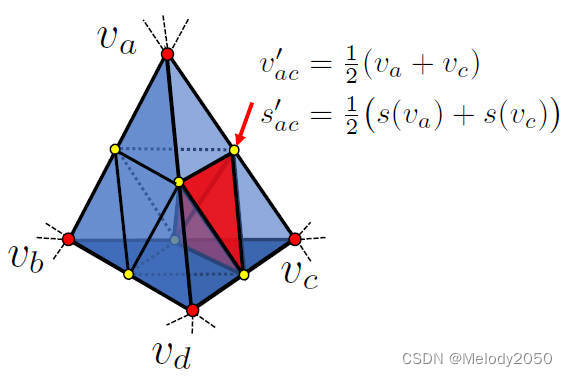
本文会从粗到细地表示物体形状。本文定义了“表面四面体” T s u r f T_{surf} Tsurf,其判断方式为,看这个四面体的四个顶点是否有不同的SDF符号——如果符号不同,说明这个四面体与物体表面相交。本文细分了 T s u r f T_{surf} Tsurf和它的直接邻居,并通过在每条边上添加中点的方式增加分辨率。
下图是一个表面四面体(蓝色),在添加中点后,会被分为8个四面体(红色)。比如图中红色箭头所指的节点 v a c ′ v^{'}_{ac} vac′,它的坐标是线段ac的中点,而SDF值为两者的平均值。
将隐式和显式表达转换的MT算法(Marching Tetrahedra)
本文使用MT算法将编码的SDF转换为显式的三角形mesh。给定四面体顶点的SDF值 { s ( v a ) , s ( v b ) , s ( v c ) , s ( v d ) } \{ s(v_a),s(v_b),s(v_c),s(v_d) \} {s(va),s(vb),s(vc),s(vd)},MT会根据 s ( v ) s(v) s(v)的符号决定四面体内部的表面拓扑形状,如下图所示。
- 4个顶点的SDF符号组合有2^4=16种情况,如果考虑旋转对称性,它们都属于3种类别
- 当表面拓扑确定时,其表面的节点坐标就被计算出来了,坐落于四面体边上按线性插值取零界值的点。
如何理解第一句?比如下图:
- 第一种情况,4个节点的SDF符号都相同,都为正或者负,共2种情况。在这种情况下,物体表面并没有与该四面体相交,所以不需要提取mesh了。
- 第二种情况,4个节点的SDF符号有两个正和两个负,符合这个类别的符号情况有6种(四面体有6条边,每条边上的两个顶点都为负,视为一种情况,有6条边就有6种情况)。
- 第三种情况,符合这个类别的符号情况有8种(3正1负有4种,3负1正也有4种)
·
三种情况加起来是2+6+8=16种情况。
如何理解第二句?我们看到,第一种情况下没有物体表面需要提取。第二、三种情况下,本文会猜测紫色的表面是那个物体表面,该表面的顶点都坐落在四面体边上。
以第三种情况为例, v a v_a va和 v b v_b vb的SDF符号相反,我们假设两点之间的SDF值是线性变化的,而mesh表面的SDF值都为0,所以我们猜测边ab的零界点 v a b ′ v_{ab}^{'} vab′应该也位于mesh表面。
所以,第三种情况的3个零值点生成一个mesh表面,第二种情况的4个零值点会组成两个mesh表面。

零界点的意思如下图所示,一个曲线与0值线的相交点成为零界点,其wiki为Zero crossing。

而零值点
v
a
b
′
v_{ab}^{'}
vab′是如何计算出来的?首先v_a和v_b的SDF值为
s
(
v
a
)
s(v_a)
s(va)和
s
(
v
b
)
s(v_b)
s(vb)。
那么线段ab上任意一点
v
c
v_c
vc的SDF值为
s
(
v
c
)
s(v_c)
s(vc),有
s
(
v
c
)
=
α
s
(
v
a
)
+
(
1
−
α
)
s
(
v
b
)
s(v_c)=\alpha s(v_a) + (1-\alpha ) s(v_b)
s(vc)=αs(va)+(1−α)s(vb)。
其中
α
\alpha
α是
v
c
v_c
vc到
v
a
v_a
va的距离比例,参考线性插值法 ,它也同时等于在x、y、z轴上映射的比例。
设 s ( v c ) = 0 s(v_c)=0 s(vc)=0,带入上式可得:
0 = α ( s ( v a ) − s ( v b ) ) + s ( v b ) α = s ( v b ) s ( v b ) − s ( v a ) , 1 − α = − s ( v a ) s ( v b ) − s ( v a ) \begin{aligned} 0 &= \alpha(s(v_a)-s(v_b)) + s(v_b) \\ \alpha &= \frac{s(v_b)}{s(v_b)-s(v_a)}, 1-\alpha = \frac{-s(v_a)}{s(v_b)-s(v_a)} \end{aligned} 0α=α(s(va)−s(vb))+s(vb)=s(vb)−s(va)s(vb),1−α=s(vb)−s(va)−s(va)
将
α
\alpha
α取值带回上文,得到:
v
a
b
′
=
α
s
(
v
a
)
+
(
1
−
α
)
s
(
v
b
)
=
s
(
v
b
)
s
(
v
b
)
−
s
(
v
a
)
v
a
+
−
s
(
v
a
)
s
(
v
b
)
−
s
(
v
a
)
v
b
=
s
(
v
b
)
v
a
−
s
(
v
a
)
v
b
s
(
v
b
)
−
s
(
v
a
)
\begin{aligned} v_{ab}^{'}&= \alpha s(v_a) + (1-\alpha ) s(v_b) \\ &= \frac{s(v_b)}{s(v_b)-s(v_a)}v_a+ \frac{-s(v_a)}{s(v_b)-s(v_a)}v_b \\ &= \frac{s(v_b)v_a-s(v_a)v_b}{s(v_b)-s(v_a)} \end{aligned}
vab′=αs(va)+(1−α)s(vb)=s(vb)−s(va)s(vb)va+s(vb)−s(va)−s(va)vb=s(vb)−s(va)s(vb)va−s(va)vb
计算结果与论文中的公式一致。
有的论文认为当 s ( v a ) = s ( v b ) s(v_a)=s(v_b) s(va)=s(vb)时,会阻止物体面变化。但是本文发现,模型只会在两者不相等时才会计算,所以在训练时,模型能够根据损失计算梯度,回传到节点位置和SDF值。
表面细分
有了mesh后,我们可以使用表面细分模块进一步增强模型的生成能力。Loop Subdivision
Charles Loop. Smooth subdivision surfaces based on triangles。
论文地址 https://charlesloop.com/thesis.pdf
DMTet: 3D生成模型
该网络的输入为 x x x(点云或者粗体素),输出为高分辨率的3D mesh M M M。
下图是DMTet的生成器和鉴别器架构。生成器有两部分,一部分使用MLP生成预测,另一部分使用GCN来细化表面。

损失函数
分为3部分,surface对齐损失、对抗损失、正则化损失。
采集点云,计算Chamber DIstance和normal direction loss
后者会找到点p以及相关的点q,以及它们所在mesh的法线,法线长度应当为1,计算它们的夹角cos值。cos越小越好,所以1-cos就是normal损失了。
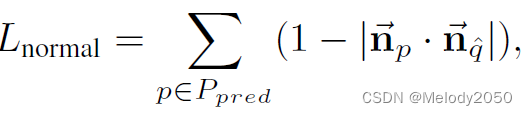
根据Mesh Normals,在大部分情况下,当提到法线时,其长度都是单位1,因为我们只关心其方向,不关心长度。
The second thing worth mentioning is that n → \overrightarrow{n} n is not unit length. It’s length is proprtional to the area of the triangle. In most applications when we discuss normal vectors we assume that they have been normalized, since it only the direction we care about, not the length. However for what comes next it is useful to keep the length as is.
对抗损失采用LSGAN损失