文章目录
- PU-Net: Point Cloud Upsampling Network
- 网络架构
- 训练数据生成
- 点特征嵌入
- Feature Expansion
- Cfoordinate Reconstruction
- 端到端训练
- Joint Loss Function
PU-Net: Point Cloud Upsampling Network
网络架构
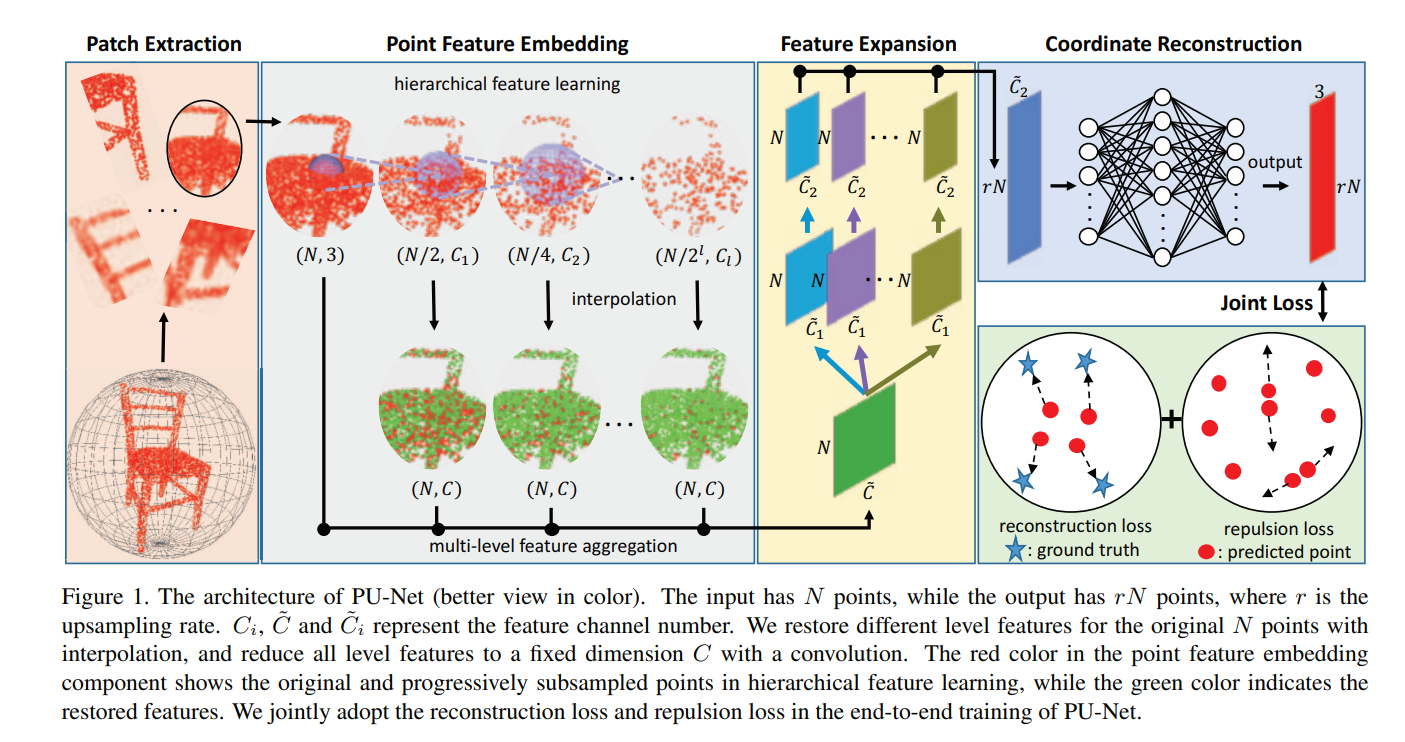
PU-Net有四个组件:patch extraction, point feature embedding, feature expansion和coordinate reconstruct。
patch extraction:从给定的一组先验3D模型中提取不同比例和分布的点块。
point feature embedding:通过分层特征学习和多层次特征聚合将原始3D坐标映射到特征空间。
feature expansion:扩展特征数量。
coordinate reconstruct:用一系列全连接层重建输出点云的三维坐标。
训练数据生成
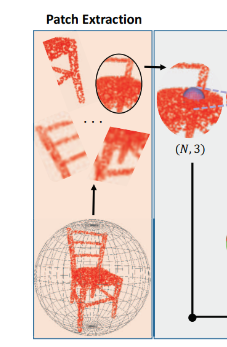
为了学习点云中的局部几何图形,作者采取基于分块的方法来训练网络。首先,在这些对象点云的表面上随机选择 M M M个点。然后从每个选定的点开始,在对象上生长出一个曲面分块,使得分块上的任何点都在曲面上与选定点的特定的测地线距离( d d d)内。最后,使用Poisson disk采样在每个面片上随机生成 N ^ \hat{N} N^个点,作为分块上的参考真实点云,而输入点在每个训练时期以 r r r的下采样率从真实点集合随机采样。
点特征嵌入
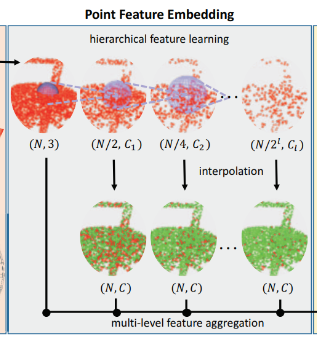
分层特征学习:
Pu-Net采用PointNet++中提出的分层特征学习机制作为网络的开端,逐步捕获层次结构中不断增长的尺度特征。
多级特征聚合
Pu-Net首先通过PointNet++中的插值方法从下采样的点特征中恢复所有原始点的特征,等级为 l l l的插值点 x x x的特征计算为:
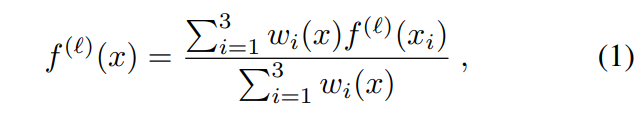
其中 w i ( x ) 1 / d ( x , x i ) w_i(x)1/d(x,x_i) wi(x)1/d(x,xi)为逆距离权重, x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3为 x x x的三个最近邻点。然后使用1x1的卷积减少不同级别的内插特征到相同维度 C C C。最后将各个级别的特征连接,得到最终的点特征 f f f
Feature Expansion
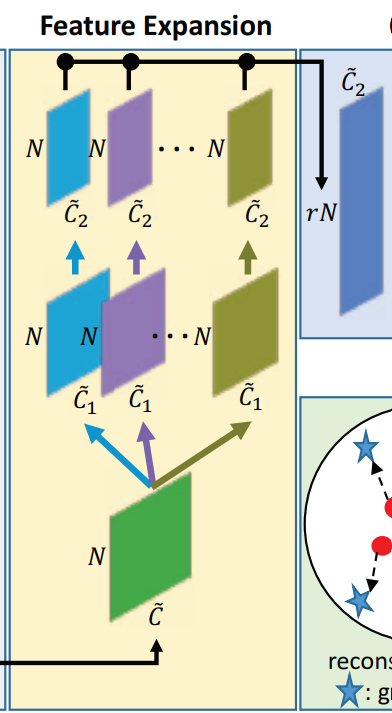
假使
f
f
f的维度为
N
×
C
~
N\times\tilde{C}
N×C~,
N
N
N为输入点数,
C
~
\tilde{C}
C~为连接的点特征的维度。特征扩展层将输出
r
N
×
C
~
2
rN\times\tilde{C}_2
rN×C~2的特诊
f
′
f'
f′,其中
r
r
r为上采样率.
基于sub-pixel convolution layer,PU-Net的上采样表示为:
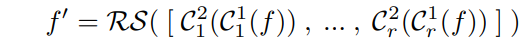
其中
C
i
1
(
⋅
)
\mathcal{C}_i^1(\cdot)
Ci1(⋅)(每个特征集共享参数)和
C
i
2
(
⋅
)
\mathcal{C}_i^2(\cdot)
Ci2(⋅)(每个特征集参数不同)表示对
f
f
f进行的两次1x1卷积。
R
S
(
⋅
)
\mathcal{RS}(\cdot)
RS(⋅)将
N
×
r
C
~
2
N\times r\tilde{C}_2
N×rC~2的张量reshape为
r
N
×
C
~
2
rN\times \tilde{C}_2
rN×C~2。
Cfoordinate Reconstruction
使用全连接网络将 N × C ~ 2 N\times \tilde{C}_2 N×C~2的扩展特征变换为 N × 3 N\times3 N×3。

端到端训练
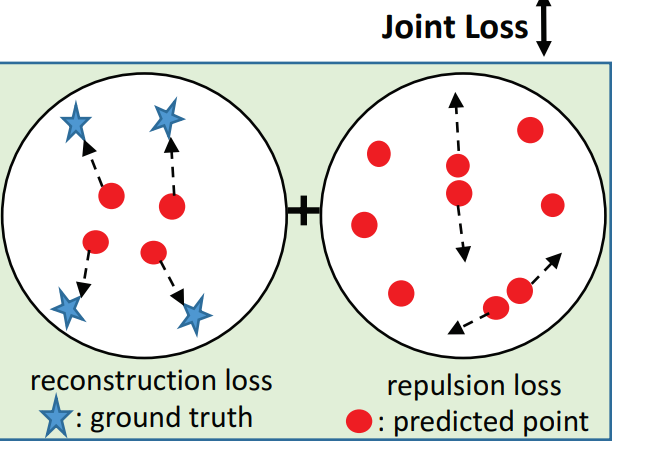
Joint Loss Function
重建损失使用Earth Mover’s distance(EMD):
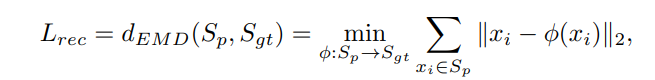
其中 S p S_{p} Sp为predicted point cloud; S g t S_{gt} Sgt为参考点云。 ϕ : S p → S g t \phi:S_p\rightarrow S_{gt} ϕ:Sp→Sgt为双射映射
尽管具有重建损失的训练可以在基础对象表面上生成点,但生成的点往往位于原始点附近。为了更均匀地分布所生成的点,Pu-Net还包含一个排斥损失,表示为:

其中 N ^ = r N \hat{N}=rN N^=rN为输出点的数目, K i K_{i} Ki为 x i x_i xik个最近邻点的索引。 ∣ ∣ ⋅ ∣ ∣ ||\cdot|| ∣∣⋅∣∣为L2范数。递减函数 η ( r ) = − r \eta(r)=-r η(r)=−r作为排斥项(距离越小值越大),避免 x i x_i xi离其他点 K i K_{i} Ki太近。 w ( r ) = e − r 2 / h 2 w(r)=e^{-r^2/h^2} w(r)=e−r2/h2为权重因子。
最终的端到端训练损失函数:
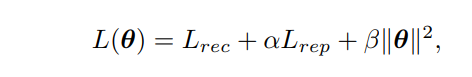
其中
θ
\bold{\theta}
θ为网络参数,
α
\alpha
α和
β
\beta
β为权重。