CS224W—02 Node Embeddings

Node Embeddings概念

传统的图机器学习：

• 给定一个输入图，抽取节点、边和图级别特征, 学习一个能将这些特征映射到标签的模型(像SVM， NN…)
• 这个抽取不同级别特征的过程，就是特征工程feature engineering
• 学习到模型后拿来预测就是具体的下游预测任务

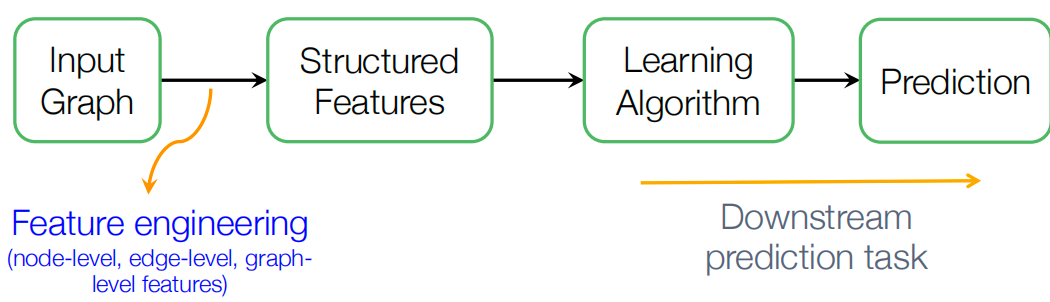
图表示学习可以减轻每次做特征工程的需求，自动的学习到特征。

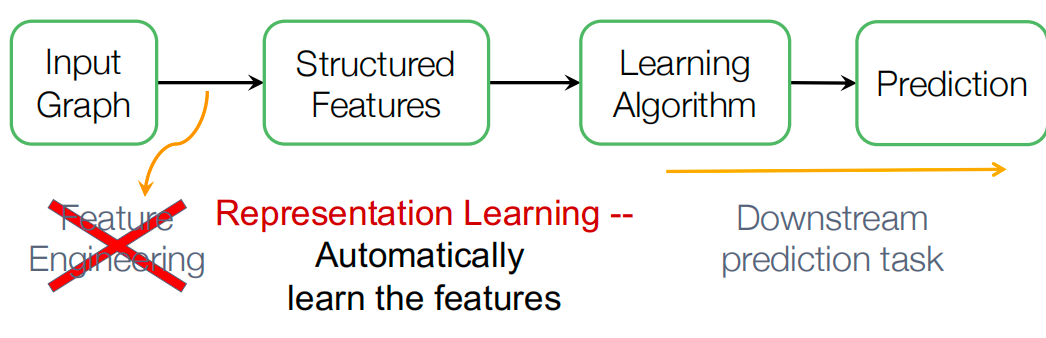
目标：图机器学习的高效的任务无关特征学习。对于图，要抽取到任务无关的的特征，这样下游任务不同也能用。

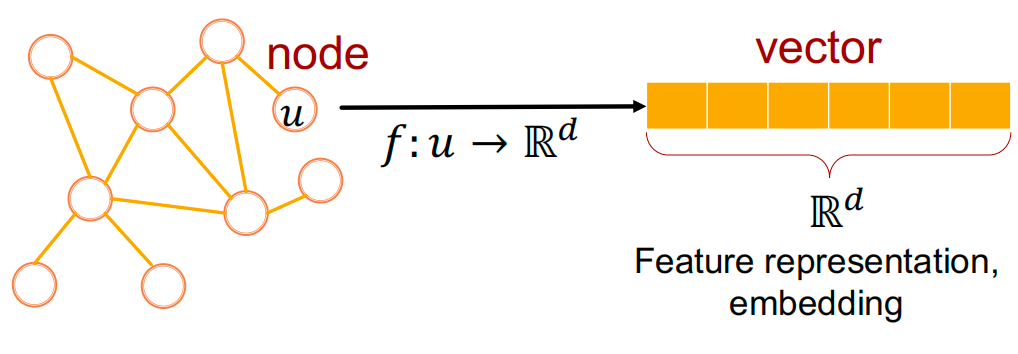
如上图，就是将节点 𝑢 ，经过函数 𝑓 ， 映射成向量。这就是特征表示或者更具体地说是embedding。

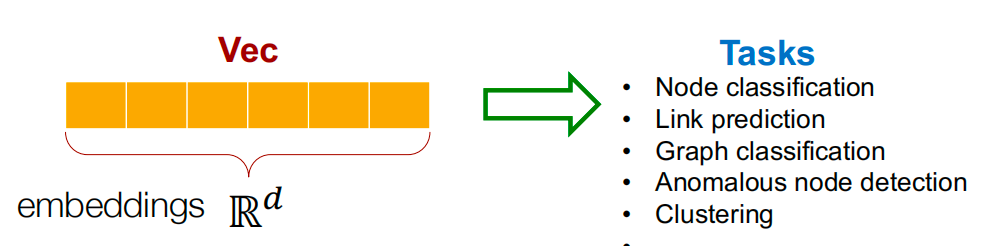
为什么需要embedding？

1. 可视化和理解：图结构通常是高维的，难以直接可视化。通过图嵌入，可以将节点映射到一个低维空间（通常是二维或三维），使得网络的结构和关系更容易被观察和理解。

2. 相似性度量：在网络中，节点之间的相似性是一个重要的概念。通过图嵌入，可以将这种相似性转化为向量空间中的距离。节点的嵌入向量越接近，它们在网络中的行为和特征就越相似。这有助于识别网络中的社区结构或相似节点。

3. 编码网络信息：图嵌入可以将网络的结构信息编码到向量中。这意味着节点的嵌入向量不仅包含了它们自身的信息，还包含了它们与网络中其他节点的关系。这对于理解节点在网络中的角色和功能至关重要。

4. 下游任务应用：图嵌入生成的向量可以作为输入特征，用于各种机器学习任务。

5. 处理大规模数据：大规模图数据的处理和分析常常面临计算和存储的挑战。图嵌入可以将图数据转换为更紧凑的向量形式，从而减少存储需求和加速计算过程。

6. 增强模型性能：在许多机器学习模型中，输入特征的质量和表示方式对模型性能有显著影响。图嵌入通过将图数据转换为向量，可以提高模型在处理图结构数据时的准确性和效率。

Encoder and Decoder

Setup

假设我们有一个无向图 $G$：

• $V$ 是顶点集合。
• $A$ 是邻接矩阵（假设为二进制）。
• 为简化起见：不使用节点特征或额外信息。

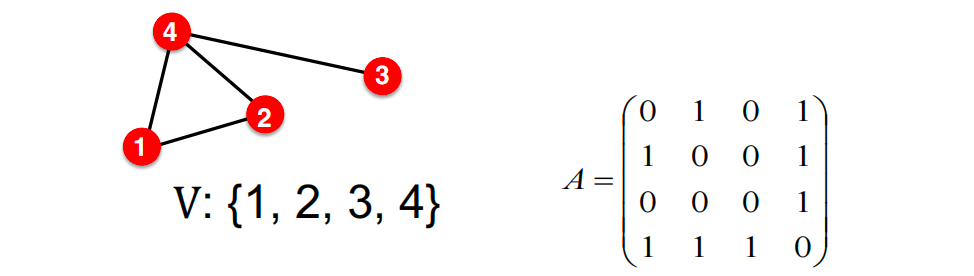
Node Embeddings

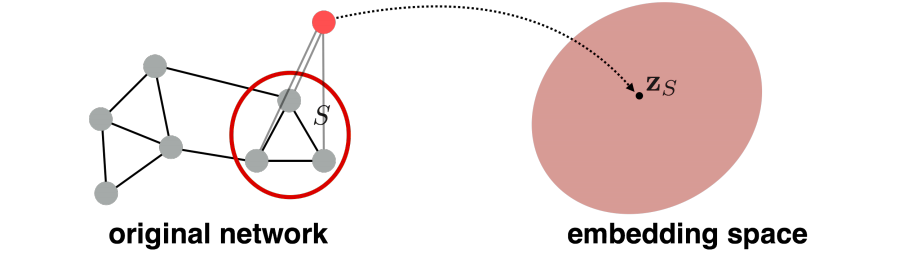
目标：编码节点，以便embedding space（如点积）中的相似度近似于图中的相似度。

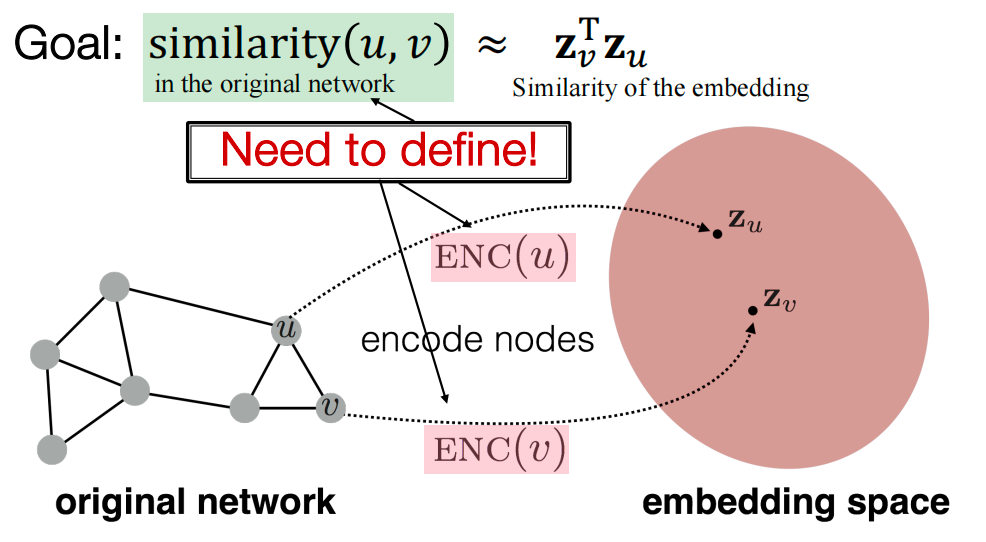
如上图中，原始的网络中的邻居节点u、v ，编码到embedding空间后，对应的 ${\mathbf{z}}_u,{\mathbf{z}}_v$ 也要相近。

Learning Node Embeddings

过程：

1. 编码器将节点映射到嵌入

2. 定义一个节点相似性函数（即，在原始网络中的相似性度量）

3. 解码器 $DEC$ 将嵌入映射到相似性得分

4. 优化编码器的参数，使得：$$\text{similarity}(u,v)\approx {\mathbf{z}}_v^T{\mathbf{z}}_u$$

Encoder: 映射每个节点到低维度向量。

相似度函数: 明确编码后向量空间和原始网络是怎样的映射关系，如上图，就是原始网络中u和v的相似度和这两个节点embedding后的点积是如何对应的。

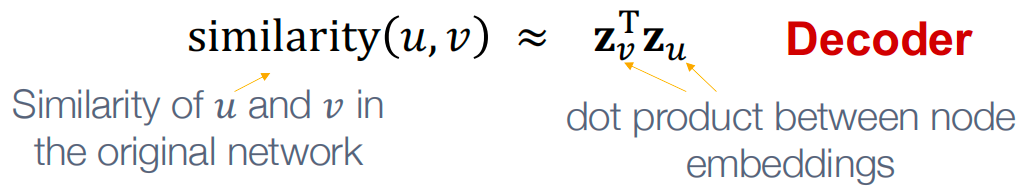
Shallow Encoding

最简单的编码方法：编码器仅仅是一个嵌入查找。

$\text{ENC}(v)={\mathbf{z}}_v=\mathbf{Z}\cdot v$，其中：

• $\mathbf{Z}\in {\mathbb{R}}^{d\times |V|}$ 表示嵌入矩阵，每一列是一个节点的嵌入向量。
• v ∈ { 0 , 1 } ∣ V ∣ v \in \{0, 1\}^{|V|} v∈{0,1}∣V∣ 是指示向量，除了在第 $v$ 列有一个1表示节点 $v$ 外，其他位置都是0。

得到嵌入矩阵的方法有 DeepWalk, node2vec等。

Encoder + Decoder Framework

Shallow Encoding：嵌入查找

• 需要优化的参数：$\mathbf{Z}$，其中包含所有节点 $u\in V$ 的节点嵌入 ${\mathbf{Z}}_u$
• 我们将在图神经网络（GNNs）中介绍 deep encoders

解码器：基于节点相似性

• 目标：对于相似的节点对 $(u,v)$，最大化 ${\mathbf{z}}_v^T{\mathbf{z}}_u$

上述方法的关键点是怎么定义节点相似度 ？接下来将用随机游走来学习获得节点相似度，和怎样为该相似度指标优化embedding。

Random Walk Approaches for Node Embeddings

符号

向量 ${\mathbf{z}}_u$：节点 $u$ 的嵌入。
概率 $P(v\mid {\mathbf{z}}_u)$：

• 基于 ${\mathbf{z}}_u$ 的模型预测。
• 从节点 $u$ 开始的随机游走中访问节点 $v$ 的（预测）概率。

用于产生预测概率的非线性函数：

• Softmax 函数：将 $K$ 个实值（模型预测）转换为 $K$ 个总和为1的概率：$S(\mathbf{z})[i]=\frac{e^{\mathbf{z}[i]}}{{\sum }_{j=1}^K{e}^{\mathbf{z}[j]}}$。
• Sigmoid 函数：将实值转换为范围在 $(0,1)$ 内的S形函数，表示为 $\sigma (x)=\frac{1}{1+e^{-x}}$。

Random Walk

给定一个图和一个起始点，我们随机选择一个相邻点，然后移动到这个相邻点；接着我们随机选择这个点的一个相邻点，并移动到它，依此类推。这样访问点的（随机）序列是图上的随机游走（Random Walk）。

Random Walk Embeddings：
$${\mathbf{z}}_u^T{\mathbf{z}}_v=\mathbf{z}和\mathbf{v}一起出现在图中的随机游走上的概率$$

1. 使用某种随机游走策略$R$，从节点$u$开始估计访问节点$v$的概率$P_R(v|u)$。
2. 这个概率就是节点u和v的相似度，我们可以根据这个概率来优化embedding，在embedding空间的相似度，这里 dot product=cos⁡(𝜃) ,就是编码的随机游走相似度。

优势：

• 可解释性：灵活的随机定义节点相似性，该定义结合了局部和更高阶邻域信息。
  • 思想：如果从节点$\alpha$开始的随机游走以高概率访问节点$\beta$，则$\alpha$和$\beta$是相似的（高阶多跳信息）。
• 高效性：在训练时不需要考虑所有节点对；只需要考虑在随机游走中共同出现的对。

Unsupervised Feature Learning

直觉：在$d$维空间中找到节点的嵌入，以保持相似性。

思路：学习节点嵌入，使得在网络中相邻的节点彼此靠近。

给定一个节点$u$，我们如何定义相邻节点？$N_R(u)$ … 通过某种随机游走策略$R$获得的$u$的邻域

给定图$G=(V,E)$，我们的目标是学习一个映射$f:u\to {\mathbb{R}}^d$：$f(u)={\mathbf{z}}_u$

对数似然目标：${\text{arg max}}_z{\sum }_{u\in V}\log \left(P(N_R(u)|{\mathbf{z}}_u)\right)$

• 其中$N_R(u)$是通过策略$R$得到的节点$u$的邻域。给定节点$u$，我们希望学习特征表示，这些表示能够预测其随机游走邻域$N_R(u)$中的节点。

Random Walk Optimization

1. 从图中的每个节点$u$开始，使用某种随机游走策略$R$运行短的固定长度随机游走。
2. 对于每个节点$u$，收集$N_R(u)$，即从$u$开始的随机游走中访问的节点的多重集。
3. 根据以下方式优化嵌入：给定节点$u$，预测其邻居$N_R(u)$。

等价地，$ \arg\min_z \mathcal{L} = \sum_{u \in V} \sum_{v \in N_R(u)}-\log(P(v \mid z_u)) $

直觉：优化嵌入$z_u$以最小化随机游走邻域$N(u)$的负对数似然。

使用softmax参数化$P(v\mid z_u)$：
$$P(v\mid {\mathbf{z}}_u)=\frac{\exp ({\mathbf{z}}_u^T{\mathbf{z}}_v)}{{\sum }_n\exp ({\mathbf{z}}_u^T{\mathbf{z}}_n)}$$

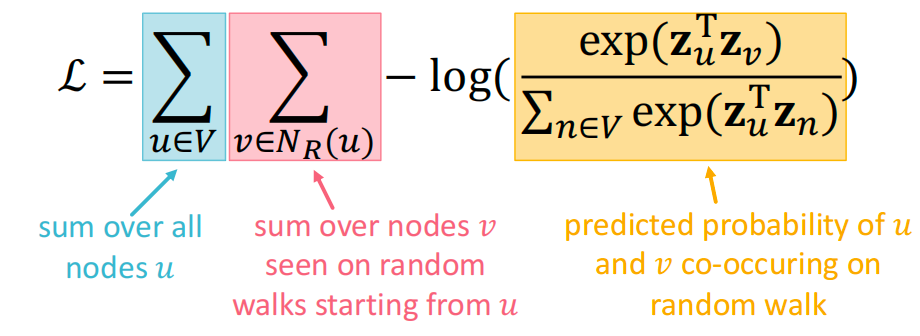
计算复杂度高：$O(|V{|}^2)$

解决方法： 负采样。这里将softmax替换为sigmoid, 近似得到:
$$\begin{gathered} -\log \left(\frac{\exp ({\mathbf{z}}_u^T{\mathbf{z}}_v)}{{\sum }_n\exp ({\mathbf{z}}_u^T{\mathbf{z}}_n)}\right)\approx \\ \log \left(\sigma \left({\mathbf{z}}_u^{\mathrm{T}}{\mathbf{z}}_v\right)\right)+\sum _{i=1}^k\log \left(\sigma \left(-{\mathbf{z}}_u^{\mathrm{T}}{\mathbf{z}}_{n_i}\right)\right),n_i\sim P_V \end{gathered}$$
负采样就是将分母归一化部分中所有节点 𝑛 替换为随机采样得到的 k个负样本 $n_i$ ，即不在random walk上的样本.

对于k（负样本数量）的两个考虑：

1. 更高的k值提供更稳健的估计
2. 更高的k值对应于对负事件的更高偏差：实践中k值通常为5到20。
3. 负样本可以是任意节点还是仅限于不在游走中的节点？人们通常采样任意节点（出于效率考虑）。

使用随机梯度下降优化目标：
$$\mathcal{L}=\sum _{u\in V}\sum _{v\in N_R(u)}-\log (P(v\mid {\mathbf{z}}_u))$$
应该使用什么策略进行随机游走呢？最简单的想法：直接固定长度，每个节点都无偏的随机游走。 但问题是这样的策略使得相似度有非常大的局限性。2014DeepWalk：https://arxiv.org/pdf/1403.6652

Node2Vec

2016node2vec：https://cs.stanford.edu/~jure/pubs/node2vec-kdd16.pdf

• 目标：将具有相似网络邻域的节点嵌入到特征空间中靠近的位置。
  我们将这个目标构建为一个最大似然优化问题，独立于下游预测任务。
• 关键观察：灵活的网络邻域$N_r(u)$的概念导致丰富的节点嵌入。
• 开发有偏的二阶随机游走$R$来生成节点$u$的网络邻域$N_R(u)$。

思想：使用稳定的有偏随机游走来权衡网络的局部和全局视图。

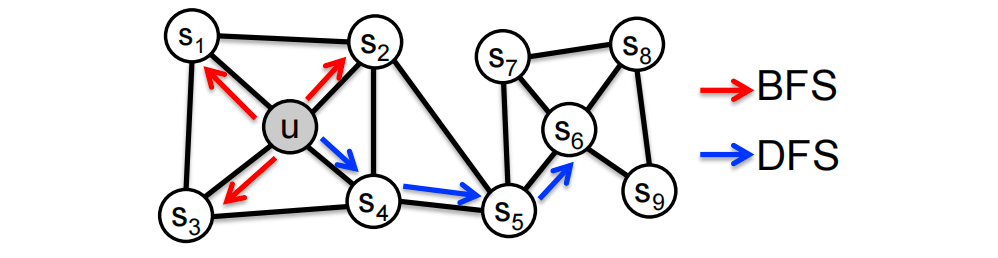
长度为3的游走（$N_R(u)$的大小为3）：

• N B F S ( u ) = { S 1 , S 2 , S 3 } N_{BFS}(u) = \{ S_1, S_2, S_3 \} NBFS​(u)={S1​,S2​,S3​}：局部微观视角
• N D F S ( u ) = { S 4 , S 5 , S 6 } N_{DFS}(u) = \{ S_4, S_5, S_6 \} NDFS​(u)={S4​,S5​,S6​}：全局宏观视角

给定节点$u$生成邻域$N_R(u)$的有偏固定长度随机游走$R$。随机游走有两个参数：

• 返回参数$p$：返回前一个节点
• 进出参数$q$：从前一个节点向外（深度优先搜索DFS）与向内（广度优先搜索BFS）移动：直观上，$q$是BFS与DFS的“比例”

接下来，我们指定如何执行有偏随机游走的单步。随机游走就是这些步骤的序列。

Biased Random Walk

有偏的2阶随机游走探索网络邻居节点：

• 假设通过边 $(s_1,w)$ 到达 $w$ 节点

• 那么现在w节点的邻居节点可能是 $s_1,s_2,s_3$ 。这跟最开始的起点 $s_1$ 的意义是不一样的。

  

  

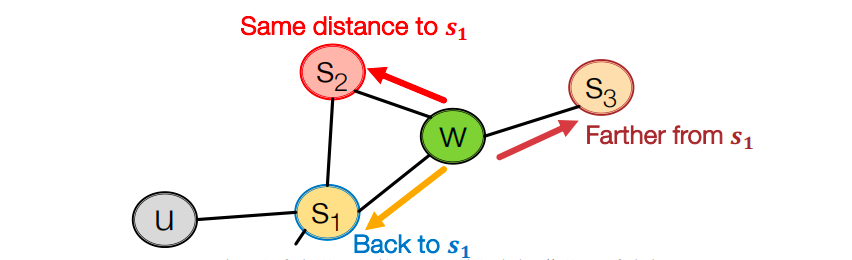
• 通过边 $(s_1,w)$走到 $w$ 节点，下一步跳到哪？ 如图跳到下一个节点的的概率是不一样的。(注意，$1/p$, $1/q$,1 不是归一化的概率，加起来和不为1)

• $p$，$q$是模型的转移概率。

如上图所示，前一步通过边$(s_1,w)$到达节点$w$。现在走到的节点$w$，邻居节点有$s_1$，$s_2$，$s_3$，$s_4$。具体怎么设计$p$，$q$概率呢？

根据上一跳节点和下一跳节点的距离设计，说到距离，就要明确这两点在哪？上一跳节点为$s_1$，下一跳为 $s_1,s_2,s_3,s_4$。

论文中提到：
$${\alpha }_{pq}(t,x)=\{\begin{array}{ll}\frac{1}{p}& \text{ if }{d}_{tx}=0\\ 1& \text{ if }{d}_{tx}=1\\ \frac{1}{q}& \text{ if }{d}_{tx}=2\end{array}$$
$t$表示上一跳节点，$x$表示未来要走的节点，$d_{tx}$表示这两个节点之间的距离。所以上图中的转移概率如下：

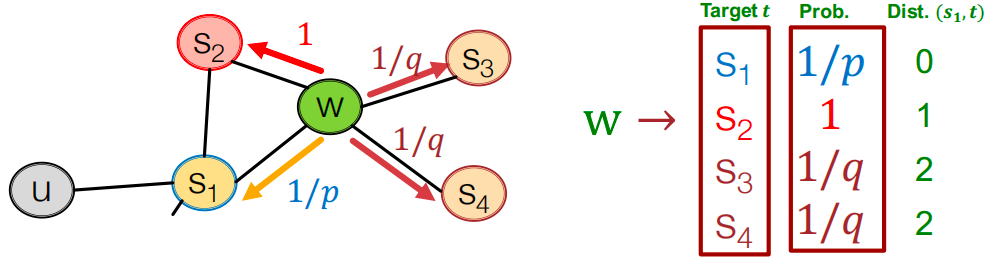
• 类似BFS的游走：较小的p值，那么 1/𝑝 就较大，会回到上一跳节点。
• 类似DFS的游走：较小的q值，会往跟上一跳较远的距离跳。

Algorithm

1. 计算边的转移概率：对于每条边$(s_i,w)$，我们计算基于$p,q$的边游走概率$(w,\cdot )$。
2. 模拟从每个节点 $u$ 开始长度为 $l$ 的 $r$ 次随机游走。
3. 使用随机梯度下降优化node2vec目标。（目标和上面的一样）

线性时间复杂度：所有3个步骤都可以单独并行化。

Summary

• 没有一种方法在所有情况下都是最优的。例如，node2vec在节点分类上表现更好，而其他方法在链接预测上表现更好。
• 随机游走方法通常更有效率。
• 一般来说：必须选择与你的应用程序匹配的节点相似性定义。

Embedding Entire Graphs

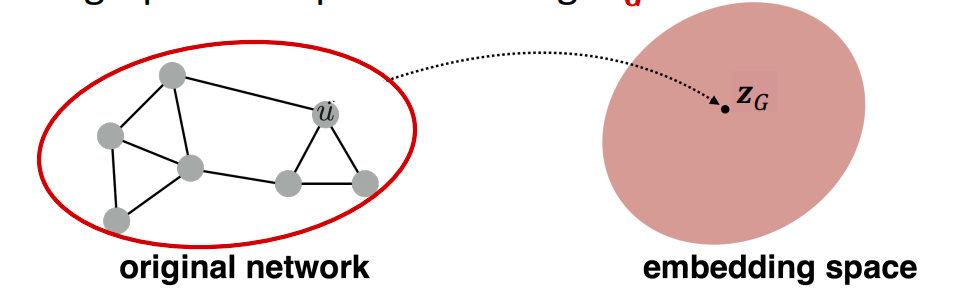
• 目标：把一个子图或者一张图嵌入到特征空间去，得到图的embedding: ${\mathbf{z}}_G$
• 具体任务：对有毒和无毒分子分类；鉴别异常的图

方法1

简单（但有效）的方法1：https://arxiv.org/abs/1509.09292
在（子）图$G$上运行标准图嵌入技术。然后只需将（子）图$G$中的节点嵌入求和（或平均）。
$${\mathbf{z}}_G=\sum _{v\in G}{\mathbf{z}}_v$$

方法2

引入一个”虚拟节点“来表示子图，然后再对其用node embedding。https://arxiv.org/abs/1511.05493

Matrix Factorization and Node Embeddings

回忆：编码器是一个嵌入查找。

$\text{ENC}(v)={\mathbf{z}}_v=\mathbf{Z}\cdot v$，其中：

• $\mathbf{Z}\in {\mathbb{R}}^{d\times |V|}$ 表示嵌入矩阵，每一列是一个节点的嵌入向量。
• v ∈ { 0 , 1 } ∣ V ∣ v \in \{0, 1\}^{|V|} v∈{0,1}∣V∣ 是指示向量，除了在第 $v$ 列有一个1表示节点 $v$ 外，其他位置都是0。

最简单的节点相似性：如果节点$u$和$v$由一条边连接，它们就是相似的，这对应于图邻接矩阵$A$中的$(u,v)$项。因此，${\mathbf{Z}}^T\mathbf{Z}=A$。

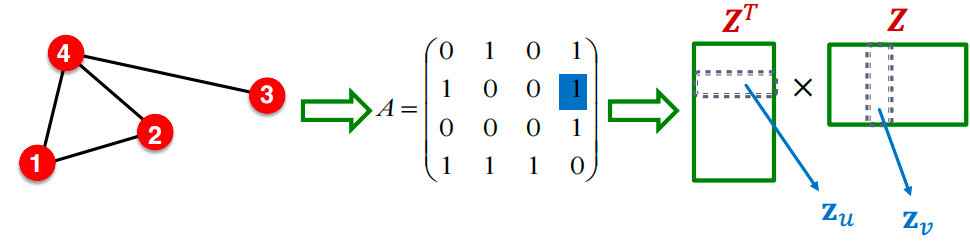
嵌入维度 $d$（矩阵 $Z$ 的行数）远小于节点数 $n$。精确分解 $A=Z^{T}Z$ 通常是不可能的。然而，我们可以近似学习 $Z$。

• 我们优化 $Z$ 以最小化 $A-Z^{T}Z$ 的 $L2$ 范数（Frobenius范数）。
• 注意今天使用了softmax而不是 $L2$。但用 $Z^{T}Z$ 近似 $A$ 的目标是相同的。
• 结论：内积解码器，其中节点相似性由边连接性定义，等同于矩阵 $A$ 的分解。

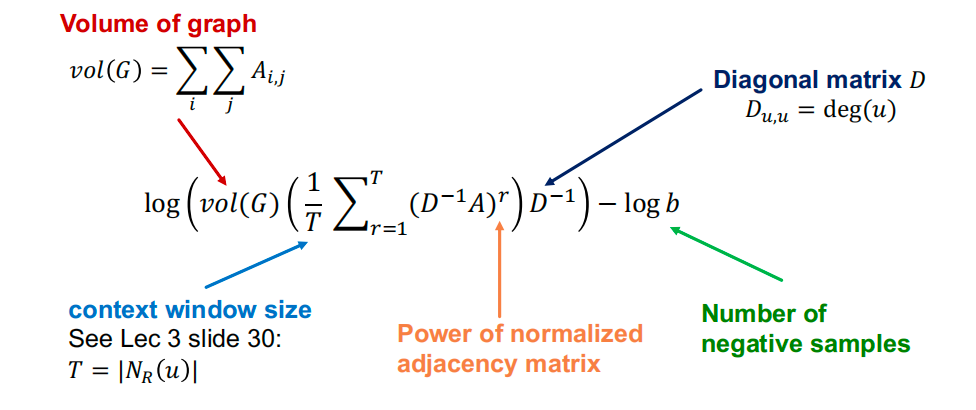
DeepWalk 等同于以下复杂矩阵表达式的矩阵分解:https://keg.cs.tsinghua.edu.cn/jietang/publications/WSDM18-Qiu-et-al-NetMF-network-embedding.pdf
$$\log \left(\mathrm{vol}(G)\left(\frac{1}{T}\sum _{r=1}^T{\left(D^{-1}A\right)}^r\right)D^{-1}\right)-\log b$$

总结与局限

怎么使用节点的embeddings ${\mathbf{z}}_i$ ：

• 聚类/社区发现: 聚类${\mathbf{z}}_i$点
• 节点分类：基于${\mathbf{z}}_i$预测节点i的标签
• 边预测： 基于 $({\mathbf{z}}_i,{\mathbf{z}}_j)$ 预测边 $(i,j)$ , 可以通过平均点积等方法 求embeddings的差值
• 图预测：通过聚合节点embeddings或虚拟节点游走获得的图embedding $z_G$ 来预测图的标签

局限性：

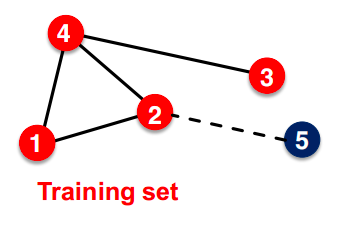
1. 无法为训练集中不存在的节点获得嵌入。无法应用于新图、演化图：测试时新增节点5（例如，社交网络中的新用户）。无法使用DeepWalk或node2vec计算其嵌入。需要重新计算所有节点嵌入。
2. 无法捕捉结构相似性。节点1和11在结构上相似 ： 都是一个三角形的一部分，度数为2。然而，它们具有非常不同的嵌入。
   从节点1随机游走到节点11的可能性很小。DeepWalk和node2vec没有捕捉到结构相似性。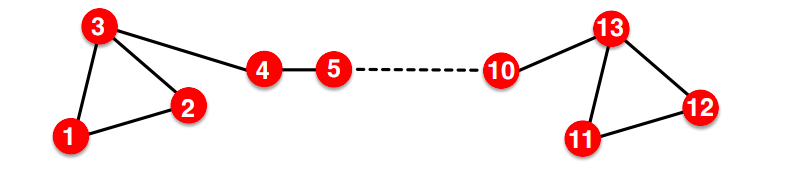
3. 无法利用节点、边和图特征。特征向量（例如，在蛋白质-蛋白质交互图中的蛋白质属性）。DeepWalk/node2vec嵌入没有结合这些节点特征。解决这些限制的方案：深度表示学习和图神经网络。

参考资料

• CS224W笔记-3-1. Node Embeddings - aigonna的文章 - 知乎https://zhuanlan.zhihu.com/p/486094620
• https://web.stanford.edu/class/cs224w/