快速排序
- 递归版本
- 挖坑法
- Hoare法
- 优化
- 非递归
相信即使大家并不知道快速排序究竟是个啥,但也一定听说过快排,今天我来给兄弟们讲讲快速排序!
递归版本

快速排序的思想就是找基准,就比如我们以数组中的第一个数字12为基准,我们从最后往前面找,如果找到一个比12小的数字就用它覆盖12,但是如果我们不提前储存一份12的话,后面就找不到这个数据了,我们使用覆盖的话就是使用的挖坑法,此时场上有两个9,这是显然不可以的,所以我们就从头开始往后面找,找到一个比12大的数字放到9位置…最后达到的效果必然是左右相遇,那么前面的就全都是比基准小的数字,后面都是比基准大的数字了.
挖坑法
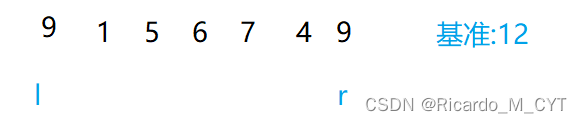
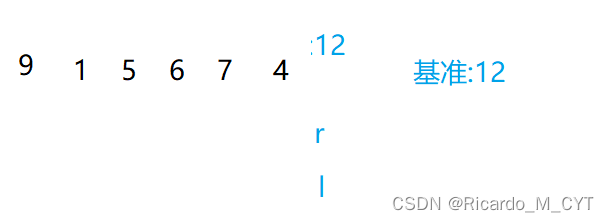
第一趟找基准找好了,然后呢?我们现在已经确定了一个位置,那这个位置的左右是不是可以使用同样的方法递归下去呢?递归条件就是左边不能跑到右边去.
//这里是为了参数的统一才
public void quickSort(int[]arr){
quick(arr,0,arr.length-1);
}
private void quick(int[]arr,int left,int right){
//递归的终止条件
if(left>=right)return;
int index=partition1(arr,left,right);
quick(arr,left,index-1);
quick(arr, index+1,right);
}
private int partition(int[] array,int left,int right){
int tmp=array[left];
//在找基准的时候,有很大可能是要进行多次数据调整的
while(left<right){
while(left<right&&array[right]>=tmp){
//找数据的时候也不能够越界,还有就是这里的还有下面的等号
//至少要写一个,不然会前后相同的数据反复交换
right--;
}
swap(array,left,right);
while(left<right&&array[left]<=tmp){
left++;
}
swap(array,left,right);
}
//从循环出来就意味着左右相遇了
array[left]=tmp;
return left;
}
Hoare法
挖坑法是事先留好基准的那个坑,最后再给填上,Hoare法就是先找,后面找到小的停下来,前面找到大的停下来,然后交换,要知道的是,Hoare就不是覆盖了,而是交换.
那兄弟们有没有想过,为什么不论是挖坑还是Hoare我们都是先从后面开始找比基准小的呢?因此如果我们先从前面找比基准大的数字的话,最后停下的位置找到的一定是比基准大的,交换完成后,大的就到前面了,这可不行!
private int partition1(int[] array,int left,int right){
int tmp=array[left];
int i=left;
while(left<right){
while(left<right&&array[right]>=tmp){
right--;
}
while(left<right&&array[left]<=tmp){
left++;
}
swap(array,left,right);
}
swap(array,i,left);
return left;
}
优化

我们考虑极端情况下,数据已经有序,此时我们递归的深度会很大:

如果数据很大的情况下,很有可能就会栈溢出,所以我们希望的情况是,每一次我们找到的基准都是相对中间的数字,这样子我们左右都会处于一种相对平衡的状态:

但是从我们刚才的代码中可以发现,每一次我们找的基准都是从最左边开始的,如果我们的人品不错,那么我们可以考虑从数组中随机选取一个数字,就以这个数字为基准开始找它位置,可是如果运气不太好的话,我们还是会造成上述的问题,因此我们可以使用三数取中法,首尾加中间的,这样子三数取中间作为基准的话,左右两边不至于有一边是空的.找到中间数之后和最左边的数字交换即可:
private int getMid(int[]arr,int left,int right){
int mid=(left+right)/2;
if(arr[left]>arr[right]){
if(arr[mid]>arr[left]){
return left;
}else if(arr[right]>arr[mid]){
return right;
}else {
return mid;
}
}else {
if(arr[mid]>arr[right]){
return right;
}else if(arr[left]>arr[mid]){
return left;
}else {
return mid;
}
}
}
我们还可以利用插入排序越有序越快的特性再进行优化,我们知道指数增长越到后面越是可怕,所以当我们运行到一定程度的时候,是不是数据已经趋于有序了,那此时我们直接上插入排序,排完return走人:
private void quick(int[]arr,int left,int right){
if(left>=right)return;
if(right-left+1>3){
insertSort1(arr,left,right);
return;
}
int midIndex=getMid(arr,left,right);
swap(arr,midIndex,left);
int index=partition1(arr,left,right);
quick(arr,left,index-1);
quick(arr, index+1,right);
}
非递归
一般来说非递归的方法使用起来就是循环了,此时我们需要使用到栈,使用栈的原因是因为要记录下每次快排的起始和结束位置:
public void quickSortNonR(int[] arr, int left, int right) {
Stack<Integer>stack=new Stack<>();
//基准方法不光是找到基准的位置,还会为我们直接在原数组上动刀
int index=partition(arr,left,right);
//首先我们必须给栈一个数据才可以
stack.push(0);
stack.push(index-1);
stack.push(index+1);
stack.push(right);
while(!stack.empty()){
int end=stack.pop();
int start=stack.pop();
int par=partition(arr,start,end);
//只有一个数据的话就已经有序了,不需要再排序
if(par-start>1){
stack.push(start);
stack.push(par-1);
}
if(end-par>1){
stack.push(par+1);
stack.push(end);
}
}
}
希望我的这篇博客能够帮助到大家!
百年大道,你我共勉!!!