点分治学习笔记

news2024/11/16 4:35:03

有时候我们会碰到一些树上的路径问题，如果需要处理的规模很大的话，这时候点分治是一个很好的工具，往往可以在O(nlogn)的复杂度内完成操作，一般用于离线处理问题

前置芝士

树的重心：最大子树的值最小的点叫做重心。

感性地理解一下，就是重心可以将树尽可能地平均分程若干个子树。（显然

要求重心也很简单，dfs即可

siz[]代表子树大小，mx代表最大子树的大小
void find_rt(ll id,ll fa)
{
	siz[id]=1;mx[id]=0;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		find_rt(y,id);
		mx[id]=max(mx[id],siz[y]);
		siz[id]+=siz[y];
	} 
	mx[id]=max(mx[id],nt-siz[id]);//nt代表当前树的大小
	if(mx[id]<mx[rt])
	{
		rt=id;
	}
}

点分治 

关于树上路径，其实可以分为两类：过根的，和不过根的

一个比较显然的思路是我们可以求出树中每一个点到根的距离（或者相关信息），然后将不同的子树内的点进行信息合并，我们就可以轻松解决树上过根路径。

比如考虑点对距离问题，我们分别求出每一个子树内的点的深度，然后与其它子树内的点的深度相加即可（因为此时我们只考虑过根的路径）

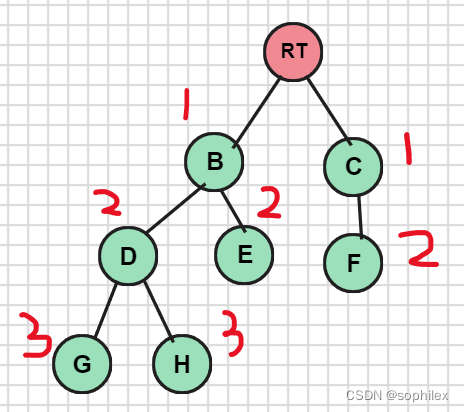
这里还有一个问题，就是不同子树间的点如何合并。如果我把整棵树都搜完了再合并，复杂度是n^2。所以这里有一个很好的思路。我们考虑一个子树一个子树去遍历。当我搜到第二个子树，前面子树的信息都保留下来，那么就可以直接操作了（这里的一个细节是我们忽略了信息具体是与谁合并，我们只关注合并后的信息，如果题目要求指出具体点对的话，应该就不是用点分治来做了），显然这样做合并不重不漏。（这里可能有点绕，看看后面的具体题目就懂了）

这是过根的路径，我们再来考虑不过根的路径。其实这种路径也可以转化为前一种，只不过对应的根节点不同罢了。处理完根节点之后，它的信息已经都合并过了，就可以删了，所以此时整棵树就变成了一个森林，我们只要对森林里的每一棵树递归进行同样的操作就可以了。但是这样做的话，复杂度是有问题的。我们考虑一条链

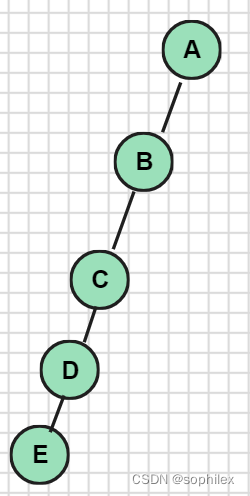
 对A进行上述操作后，子树是B，对B操作之后，子树是C，...这样的话，我们要递归n次，每次操作要O(n),复杂度就是n^2。O(n)想要再降下去有点困难，所以我们可以考虑如何降低递归次数。说白了，一条链会递归n次，是因为每次子树都是一个，如果我们能将子树尽可能分成多一点，每一个子树都小一点，复杂度就下来了。这里就可以用我们上面的重心来处理了。以重心为根对树进行处理，显然每次最大的子树大小不会超过n/2（否则我们以最大子树对应节点为根节点，最大子树会更小），所以我们的递归次数只要logn级别，整体复杂度就来到了nlogn。

点分治大致的思路就是这样，先找到树的重心，然后递归向下处理，对于每一个子树，都去重新找一个重心再递归。

例题

【模板】点分治1

点分治

大意：大小为n的树，m次询问，查询树上是否存在长度为k的路径，

1≤n≤10^4,1≤m≤100,1≤k≤10^7

思路：点分治的话复杂度是nmlogn，吃得住

先来看主代码，mx和nt之前解释过了，然后我们先找到当前树的重心（find_rt），再更新siz数组。

这里我的写法是find_rt(rt,0)，也就是在找到rt之后再跑一遍find_rt,因为原本的siz数组不是以重心为根的，而后面我们做点分治的时候还要用到siz数组，所以这里更新一下。

    //上面是输入
	mx[0]=nt=n;
	find_rt(1,0);
	find_rt(rt,0);//更新siz数组，因为现在是以一个新的点为根节点
	dfz_(rt); 
	for(int i=1;i<=m;++i)
	{
		cout<<(ans[i]?"AYE":"NAY")<<endl;
	}

具体如何进行点分治？

首先统计以该节点为根的树内的过根路径信息，然后标记vis。向下递归的时候，我们要重新找到一个子树内的重心，所以信息初始化。这里就体现了我们为什么在求重心的时候要更新siz数组，因为我们求子树的重心的时候，要用到子树的大小。

void dfz_(ll id)//点分治 
{
	calc(id);
	vis[id]=1;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		//递归 
		rt=0;mx[rt]=nt=siz[y];
		find_rt(y,0);find_rt(rt,0);//更新siz
		dfz_(rt); 
	}
}

 再看看如何统计过根的信息：

具体来说，遍历一个子树的时候，我们需要一个dis_vis[]来记录之前子树中有没有出现某一个长度的路径，如果有，该值就是1.对于当前子树，我们要找到所有长度，去与前面进行合并，所以我们再加一个d[]数组，cnt用于离散化计数。

处理完当前子树内后（get_dis）,我们暴力对答案进行比对即可。然后数组初始化。

void calc(ll id)//统计过根的路径 
{
	dis_vis[0]=1;//rt到自己的距离为0
	vector<ll> vt;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		cnt=0;//清空d数组 
		dis[y]=edge[i].l;
		get_dis(y,id);
		for(int j=1;j<=cnt;++j)
		{
			for(int k=1;k<=m;++k)
			{
				if(Q[k]>=d[j])
				{
					ans[k]|=dis_vis[Q[k]-d[j]];
				}
			}
		}
		for(int j=1;j<=cnt;++j) if(d[j]<=1e7) dis_vis[d[j]]=1,vt.push_back(d[j]);
	}
	for(auto j:vt) dis_vis[j]=0;//路径初始化 
}

最后是get_dis,也就是统计子树内的深度，同时记录一下深度，这个就很简单了

void get_dis(ll id,ll fa)
{
	d[++cnt]=dis[id];
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		dis[y]=edge[i].l+dis[id];
		get_dis(y,id);
	}
}

 注意我们的点分治都是在当前子树内进行，如果某一个点已经分治处理过了，我们直接跳过

完整代码

#include<bits/stdc++.h>
using namespace std;
#define ll int
#define IL inline
#define endl '\n'
const ll N=1e4+10;
namespace FastIOT{
	const int bsz=1<<18;
	char bf[bsz],*hed,*tail;
	inline char gc(){if(hed==tail)tail=(hed=bf)+fread(bf,1,bsz,stdin);if(hed==tail)return 0;return *hed++;}
	template<typename T>IL void read(T &x){T f=1;x=0;char c=gc();for(;c>'9'||c<'0';c=gc())if(c=='-')f=-1;
	for(;c<='9'&&c>='0';c=gc())x=(x<<3)+(x<<1)+(c^48);x*=f;}
	template<typename T>IL void print(T x){if(x<0)putchar(45),x=-x;if(x>9)print(x/10);putchar(x%10+48);}
	template<typename T>IL void println(T x){print(x);putchar('\n');}
}
using namespace FastIOT;
struct ty
{
	ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
void add(ll a,ll b,ll c)
{
	edge[++cn].t=b;
	edge[cn].l=c;
	edge[cn].next=head[a];
	head[a]=cn;
}
ll n,m;
ll a,b,c;
ll Q[110],siz[N],dis[N],mx[N],rt,nt;
//Q 询问 siz子树大小 dis到根的距离 mx最大子树对应节点 
ll cnt,d[N];//当前存在的路径长度 
bool vis[N],dis_vis[10000005];
//节点是否已经分治过，在某次分治中距离为dis_vis[i]的节点是否存在 
ll ans[110];
void find_rt(ll id,ll fa)
{
	siz[id]=1;mx[id]=0;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		find_rt(y,id);
		mx[id]=max(mx[id],siz[y]);
		siz[id]+=siz[y];
	} 
	mx[id]=max(mx[id],nt-siz[id]);//这里是nt-siz[id],因为重心要在不同子树里面求 
	if(mx[id]<mx[rt])
	{
		rt=id;
	}
}
void get_dis(ll id,ll fa)
{
	d[++cnt]=dis[id];
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		dis[y]=edge[i].l+dis[id];
		get_dis(y,id);
	}
}

void calc(ll id)//统计过根的路径 
{
	dis_vis[0]=1;//rt到自己的距离为0
	vector<ll> vt;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		cnt=0;//清空d数组 
		dis[y]=edge[i].l;
		get_dis(y,id);
		for(int j=1;j<=cnt;++j)
		{
			for(int k=1;k<=m;++k)
			{
				if(Q[k]>=d[j])
				{
					ans[k]|=dis_vis[Q[k]-d[j]];
				}
			}
		}
		for(int j=1;j<=cnt;++j) if(d[j]<=1e7) dis_vis[d[j]]=1,vt.push_back(d[j]);
	}
	for(auto j:vt) dis_vis[j]=0;//路径初始化 
}
void dfz_(ll id)//点分治 
{
	calc(id);
	vis[id]=1;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		//递归 
		rt=0;mx[rt]=nt=siz[y];
		find_rt(y,0);find_rt(rt,0);//更新siz
		dfz_(rt); 
	}
}
void solve()
{
	memset(head,-1,sizeof head);
	read(n);read(m);
	for(int i=1;i<n;++i)
	{
		read(a);read(b);read(c);
		add(a,b,c);
		add(b,a,c);
	}
	for(int i=1;i<=m;++i) read(Q[i]);
	mx[0]=nt=n;
	find_rt(1,0);
	find_rt(rt,0);//更新siz数组，因为现在是以一个新的点为根节点
	dfz_(rt); 
	for(int i=1;i<=m;++i)
	{
		cout<<(ans[i]?"AYE":"NAY")<<endl;
	}
}
int main()
{
	//ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	solve();
	return 0;
}

再来一道

聪聪可可

大意：

统计树上路径长%3=0的有序点对数

思路：

可以直接做树上dp，但是我们还是先来看一下点分治。跟上一题其实差不多，只不过我们需要统计数量罢了，那么只要在get_dis的时候，记录一下数量，对于之前子树的路径信息也记录一下数量，然后相乘再乘2就可以了（有序）

当然上面的计算不会包括根节点到自己的路径，因为我们都是在除根节点的子树内统计，所以最后ans还要+n

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=2e4+10;
struct ty
{
	ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
void add(ll a,ll b,ll c)
{
	edge[++cn].t=b;
	edge[cn].l=c;
	edge[cn].next=head[a];
	head[a]=cn;
}
ll n,m,a,b,c;
ll nc;//当前子树的大小
ll siz[N],mx[N];
ll rt;
ll vis[N],dis_vis[5];
ll cnt,dis[N],d[5];
//d:路径长为d[i]的点数 
ll ans;
void get_rt(ll id,ll fa)
{
	siz[id]=1;
	mx[id]=0;//最大子树初始化！ 
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		get_rt(y,id);
		siz[id]+=siz[y];
		mx[id]=max(mx[id],siz[y]);
	}
	mx[id]=max(mx[id],nc-mx[id]);
	if(mx[id]<mx[rt])
	{
		rt=id;
	}
}
void get_dis(ll id,ll fa)
{
	d[dis[id]]++;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		dis[y]=(edge[i].l+dis[id])%3;
		get_dis(y,id);	
	}	
} 
void calc(ll id)
{
	dis_vis[0]=1;//到自己的路径长
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		for(int i=0;i<=3;++i) d[i]=0;
		dis[y]=edge[i].l;
		get_dis(y,id);
		for(int i=0;i<3;++i)
		{
			ans+=2*dis_vis[i]*d[(3-i)%3];	
			dis_vis[i]+=d[i];
		} 
	} 
	//ans+=d[0]*d[0]+d[1]*d[2]*2;
	for(int i=0;i<=3;++i) dis_vis[i]=0;
}
void dfz_(ll id)
{
	calc(id);//统计过根的路径长&数量 
	vis[id]=1;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		rt=0;
		nc=mx[rt]=siz[y];
		get_rt(y,0);get_rt(rt,0);
		dfz_(rt);
	} 
}
void solve()
{
	memset(head,-1,sizeof head);
	cin>>n;
	for(int i=1;i<n;++i)
	{
		cin>>a>>b>>c;
		add(a,b,c%3);
		add(b,a,c%3);
	}
//	for(int i=1;i<=m;++i) cin>>Q[i];
	nc=mx[0]=n;
	get_rt(1,0);
	get_rt(rt,0);
	dfz_(rt);
	ans+=n;
	ll fm=n*n;
	ll g=__gcd(ans,fm);
	cout<<ans/g<<'/'<<fm/g<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	solve();
	return 0; 
}

考虑树上dp

我们记dp[i][j]表示以i为根的子树内有多少路径长%3=j的点对。转移的时候只要加上路径信息就可以了。统计的话，其实跟点分治在处理过根路径的时候一样。一个子树一个子树去搜索的话，对于某一个值j，dp[i][j]记录的一定是之前子树的信息（如果我们有更新），那么我们直接乘一下就好了（再*2），最后+n同理。因为规模不大，路径长也不大，所以这里我们是很好维护的，否则就只能用点分治了。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define IL inline
#define endl '\n'
const ll N=2e4+10;
namespace FastIOT{
	const int bsz=1<<18;
	char bf[bsz],*hed,*tail;
	inline char gc(){if(hed==tail)tail=(hed=bf)+fread(bf,1,bsz,stdin);if(hed==tail)return 0;return *hed++;}
	template<typename T>IL void read(T &x){T f=1;x=0;char c=gc();for(;c>'9'||c<'0';c=gc())if(c=='-')f=-1;
	for(;c<='9'&&c>='0';c=gc())x=(x<<3)+(x<<1)+(c^48);x*=f;}
	template<typename T>IL void print(T x){if(x<0)putchar(45),x=-x;if(x>9)print(x/10);putchar(x%10+48);}
	template<typename T>IL void println(T x){print(x);putchar('\n');}
}
using namespace FastIOT;
struct ty
{
	ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
void add(ll a,ll b,ll c)
{
	edge[++cn].t=b;
	edge[cn].l=c;
	edge[cn].next=head[a];
	head[a]=cn;
}
ll n,m;
ll a,b,c;
ll dp[N][5];
ll ans=0;
void dfs(ll id,ll fa)
{
	dp[id][0]=1;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa) continue;
		dfs(y,id);
		for(int j=0;j<3;++j)
		{
			ans+=dp[id][j]*dp[y][((-j-edge[i].l)%3+3)%3]*2;
		}
		for(int j=0;j<3;++j)
		{
			dp[id][(j+edge[i].l)%3]+=dp[y][j];
		}
	}
} 
void solve() 
{
	memset(head,-1,sizeof head);
	cin>>n;
	for(int i=1;i<n;++i)
	{
		cin>>a>>b>>c;
		add(a,b,c%3);
		add(b,a,c%3);
	} 
	dfs(1,0);
	ans+=n;
	ll fm=n*n;
	ll g=__gcd(fm,ans);
	ans/=g;fm/=g;
	cout<<ans<<"/"<<fm<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	solve();
	return 0;
}

再来一道

Distance in Tree

统计树上路径长为k的数量。

这算是前两个的小综合了。思路差不多，自己试试

#include<bits/stdc++.h>
using namespace std;
#define ll int
#define IL inline
#define endl '\n'
const ll N=5e4+10;
namespace FastIOT{
	const int bsz=1<<18;
	char bf[bsz],*hed,*tail;
	inline char gc(){if(hed==tail)tail=(hed=bf)+fread(bf,1,bsz,stdin);if(hed==tail)return 0;return *hed++;}
	template<typename T>IL void read(T &x){T f=1;x=0;char c=gc();for(;c>'9'||c<'0';c=gc())if(c=='-')f=-1;
	for(;c<='9'&&c>='0';c=gc())x=(x<<3)+(x<<1)+(c^48);x*=f;}
	template<typename T>IL void print(T x){if(x<0)putchar(45),x=-x;if(x>9)print(x/10);putchar(x%10+48);}
	template<typename T>IL void println(T x){print(x);putchar('\n');}
}
using namespace FastIOT;
struct ty
{
	ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
void add(ll a,ll b,ll c)
{
	edge[++cn].t=b;
	edge[cn].l=c;
	edge[cn].next=head[a];
	head[a]=cn;
}
ll n,m;
ll a,b,c;
ll siz[N],dis[N],mx[N],rt,nt;
//dis到根的距离 mx最大子树对应节点 
ll cnt;//当前存在的路径长度 
ll vis[N],dis_vis[N];
//节点是否已经分治过，在某次分治中距离为dis_vis[i]的节点是否存在 
ll ans;
map<ll,ll> mp;
void find_rt(ll id,ll fa)
{
	siz[id]=1;mx[id]=0;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		find_rt(y,id);
		mx[id]=max(mx[id],siz[y]);
		siz[id]+=siz[y];
	} 
	mx[id]=max(mx[id],nt-siz[id]);//这里是nt-siz[id],因为重心要在不同子树里面求 
	if(mx[id]<mx[rt])
	{
		rt=id;
	}
}
void get_dis(ll id,ll fa)
{
	mp[dis[id]]++;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(y==fa||vis[y]) continue;
		dis[y]=edge[i].l+dis[id];
		get_dis(y,id);
	}
}

void calc(ll id)//统计过根的路径 
{
	dis_vis[0]=1;//rt到自己的距离为0
	vector<ll> vt;
	
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		dis[y]=edge[i].l;
		mp.clear();
		get_dis(y,id);
		for(auto j:mp)
		{
			if(m<j.first) continue;
			ans+=dis_vis[m-j.first]*j.second;
		}
		for(auto j:mp)
		{
			if(m<j.first) continue;
			dis_vis[j.first]+=j.second;
			vt.push_back(j.first);
		}
	}
	for(auto j:vt) dis_vis[j]=0;//路径初始化 
	
}
void dfz_(ll id)//点分治 
{
	calc(id);
	vis[id]=1;
	for(int i=head[id];i!=-1;i=edge[i].next)
	{
		ll y=edge[i].t;
		if(vis[y]) continue;
		//递归 
		rt=0;mx[rt]=nt=siz[y];
		find_rt(y,0);find_rt(rt,0);//更新siz
		dfz_(rt); 
	}
}
void solve()
{
	memset(head,-1,sizeof head);
	read(n);read(m);
	for(int i=1;i<n;++i)
	{
		read(a);read(b);
		add(a,b,1);
		add(b,a,1);
	}
	mx[0]=nt=n;
	find_rt(1,0);
	find_rt(rt,0);//更新siz数组，因为现在是以一个新的点为根节点
	dfz_(rt); 
	printf("%lld\n",ans);
}
int main()
{
	//ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	solve();
	return 0;
}

未完待续~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/195949.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【手撕面试题】HTML+CSS（高频知识点二）

【手撕面试题】HTML+CSS（高频知识点二）

目录 面试官&#xff1a;页面导入样式时&#xff0c;使用 link 和 import 有什么区别&#xff1f; 面试官&#xff1a;简要说说 title与h1的区别、b与strong的区别、i与em的区别&#xff1f; 面试官&#xff1a;img标签的title和alt有什么区别&#xff1f; 面试官&#xff…
阅读更多...
给特别规则FeignClient增加统一的RequestInterceptor

给特别规则FeignClient增加统一的RequestInterceptor

需求背景&#xff1a; 在微服务横行天下的今天&#xff0c;Spring Cloud OpenFeign 早就成了我们服务间调度的主要远程调用手段。 在Feign进行远程调度的时候&#xff0c;难免会做一些心跳&#xff0c;权限的校验&#xff0c;来保证调度过程的相对安全。 但对于外部系统来说…
阅读更多...
Unity 之 Addressable可寻址系统 -- 资源远程加载 | 资源预下载 -- 进阶（三）

Unity 之 Addressable可寻址系统 -- 资源远程加载 | 资源预下载 -- 进阶（三）

可寻址系统远程加载 -- 资源预下载 -- 进阶&#xff08;三&#xff09;一&#xff0c;Unity 云资源分发 -- 使用介绍1.1 CCD 的介绍1.2 后台准备工作二&#xff0c;CDD的使用2.1 CCD可视化界面的使用2.2 CDD命令行界面使用2.2.1 准备工作2.2.2 CLI 用法三&#xff0c;AA CCD资…
阅读更多...
Java中的快速排序

Java中的快速排序

快速排序递归版本挖坑法Hoare法优化非递归相信即使大家并不知道快速排序究竟是个啥,但也一定听说过快排,今天我来给兄弟们讲讲快速排序!递归版本 快速排序的思想就是找基准,就比如我们以数组中的第一个数字12为基准,我们从最后往前面找,如果找到一个比12小的数字就用它覆盖12,但…
阅读更多...
Linux—InstallOS-RedHat9.1

Linux—InstallOS-RedHat9.1

下载https://developers.redhat.com/products/rhel/download 需注册账号。安装正常安装就行。安装注意事项&#xff1a;(1)Software SelectionCentOS的摘录过来&#xff0c;通用。最小安装&#xff08;Minimal Install&#xff09;这个选项只提供运行CentOS 的基本软件包。最小…
阅读更多...
Python学习-----起步4（列表元素的添加，删除，修改，查询，获取长度）

Python学习-----起步4（列表元素的添加，删除，修改，查询，获取长度）

目录 前言&#xff1a; 列表元素的添加&#xff08;或者叫写入&#xff09; 1.append&#xff08;&#xff09;函数 2.extend&#xff08;&#xff09;函数 3.insert()函数 列表元素的删除 1.remove() 函数 2. pop() 函数 3.clear&#xff08;&#xff09;函数 4.del …
阅读更多...
公司40岁的程序員到底在写什么代码

公司40岁的程序員到底在写什么代码

去年在前公司玩了一年&#xff08;基本兩三個月一個需求&#xff09;&#xff0c;除了日常維護就一些特別簡單的功能開發&#xff0c;到年底也沒見到公司黃&#xff08;國企背景&#xff09;&#xff0c;沒辦法只好裸辭&#xff0c;現在這個公司各方面还不错&#xff0c;但是令…
阅读更多...
Cookie、Session、Token、JWT只看这一篇文章就够了

Cookie、Session、Token、JWT只看这一篇文章就够了

什么是认证&#xff08;Authentication&#xff09; 通俗地讲就是验证当前用户的身份&#xff0c;证明“你是你自己”&#xff08;比如&#xff1a;你每天上下班打卡&#xff0c;都需要通过指纹打卡&#xff0c;当你的指纹和系统里录入的指纹相匹配时&#xff0c;就打卡成功&a…
阅读更多...
MongoDB Map Reduce

MongoDB Map Reduce

在用 MongoDB 查询时&#xff0c;若返回的数据量很大&#xff0c;或者做一些比较复杂的统计和聚合操作做花费的时间很长时&#xff0c;可以使用 MongoDB 中的 mapReduce 进行实现。mapReduce 是个灵活且强大的数据聚合工具&#xff0c;它的好处是可以把一个聚合任务分解为多个小…
阅读更多...
设计模式(三)----创建型模式之单例模式（一）

设计模式(三)----创建型模式之单例模式（一）

一、创建型模式 创建型模式的主要关注点是“怎样创建对象&#xff1f;”&#xff0c;它的主要特点是“将对象的创建与使用分离”。 这样可以降低系统的耦合度&#xff0c;使用者不需要关注对象的创建细节。 创建型模式分为&#xff1a; 单例模式 工厂方法模式 抽象工厂模式…
阅读更多...
英语学习 3

英语学习 3

1 词汇积累 1、ships 船 2、class 级 3、marvels 奇迹 4、marvelous 非凡的、了不起的、极好的 5、cursed 诅咒、被诅咒的 6、the most luxurious ships 最豪华的船 7、luxury 奢侈、奢华的 8、luxurious 心满意足的、舒适的 9、utmost 极度的、最大的 10、kind 种类 11、voya…
阅读更多...
Kali Linux神秘工具教程(详细版)

Kali Linux神秘工具教程(详细版)

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录前言一、Kali Linux - 安装和配置信息收集工具二、NMAP隐形扫描搜索Searchsploit域名系统工具dnsenum.plDNSMAPdnstracerLBDHping3漏洞分析工具Cisco-torch工具Cisco…
阅读更多...
回溯算法（基础）

回溯算法（基础）

目录 一、基本概念 二、以简单全排列认识回溯 &#xff08;一&#xff09;决策树 &#xff08;二&#xff09;回溯示意图 &#xff08;三&#xff09;核心代码 &#xff08;四&#xff09;完整代码 三、组合问题 &#xff08;一&#xff09;问题 &#xff08…
阅读更多...
如何通过groovy扩展方法

如何通过groovy扩展方法

最近一直使用jmeter做接口测试&#xff0c;虽然好用&#xff0c;但是每次解析结果都要写大量重复代码。然后想到groovy是可以在运行时动态增强jvm字节码的&#xff0c;比如Date中就有大量增强的方法&#xff0c;比如format,upto,downto......&#xff0c;既然groovy可以&#x…
阅读更多...
用 NFTScan 的角度解析 Yuga labs NFT 项目系列

用 NFTScan 的角度解析 Yuga labs NFT 项目系列

如果要说 NFT 影响力最大的公司是哪个&#xff1f;如果说是 Yuga Labs 应该我想大家应该都不会否认。一个创立一年多的 NFT 营销和开发公司&#xff0c;多次的并购以及行销操作都立下 NFT 界的标竿典范&#xff0c;尤其 BAYC NFT 系列取得巨大成功之后&#xff0c;该团队已成为…
阅读更多...
DSP_定义一个大的全局数组_探索之路

DSP_定义一个大的全局数组_探索之路

前言 最近在做基于dsp平台的无通信接口系统辨识&#xff0c;辨识的时候会有很大的数据需要存到一个数组当中&#xff0c;而dsp如果定义一个很大的全局数组&#xff0c;编译会报错。 本文将探索如何解决这个报错以及全局数组的大小极限。 正文 首先&#xff0c;我们定义了一个…
阅读更多...
数学库:Extreme Optimization Numerical 8.1.4 Crack

数学库:Extreme Optimization Numerical 8.1.4 Crack

Extreme Optimization Numerical.NET 的极端优化数值库&#xff0c;更快地构建金融、工程和科学应用程序&#xff0c;具有置信度和预测带的非线性曲线拟合&#xff0c;用于 .NET的极端优化数值库是为 Microsoft .NET 框架构建的通用数学和统计类的集合。用于 .NET的极端优化数值…
阅读更多...
将无风险资产与单个风险资产进行组合

将无风险资产与单个风险资产进行组合

目录 1. 基本概念 2. 将无风险资产与单个风险资产进行组合 3. 有效资产组合 1. 基本概念 无风险资产和风险资产。 我的理解&#xff1a;无风险资产利率完全可确定&#xff0c;风险资产的利率称为预期收益率&#xff0c;并且有标准差。 关于风险资产预期收益率和标准差的计…
阅读更多...
NC65 自由报表发布为节点如何显示以及如何取消已发布的报表节点

NC65 自由报表发布为节点如何显示以及如何取消已发布的报表节点

NC65 自由报表发布为节点如何显示以及如何取消已发布的报表节点&#xff1f; 一、NC65 自由报表发布为节点如何显示&#xff1f; 答&#xff1a;需要在动态建模平台-权限管理-职责管理下的职责节点进行功能分配&#xff0c;如下图&#xff1a; 二、如何取消已发布的报表节…
阅读更多...
Javac Spire.Presentation 之PPT文本图片内容提取

Javac Spire.Presentation 之PPT文本图片内容提取

目录结构前言文档准备引入Maven依赖代码块提取结果验证ppt_demo.ppt 提取结果pptx_demo.pptx 提取结果前言 应公司需求&#xff0c;需实现以下功能 PPT文本内容的替换&#xff1b;PPT文本内容的提取&#xff1b;PPT中图片的提取存放&#xff1b; 此文章将使用Spire.Presenta…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023