目录
1. 基本概念
2. 将无风险资产与单个风险资产进行组合
3. 有效资产组合
1. 基本概念
无风险资产和风险资产。
我的理解:无风险资产利率完全可确定,风险资产的利率称为预期收益率,并且有标准差。
关于风险资产预期收益率和标准差的计算。
题、根据下表数据,计算股票 A 和 B 的相关系数。
| 经济状态 | 发生概率 | 股票 A 收益率 | 股票 B 收益率 |
| 中度衰退 | 0.05 | -0.02 | -0.20 |
| 轻度衰退 | 0.15 | -0.01 | -0.10 |
| 温和增长 | 0.60 | 0.15 | 0.15 |
| 较大增长 | 0.20 | 0.15 | 0.30 |
分析:A 和 B 显然是风险资产。首先根据概率论知识求期望和标准差。

再根据概率论知识求相关系数。

资产组合。
资产组合是指投资者资金配置在不同的资产上形成的资产组合。
资产组合的收益等于各资产收益的加总。
核心就是你在不同资产上投多少权重。
2. 将无风险资产与单个风险资产进行组合
步骤 1:将资产组合的预期收益率与投资于风险资产的比例相关联。

实质就是分配权重,总收益等于各资产收益的加权加总。上式可变形为:
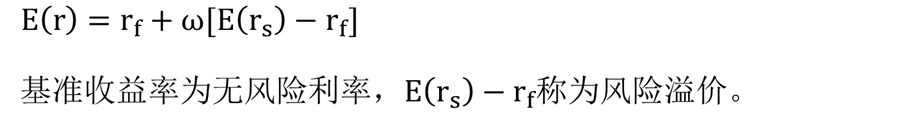
步骤 2:将资产组合的标准差与投资于风险资产的比例相关联。
由于无风险资产利率完全可确定,因此其标准差为 0 。故资产组合的标准差只与风险资产的标准差有关,等于风险资产的标准差乘以其权重。
![]()
步骤 3:将资产组合的预期收益率与其标准差相关联。

可见,资产组合的预期收益率与资产组合的标准差呈线性相关关系。
我们可以画出函数图像。
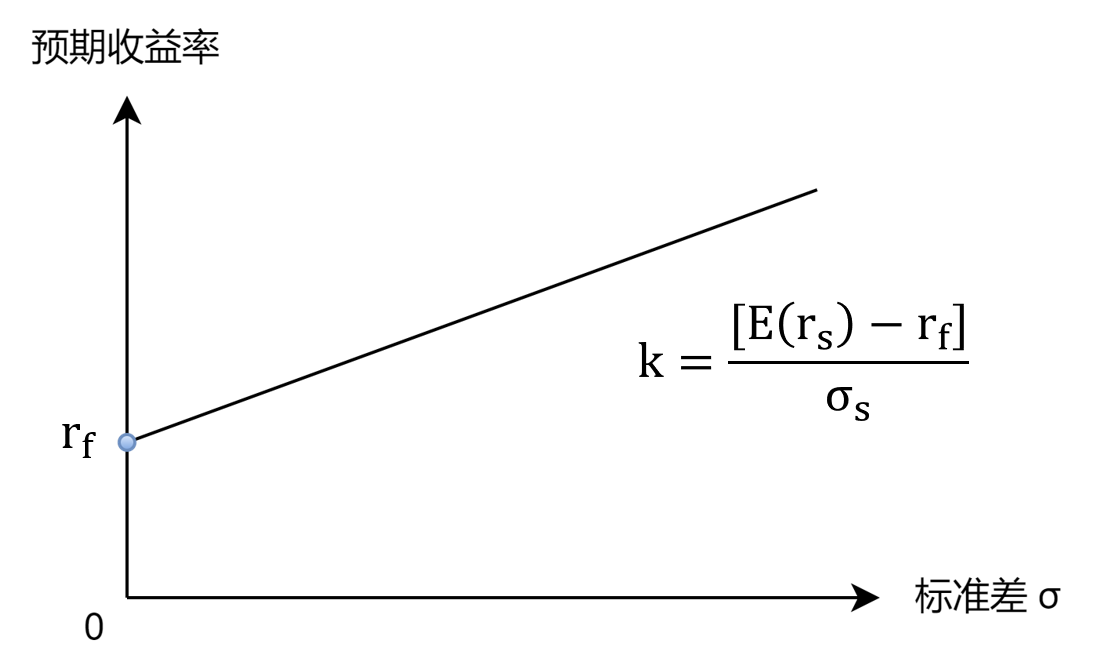
3. 有效资产组合
有效资产组合:是指在特定风险水平下向投资者提供最高可能预期收益率的资产组合。
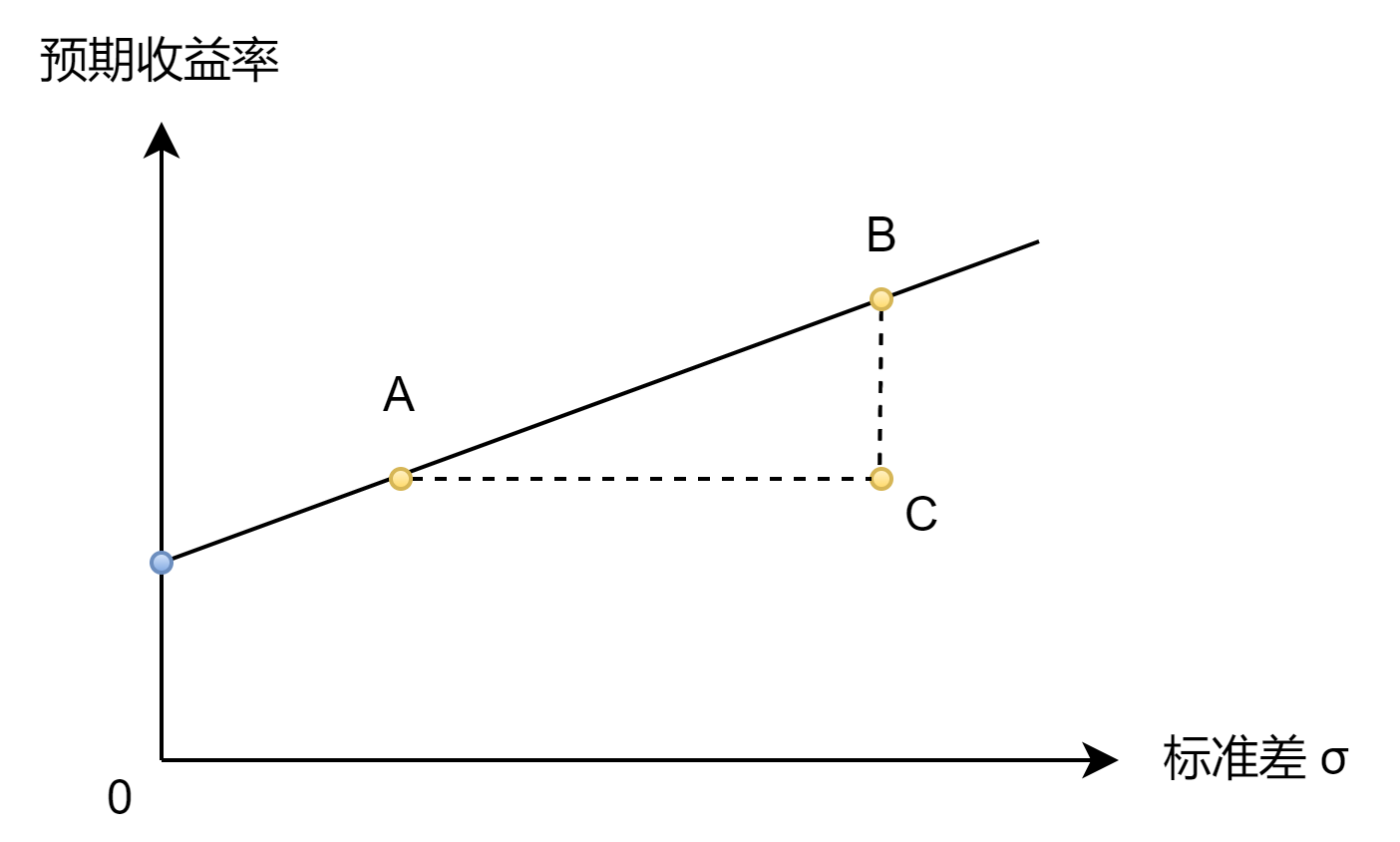
假设你是一个冤大头,你选择了资产组合 C 。相较于组合 A,组合 C 虽然与其预期收益率相同,但是具有更大的标准差;相较于组合 B,组合 C 虽然与其标准差相同,但是具有更低的预期收益率。实际上 AB 连线上的任一点都比 C 拥有更高的预期收益率,更小的标准差。总结:你是一个冤大头。
可以证明,直线上的每一点,即每一种资产组合,都能在特定风险水平下向投资者提供最高可能预期收益率。因此,它们均为有效资产组合。