文章目录
- diff
- ediff1d
diff
diff是numpy中用于求差分的函数,函数定义为
diff(a, n=1, axis=-1, prepend=<no value>, append=<no value>)
其中a为数组,n为差分的阶数,axis为求导对应的坐标轴,默认-1表示最后一个轴。
例如
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(100)/10
y = np.sin(x)
dy = np.diff(y)/0.1
ddy = np.diff(y, 2)/0.01
dddy = np.diff(y, 3)/0.001
plt.plot(y, label="y")
plt.plot(dy, label="dy")
plt.plot(ddy, label="ddy")
plt.plot(dddy, label="dddy")
plt.legend()
plt.show()
结果为

众所周知
sin
′
x
=
cos
x
,
sin
′
′
x
=
cos
′
x
=
−
sin
x
\sin'x=\cos x,\quad \sin''x=\cos'x=-\sin x
sin′x=cosx,sin′′x=cos′x=−sinx,所以上图中dy的曲线变成了cos的曲线。
但是
sin
′
x
=
d
y
d
x
\sin'x=\frac{\text dy}{\text dx}
sin′x=dxdy,而diff其实只表现出了dy的变化,是相邻连个值做减法而已。所以dy在diff之后,又除以dx。
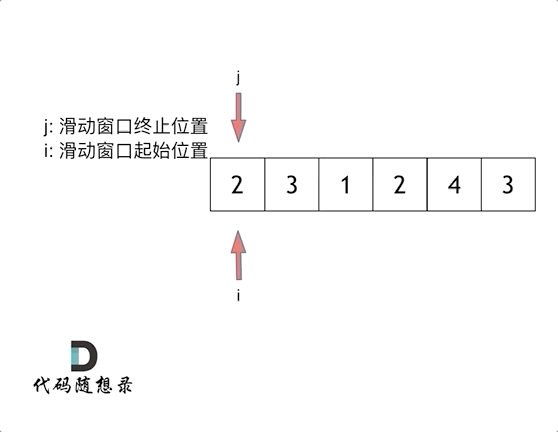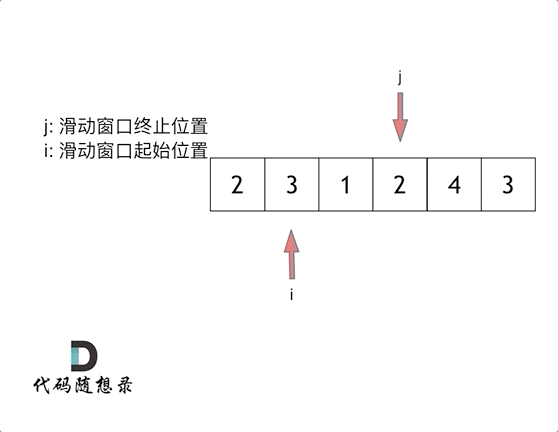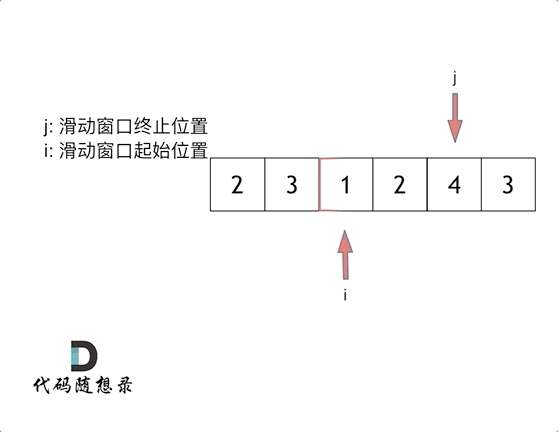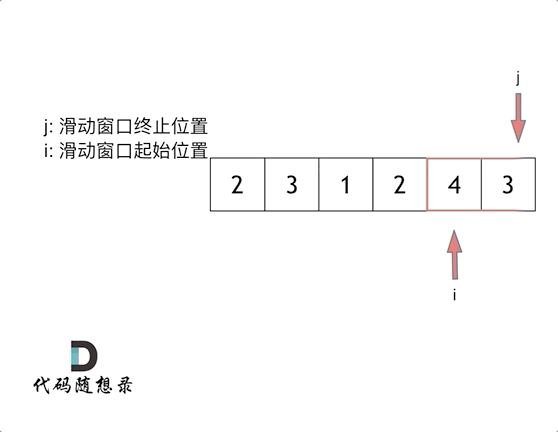
对于一个长度为n的数组而言,在进行1阶求导之后,长度必然会变成n-1,在某些情况下,若想对比导数与原函数的关系,那么这种长度的变化会导致绘图变得十分困难
>>> plt.plot(y, dy)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "D:\CS\Anaconda3\lib\site-packages\matplotlib\pyplot.py", line 2769, in plot
return gca().plot(
File "D:\CS\Anaconda3\lib\site-packages\matplotlib\axes\_axes.py", line 1632, in plot
lines = [*self._get_lines(*args, data=data, **kwargs)]
File "D:\CS\Anaconda3\lib\site-packages\matplotlib\axes\_base.py", line 312, in __call__
yield from self._plot_args(this, kwargs)
File "D:\CS\Anaconda3\lib\site-packages\matplotlib\axes\_base.py", line 498, in _plot_args
raise ValueError(f"x and y must have same first dimension, but "
ValueError: x and y must have same first dimension, but have shapes (100,) and (99,)
ediff1d
相比之下ediff1d尽管只能做一阶的差分计算,但提供了前后补全的功能,其定义为
numpy.ediff1d(ary, to_end=None, to_begin=None)
to_end和to_begin分别是在diff结果的后面和前面补充的数组。
x = np.arange(100)/10
y = np.sin(x)
dy = np.ediff1d(y, to_begin=0)/0.1
plt.plot(y, dy)
plt.show()
效果如下