前端算法之二分查找

news2024/11/17 6:47:36

在数组中查找指定元素,如果存在就返回它的位置,如果不存在,就返回-1。

这是一道非常经典的算法题，考的就是二分查找算法，首先分析二分查找的思路：

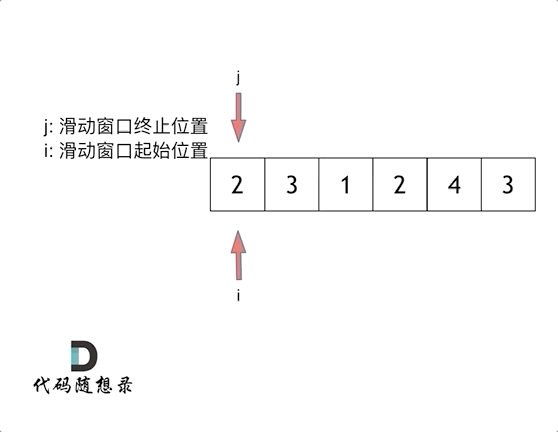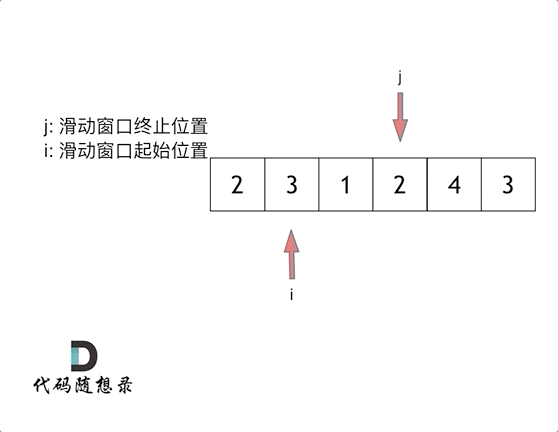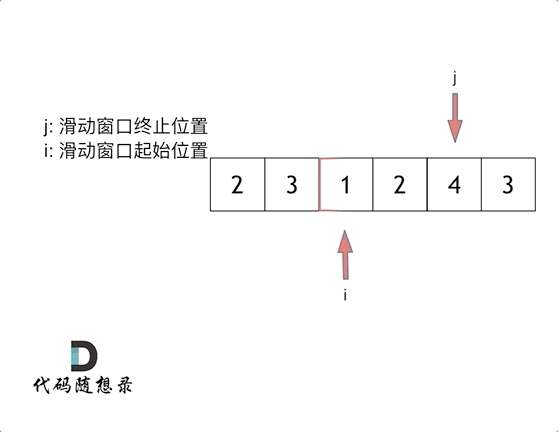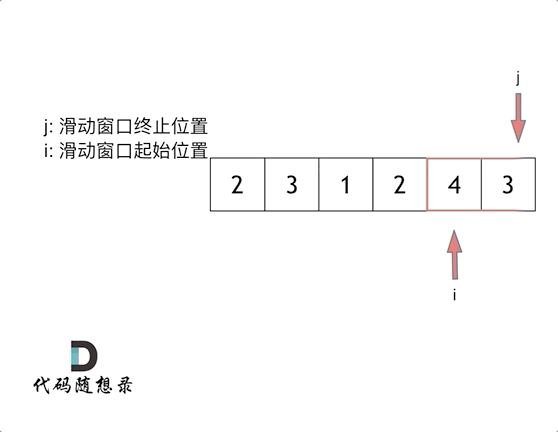
假设一个数组为 [3,5,19,22,25,33,45,47,57,66,71,78]（已经从小到大排好序），要求找出数值80的位置，如图：

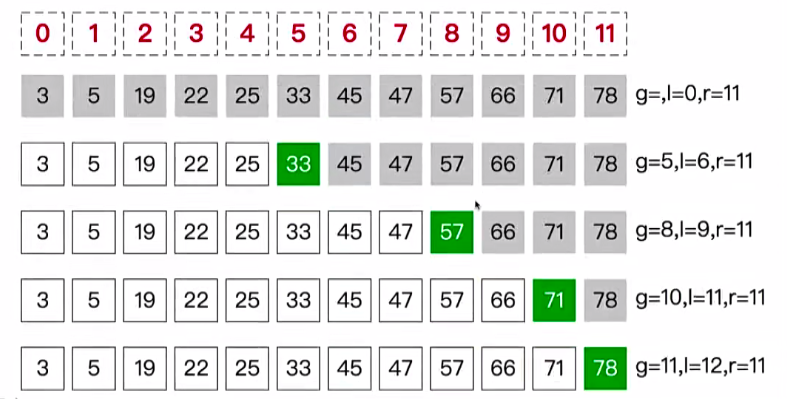
ps: g 为猜测数值的位置，l 为查找的起点，r 为查找的终点，灰色方格为查找范围

步骤：

　　1.刚开始查找范围为整个数组，第一次猜测数值是33，也就是猜测位置 g 为5，这个5是通过( l + r ) / 2 向下取整 得出的即（0 + 11）/ 2 = 5，由于当前数值为33，并不是目标数值80，且小于80，继续向右查找

　　2.第二次查找，起点 l 为上一次猜测位置的下一位，即 l = 5 +1 = 6，r 还是为11，此次猜测位置 g 为（ l + r ）/ 2 = 8，对应数值为57，也小于80，继续下一轮向右查找

　　3.第三次查找，起点 l 为上次猜测位置的下一位，即 l = 8 + 1 = 9，r 还是为11，此次猜测位置 g 为（ l + r ）/ 2 = 10，对应数值为71，也小于80，继续下一轮向右查找

　　4.第四次查找，起点 l 为上次猜测位置的下一位，即 l = 10 + 1 = 11，r 还是为11，此次猜测位置 g 为（ l + r ）/ 2 = 11，对应数值为78，也小于80，继续下一轮向右查找

　　5.第五次查找，起点 l 为上次猜测位置的下一位，即 l = 11 + 1 = 12，r 还是为11，此时 l > r ,查找终止，且未找到目标数值，由于未找到80，所以应当返回-1。

其他条件不变，将目标值换成66，利用二分查找找出对应数值的位置，如图：

步骤：

　　1.刚开始查找范围为整个数组，第一次猜测数值是33，也就是猜测位置 g 为5，这个5是通过( l + r ) / 2 向下取整 得出的即（0 + 11）/ 2 = 5，由于当前数值为33，并不是目标数值66，且小于66，继续向右查找

　　2.第二次查找，起点 l 为上一次猜测位置的下一位，即 l = 5 + 1 = 6，r 还是为11，此次猜测位置 g 为（ l + r ）/ 2 = 8，对应数值为57，也小于66，继续下一轮向右查找

　　3.第三次查找，起点 l 为上次猜测位置的下一位，即 l = 8 + 1 = 9，r 还是为11，此次猜测位置 g 为（ l + r ）/ 2 = 10，对应数值为71，由于71大于目标数值66，因此下一轮需向左查找

　　4.第四次查找，起点 l 不变，即 l = 9，r 为上次猜测位置 g 的上一位即9，由于 l 和 r 相同，所以该位置的数值为最后一个需要查找的数值，不需要继续猜测查找了，而该数值也正好为目标数值66，因此返回目标数值66的位置为9。

通过以上分析，下面看看具体代码实现：

function bsearch(A, x) {
    let l = 0, // 查询范围左边界
      r = A.length - 1, // 查询范围右边界
      g; // 猜测位置，即l,r中间的位置
    while (l <= r) {
      g = Math.floor((l + r) / 2); // 向下取整
      // 循环不变式
      if (A[g] === x) return g;
      else if (A[g] > x) r = g - 1;
      else l = g + 1;
    }
    return -1;
  }

测试结果：

ps：递归二分查找

function bsearch1(A, x, l = 0, r = A.length - 1, g) {
    if (l <= r) {
      g = Math.floor((l + r) / 2);
      if (A[g] === x) return g;
      else if (A[g] > x) r = g - 1;
      else l = g + 1;
      return bsearch1(A, x, l, r, g);
    }
    return -1;
  }

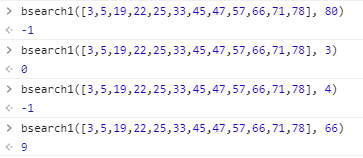
测试结果：