977.有序数组的平方

力扣题目链接

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1： 输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

示例 2： 输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

对于上述指针其实是有序的，只不过有可能负数平方后大于正数

所以可以得出一个结论，最大值总是在两边的。

这个时候就可以考虑使用双指针，i指向起始位置，j指向终止位置

然后定义一个新的数组，因为要排序，介于使用双指针每次找到的都是最大的，所以对于新数组的下标要从最后一个位置来进行存储，所以新数组的长度要和原数组一样。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* sortedSquares(int* nums, int numsSize, int* returnSize){
    *returnSize = numsSize;//这里其实不是很理解，搜的解释如其实就是需要对return的数组的长度进行限定，尝试了下面的代码，输出结果相同。但是*returnSize = numsSize;具有其动态意义，可以根据输入的数组长度直接生成return的长度。
    int left = 0; //指向最左边
    int right = numsSize-1;//指向最右边
    int *ans = (int *)malloc(sizeof(int)* numsSize);//创建一个新数组，长度和原数组一样
    int index;//新数组的下标
    for(index = numsSize - 1; index >= 0; index--)//新数组从最后面的位置进行赋值，因为，数组存储是从0开始的，所以最后一个位置是数组的长度减1，
    {
        int l = nums[left] * nums[left];//计算左侧的平方
        int r = nums[right] * nums[right];//计算右侧的平方
        if(l > r)//对得到的值进行比较，实际有三种可能，但是因为相等的话谁放在最后都可以，所以就可以分两种情况
        {
            ans[index] = l;//若左边的平方大于右边，让新数组等于左边的平方
            left++;//因为左边已经放入新数组一个值了，所以需要前进一个指向数组下一个位置
        }
        else//同上
        {
            ans[index] = r;
            right--;
        }
    }
    return ans;//最后返回新数组就可以了
}

209.长度最小的子数组

力扣题目链接

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

这道题的思路，滑动窗口，就是不断调整子序列的起始和终止位置，从而得到我们想要的结果

使用双指针来完成这个题目

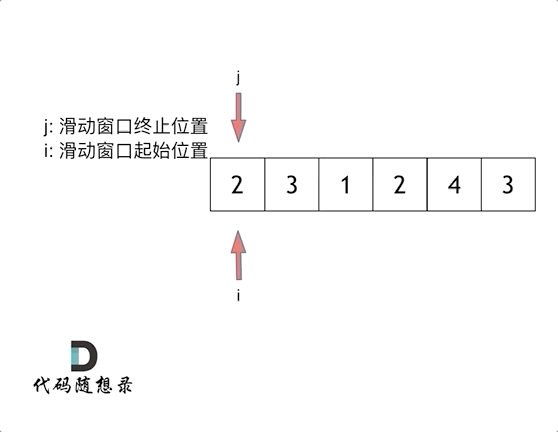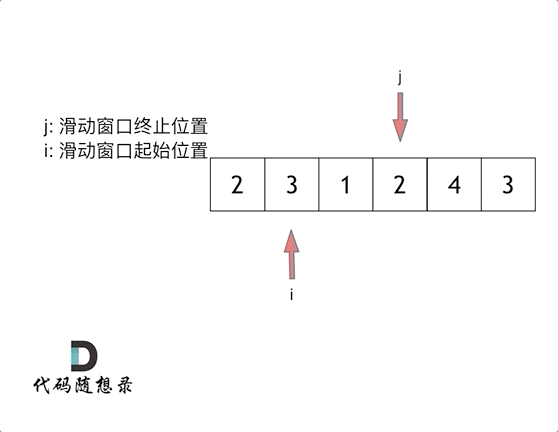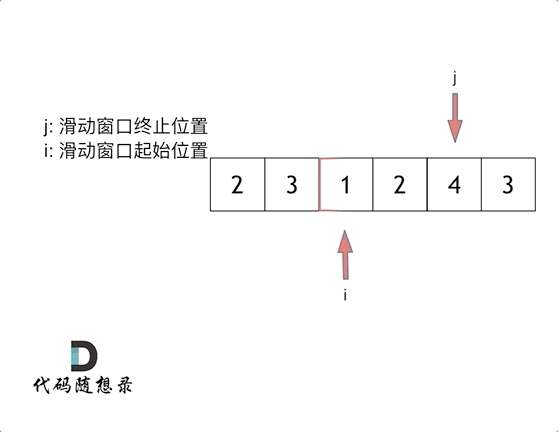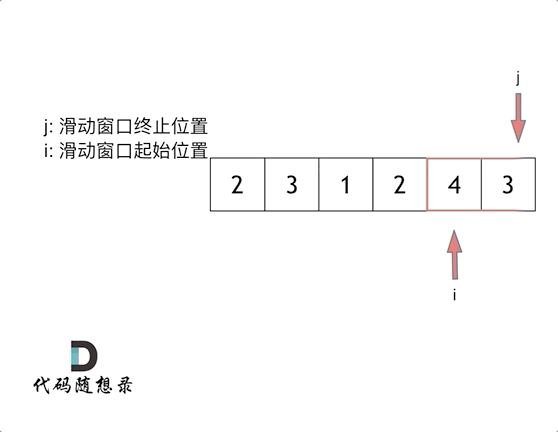
最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

• 窗口内是什么？

• 如何移动窗口的起始位置？

• 如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

快慢指针，i慢指针，j快指针，

移动的条件

i的值加j的值，如果小于s的值，则j移动

如果i加j大于或等于s，i移动用来缩小，直到遍历完

遍历的时候需要一个值来保存i到j的长度，最后来返回

int minSubArrayLen(int target, int* nums, int numsSize){
    int min = INT_MAX;//定义最小值为最大值
    int sum = 0;//定义和初始为0

    int i = 0;//慢指针
    int j = 0;//快指针
    for( ; j < numsSize ; j++ )//根据快指针的移动退出循环
    {
        sum += nums[j];//开始的时候sum的值为第一个，后续当sum<目标值的时候，j移动然后和再叠加
        while(sum >= target)//一旦当sum>=目标值的时候，就需要移动慢指针i了，并且记录下i到j的距离，并和min作比较，保存最短的距离
        {
            int length = j - i + 1; //实际长度是数组下标+1
            min = min < length ? min : length; //判断每次更新的长度是不是最短的
            sum= sum - nums[i];//判断完后，需要和减去i位置的值
            i++;//i向后移动一个距离
        }
    }

    return min == INT_MAX ? 0 :min;
    
}

59.螺旋矩阵II

---

力扣题目链接

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
    //初始化返回的结果数组的大小
    *returnSize = n;
    *returnColumnSizes = (int *)malloc(sizeof(int) * n);
    //初始化返回结果数组ans
    int **ans = (int **)malloc(sizeof(int *) *n);
    int i;
    for(i = 0; i <n ;i ++)
    {
        ans[i] = (int *)malloc(sizeof(int ) *n );
        (*returnColumnSizes)[i] = n;

    }
    //设置每次循环的起始位置
    int startx = 0;
    int starty = 0;
    //设置二维数组的中间值，若n为奇数，需要在最后中间填入数字
    int mid = n / 2;
    //循环圈数
    int loop = n / 2;
    //偏移数
    int offset = 1;
    //当前要添加的元素
    int count = 1;
    while(loop)
    {
        int i = startx;
        int j = starty;
        //模拟上侧从左到右
        for(; j < starty + n - offset; j++)
        {
            ans[startx][j] = count++;
        }
         //模拟右侧从上到下
        for(; i < startx + n - offset; i++)
        {
            ans[i][j] = count++;
        }
         //模拟下侧从右到左
        for(; j > starty ; j--)
        {
            ans[i][j] = count++;
        }
           //模拟左侧从下到上
        for(; i > startx ; i--)
        {
            ans[i][j] = count++;
        }
         //偏移值每次加2
        offset+=2;
        //遍历起始位置每次+1
        startx++;
        starty++;
        loop--;
    }
    //若n为奇数需要单独给矩阵中间赋值
    if(n%2)
    ans[mid][mid] = count;

    return ans;



}
控制台