目录

序言：

🏆🏆人生在世，成功并非易事，他需要破茧而出的决心，他需要永不放弃的信念，他需要水滴石穿的坚持，他需要自强不息的勇气，他需要无畏无惧的凛然。要想成功，你得付出沉重的代价。

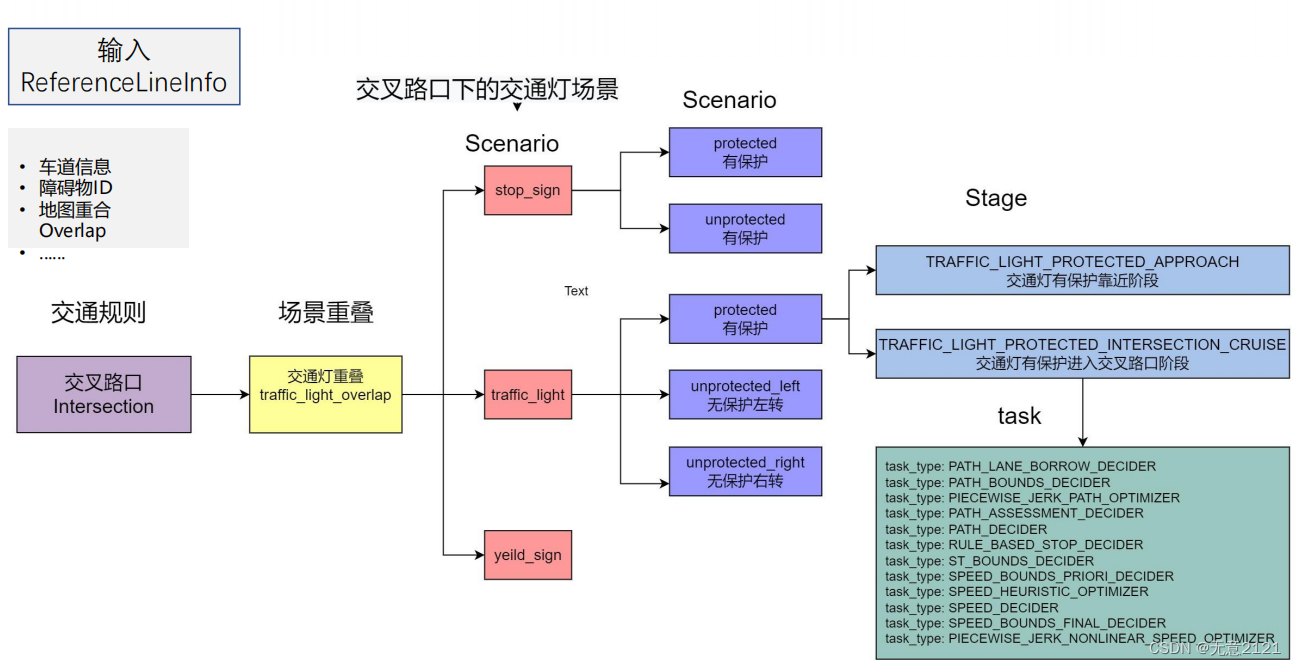
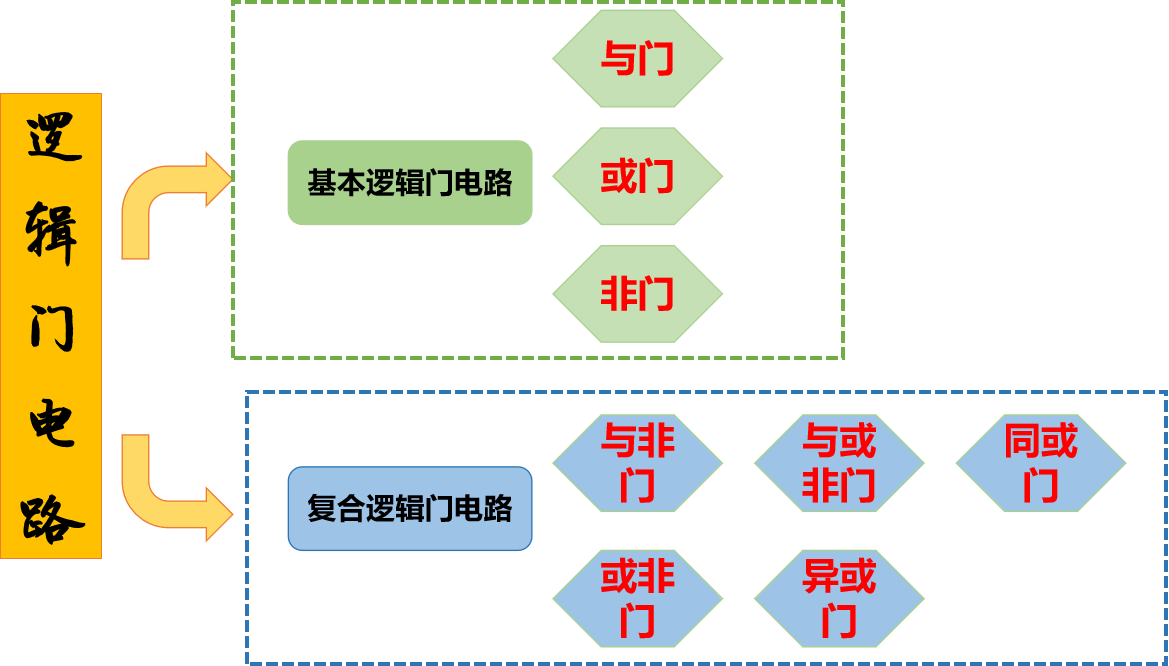
🍇一、逻辑门电路的分类 

🍇二、基本逻辑门电路

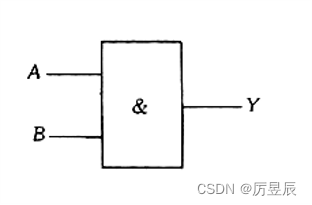
（1）与门电路

①图形符号

 ②表达式

③二极管及电阻组成的与门电路及分析

 （2）或门电路

①图形符号

②表达式

③二极管及电阻组成的或门电路及分析

（3）非门电路

①图形符号

②表达式 

③三极管及电阻组成的非门电路及分析

🍇三、复合逻辑门电路

（1）与非电路【有0出1，全1出0】

①图形符号

②表达式

③真值表

 （2）或非电路【有1出0，全0出1】

①图形符号

②表达式

③真值表

 （3）异或电路【相异出1】

①图形符号

②表达式

③真值表

 （4）同或电路【相同出1】

①图形符号

②表达式

③真值表

 （5）与或非电路

①图形符号

②表达式

🍇四、集成逻辑门电路

（1）TTL集成逻辑门电路

①型号及意义

②引脚的识读

TTL集成电路的特点

（2）CMOS集成逻辑门电路

①型号及意义

 ②种类

CMOS集成电路的特点

---

序言：

本文章仅粉丝可见，望谅解🙏🙏

从本篇文章开始就进行电子笔记的一个汇总，属于个人的权限文章，所以设置为粉丝可见，再次望谅解🙏🙏

---

🏆🏆人生在世，成功并非易事，他需要破茧而出的决心，他需要永不放弃的信念，他需要水滴石穿的坚持，他需要自强不息的勇气，他需要无畏无惧的凛然。要想成功，你得付出沉重的代价。

---

 

一、逻辑门电路的分类 

二、基本逻辑门电路

（1）与门电路

①图形符号

 ②表达式

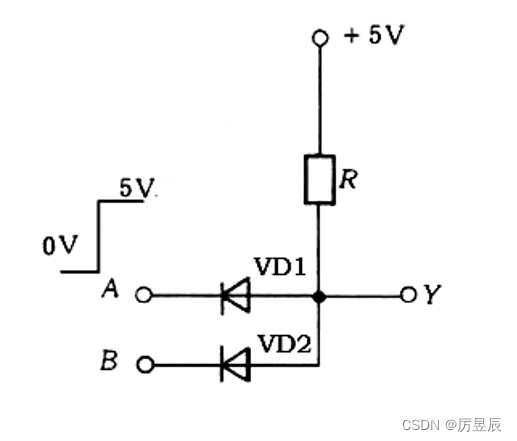
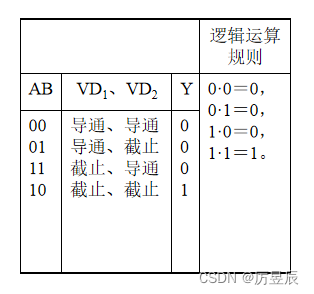
③二极管及电阻组成的与门电路及分析

 

 （2）或门电路

①图形符号

②表达式

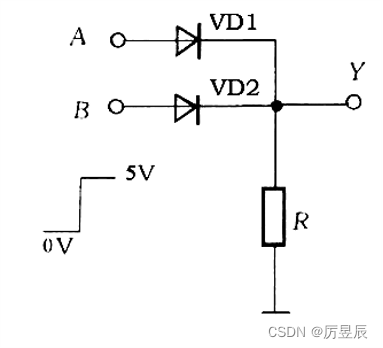
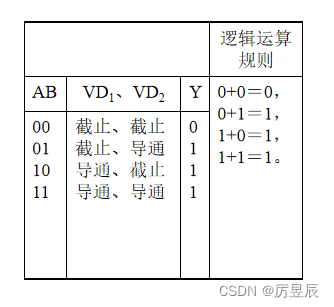
③二极管及电阻组成的或门电路及分析

（3）非门电路

①图形符号

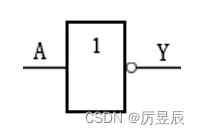
②表达式 

 

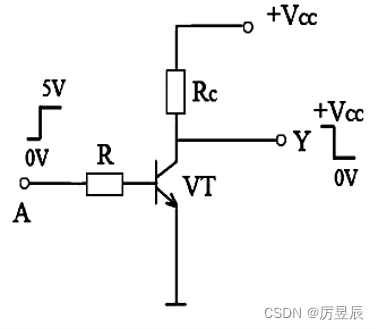
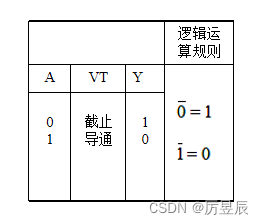
③三极管及电阻组成的非门电路及分析

与门的逻辑功能：有0出0，全1出1

或门的逻辑功能：有1出1，全0出0

非门的逻辑功能：入0出1，入1出0 

三、复合逻辑门电路

定义：与、或、非三种基本逻辑门电路可以组成较复杂的逻辑门电路。

（1）与非电路【有0出1，全1出0】

①图形符号

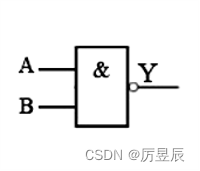
②表达式

③真值表

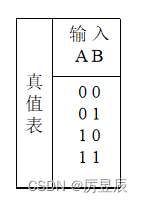
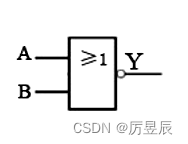
 （2）或非电路【有1出0，全0出1】

①图形符号

②表达式

③真值表

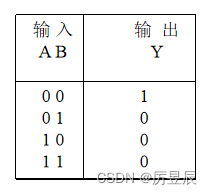
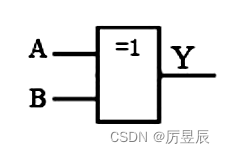
 （3）异或电路【相异出1】

①图形符号

②表达式

③真值表

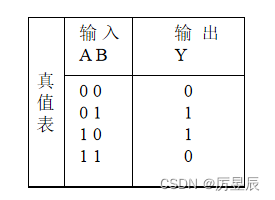
 （4）同或电路【相同出1】

①图形符号

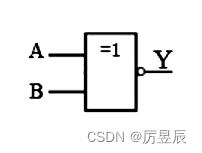
②表达式

③真值表

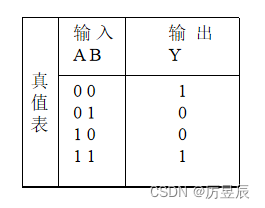
 （5）与或非电路

①图形符号

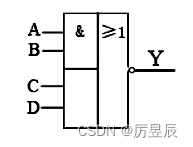
②表达式

---

四、集成逻辑门电路

 定义：采用集成化工艺把分立器件电路制作在一块面积很小的半导体基片上。

按器件的种类可分为：普通三极管型（TTL电路）、场效应管型（MOS电路）。

（1）TTL集成逻辑门电路

①型号及意义

 

②引脚的识读

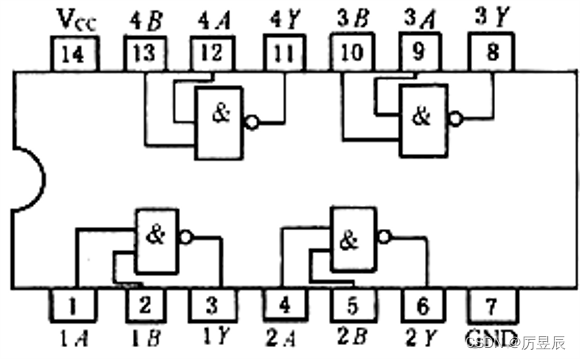
 将集成块正面朝上，引脚朝下，半圆形凹口标置于左端，由左下角起按逆时针方向由下而上依次为1，2，3......14。

：左上角最后边的一个引脚上。

：右下角最后边的一个引脚上。

集成块74LS00内含有4个2输入端与非门。

TTL集成电路的特点

①功耗较大，电源电压必须保证在4.75~5.25V内，建议使用+5V稳压电源供电。

②电源的正负极性不允许接错；

③不使用的多余输入端一般不能悬空；

与门、与非门：通过大电阻接地/接固定的高电平。

或门、或非门：接地。

④输出端不能直接并接，也不能直接与地或电源连接。

（2）CMOS集成逻辑门电路

①型号及意义

 ②种类

特点：功耗很小，价格低，工作速度较低。

CMOS集成电路的特点

①功耗低，电源电压允许波动范围较宽（4.75~18V）；

②电源正负极性不允许接错；

③不使用的多余输入端不能悬空；

与门、与非门：接固定的高电平。

或门、或非门：接地。

④频率较低：CMOS；频率较高：TTL

---