1、二叉树

树是n个节点的有限集
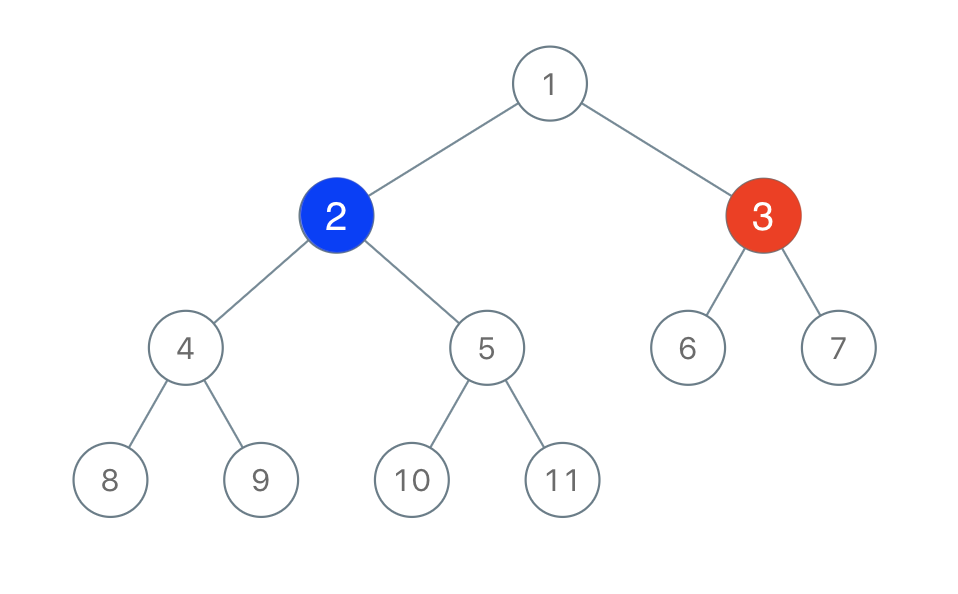
每个节点事多有两颗子树的树称为 二叉树

该实验目标实现以下二叉树：

 

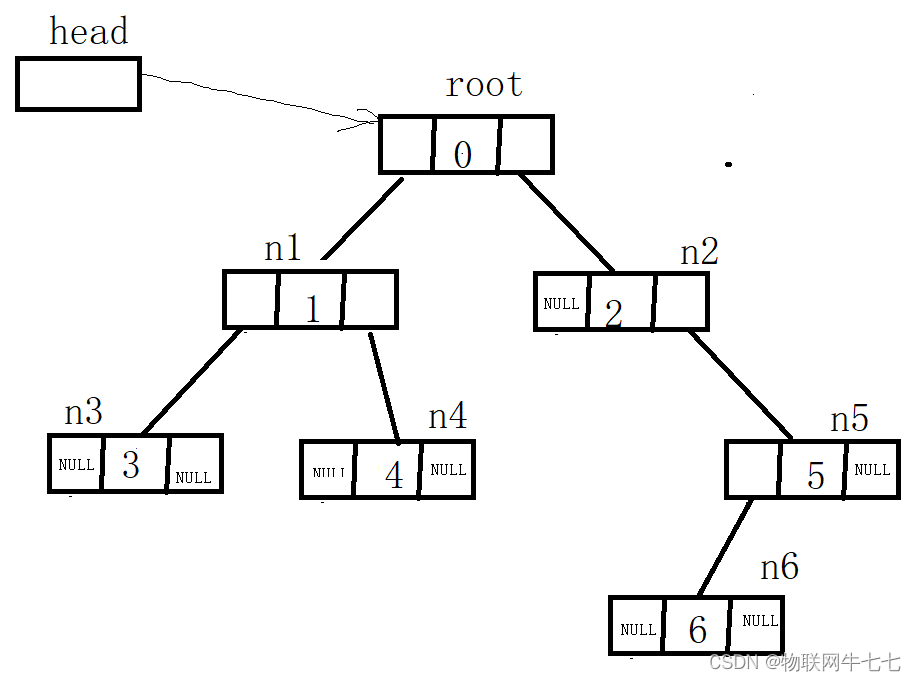
2、二叉树的遍历方案

设：
    D -- 访问根节点，输出根节点;
    L -- 递归遍历左二叉树;
    R -- 递归遍历右二叉树;
    
二叉树遍历方案：
    DLR：先序遍历(先遍历根节点,在遍历左二叉树，再遍历右二叉树)
    LDR：中序遍历(先遍历左节点,在遍历根二叉树，再遍历右二叉树)
    LRD：后序遍历(先遍历左节点,在遍历右二叉树，再遍历根二叉树)
    

3、构造二叉树的节点

    一个成员用来保存左侧子节点的地址
    一个成员用来保存右侧子节点的地址
    一个成员用来保存数据值。
    
   （注意： 如果没有左节点或者右节点赋值为NULL）

typedef struct node
{
	struct node *lchild;
	int data;
	struct node *rchild;
}NODE;

    

4、二叉树遍历的C语言实现

#include<stdio.h>

typedef struct node
{
	struct node *lchild;
	int data;
	struct node *rchild;
}NODE;

// 先序遍历   DLR 
void preOrder(NODE *h)
{
	if(h)
	{
		printf("%d ",h->data);
		preOrder(h->lchild);
		preOrder(h->rchild);
	}
}

// 中序遍历  LDR
void middleOrder(NODE *h)
{
	if(h)
	{		
		middleOrder(h->lchild);
		printf("%d ",h->data);
		middleOrder(h->rchild);		
	}
}

// 后序遍历   LRD 
void postOrder(NODE *h)
{
	if(h)
	{		
		postOrder(h->lchild);
		postOrder(h->rchild);
		printf("%d ",h->data);
	}
}

int main()
{
	// 指向根节点的指针 
	NODE *head;
	
	// 根节点
	NODE root;
	
	// 定义6个节点 
	NODE n1;
	NODE n2;
	NODE n3;
	NODE n4;
	NODE n5;
	NODE n6;
	
	head = &root;
	
	// 构造二叉树 
	root.lchild = &n1;
	root.data = 0;
	root.rchild = &n2;
	
	n1.lchild = &n3;
	n1.data = 1;
	n1.rchild = &n4;
	
	n2.lchild = NULL;
	n2.data = 2;
	n2.rchild = &n5;
	
	n3.lchild = NULL;
	n3.data = 3;
	n3.rchild = NULL;
	
	n4.lchild = NULL;
	n4.data = 4;
	n4.rchild = NULL;
	
	n5.lchild = &n6;
	n5.data = 5;
	n5.rchild = NULL;
	
	n6.lchild = NULL;
	n6.data = 6;
	n6.rchild = NULL;
	
	printf("先序遍历DLR："); 
	preOrder(head);
	printf("\n");
	
	printf("中序遍历LDR："); 
	middleOrder(head);
	printf("\n");
	
	printf("后序遍历LRD："); 
	postOrder(head);
	printf("\n");	
	
	return 0;
}

演示效果：