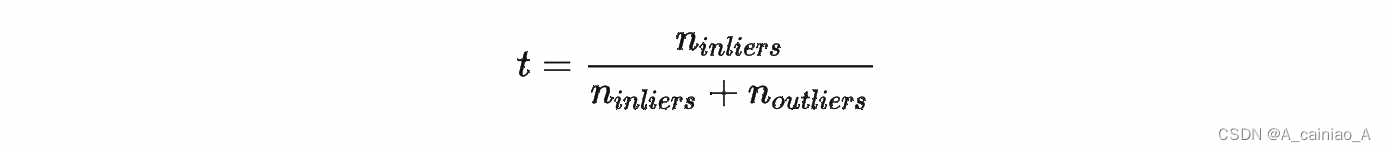机器学习：线性回归分析女性身高与体重之间的关系

创作不易，觉得文章不错或能帮到你学习，记得点赞 + 收藏哦

文章目录

机器学习：线性回归分析女性身高与体重之间的关系
一、实验目的
二、实验原理
三、实验内容
四、实验环境
五、实验步骤
- 业务理解
- 读取数据
- 数据理解
- 数据准备
- 模型类型的选择与超级参数的设置
- 训练具体模型及查看其统计量
- 模型预测
- 模型评价
- 模型优化与重新选择
总结

一、实验目的

1.理解一元线性回归原理

2.掌握Statsmodels 分析模块相应的方法

二、实验原理

线性回归也被称为最小二乘法回归（Linear Regression, also called Ordinary Least-Squares (OLS) Regression）。它的数学模型是这样的：

y = a+ b* x＋e其中，a被称为常数项或截距、b被称为模型的回归系数或斜率、e为误差项。

a和b是模型的参数，当然，模型的参数只能从样本数据中估计出来：y’= a’ + b’* x，我们的目标是选择合适的参数，让这一线性模型最好地拟合观测值，拟合程度越高，模型越好，我们如何判断拟合的质量呢？这一线性模型可以用二维平面上的一条直线来表示，被称为回归线，模型的拟合程度越高，也即意味着样本点围绕回归线越紧密

在这里插入图片描述

如何计算样本点与回归线之间的紧密程度呢？

高斯和勒让德找到的方法是：被选择的参数，应该使算出来的回归线与观测值之差的平方和最小。用函数表示为：
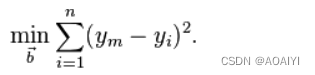
在这里插入图片描述

这被称为最小二乘法，其原理为：当预测值和实际值距离的平方和最小时，就选定模型中的两个参数（a和b）这一模型并不一定反映解释变量和反应变量真实的关系。但它的计算成本低，相比复杂模型更容易解释

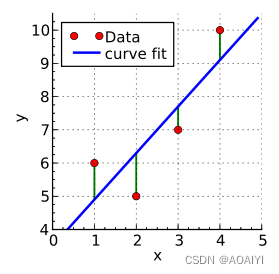
在这里插入图片描述
模型估计出来后，我们要回答的问题是：

我们的模型拟合程度如何？或者说，这个模型对因变量的解释力如何？（R2）
整个模型是否能显著预测因变量的变化？（F检验）
每个自变量是否能显著预测因变量的变化？（t检验）

Statsmodels 是 Python 中一个强大的统计分析包，包含了回归分析、时间序列分析、假设检验等等的功能。可以与 Python 的其他的任务（如 NumPy、Pandas）有效结合，提高工作效率。在本文中，我们重点介绍回归分析中最常用的 OLS（ordinary least square）功能。当你需要在 Python 中进行回归分析时，import statsmodels.api as sm 后，就可以使用其中的方法了。

三、实验内容

利用statsmodels进行最小二乘回归，分析女性身高与体重之间的关系并作出线性回归预测，评估模型。

在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。

本次“线性回归分析女性身高和体重之间关系”，我们将通过以下9个步骤开始进行：

1.业务理解

2.读取数据

3.数据理解

4.数据准备

5.模型类型的选择与超级参数的设置

6.训练具体模型及查看其统计量

7.模型预测

8.模型评价

9.模型优化与重新选择

四、实验环境

Python 3.6.1以上

Jupyter

五、实验步骤

业务理解

分析女性身高与体重之间的关系：分析数据women
在这里插入图片描述

读取数据

#导入pandas库和numpy库
import pandas as pd
import numpy as np
#读取women.csv
df_women = pd.read_csv('women.csv',index_col=0)
#读取前五行数据，如果是最后五行，用df_women.tail()
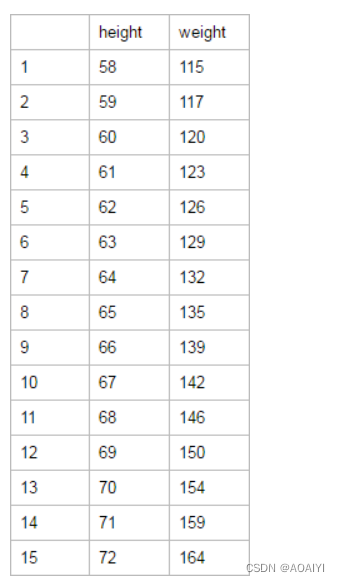
print(df_women.head())

在这里插入图片描述

数据理解

1.查看数据结构

#查看数据的二维结构，即：几行几列
df_women.shape

在这里插入图片描述

说明：women.csv表中共有15行，两列数据

2.查看列名称

#查看数据列名称
df_women.columns

在这里插入图片描述

说明：women.csv中总共两列数据，名称为height和weight

3.查看关于women数据的描述统计

#describe()函数对数据进行描述统计
#describe()对每一列数据进行统计，包括计数，均值，std，最小值，最大值，各个分位数等
df_women.describe()

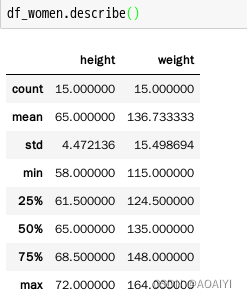
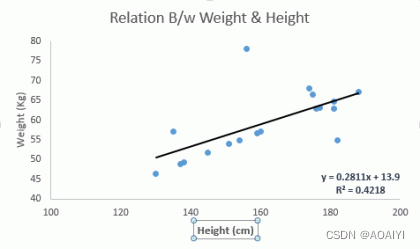
在这里插入图片描述

4.将women.csv中的数据绘制成图表

#数据可视化，将数据以散点图的形式展现出来
#导入可视化库matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
#绘制散点图，横轴为体重，纵轴为身高
plt.scatter(df_women['height'],df_women['weight'])
plt.show()

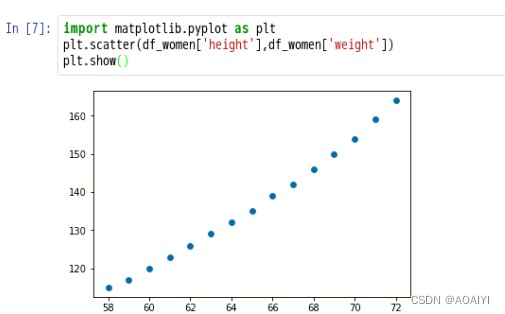
在这里插入图片描述

数据准备

分别获得height和weight这两列数据，做模型预测使用

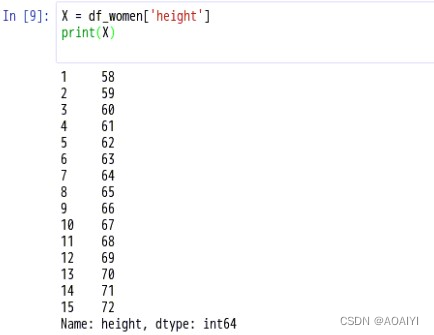
#获得“身高”这一列数据赋给X
X = df_women['height']
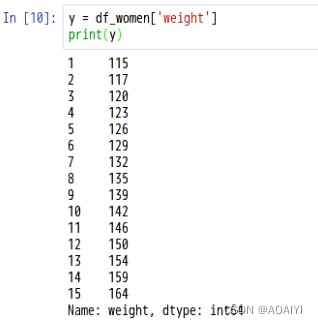
#获得“体重”这一列数据赋给y
y = df_women['weight']
print(X)
print(y)

在这里插入图片描述

模型类型的选择与超级参数的设置

1.导入构建模型需要的库，为模型增加常数项，即回归线在y轴上的截距

Statsmodels 是 Python 中一个强大的统计分析包，包含了回归分析、时间序列分析、假设检验等功能。

Statsmodels 在计量的简便性上是远远不及 Stata 等软件的，但它的优点在于可以与 Python 的其他的任务（如 NumPy、Pandas）有效结合，提高工作效率

#导入构建模型需要的库
import statsmodels.api as sm
from pandas.core import datetools
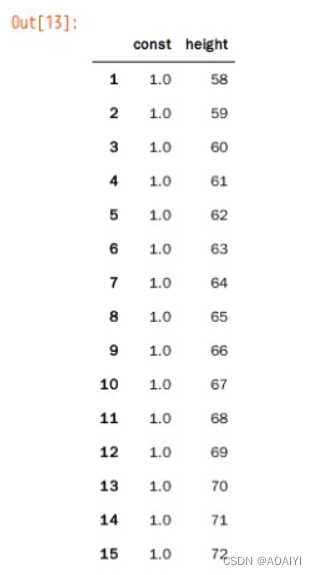
#为模型增加常数项，即回归线在y轴上的截距
X = sm.add_constant(X)
X

在这里插入图片描述
2.执行最小二乘回归

执行最小二乘回归，X可以是numpy array或pandas dataframe（行数为数据点个数，列数为预测变量个数），y可以是一维数组（numpy array）或pandas series

myModel = sm.OLS(y,X)

在这里插入图片描述

训练具体模型及查看其统计量

1.使用OLS对象的fit()方法来进行模型拟合

result = myModel.fit()

.2.查看模型拟合的结果

result.summary()

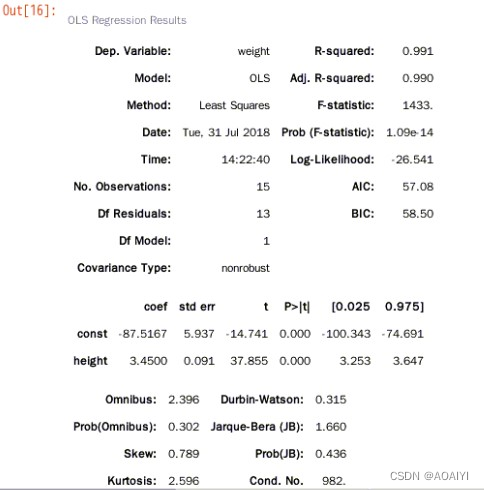
在这里插入图片描述
说明：初学者只关注 summary 结果中的判定系数，各自变量对应的系数值及 P 值即可。

R-squared 在统计学里叫判定系数，或决定系数，也称拟合优度，值在 0 到 1 之间，值越大，表示这个模型拟合的越好，这里 0.991 就拟合的很好

coef：截距

std err ：是标准误差

t 和 P：这是对每个系数做了个统计推断，统计推断的原假设是系数为 0，表示该系数在模型里不用存在，不用理解原理和具体过程，可以直接看 P 值，P 值如果很小，就推断原假设，即其实系数不为 0，该变量在模型中应该是存在的，如上面的 summary 结果，height的 P 值很小，说明这个自变量在模型里都是有意义的，都应该存在模型里。有些回归问题中，P 值比较大，那么对应的变量就可以扔掉

3.查看最终模型的参数coef

result.params

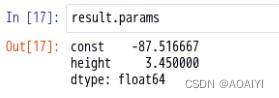
在这里插入图片描述

4.查看判定系数

result.rsquared

在这里插入图片描述

5.看对应的残差

残差表示真实值和模型拟合值的距离。

result.resid

在这里插入图片描述

这里有 15个数据，也就有 15 个残差。

模型预测

计算预测值

#模型预测
y_predict = result.predict()
y_predict

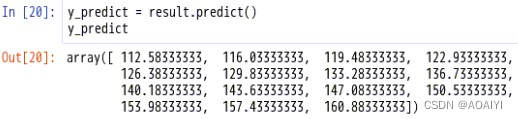
在这里插入图片描述

模型评价

画出预测模型图

#模型评价
#原来数据散点图
plt.plot(df_women['height'],df_women['weight'],'o')
#根据已有身高，按照预测模型作图
plt.plot(df_women['height'],y_predict)
plt.title("Linear regression analysis of female weight and height")
#分别给x轴和y轴命名
plt.xlabel('height')
plt.ylabel('weight ')
plt.show()

在这里插入图片描述

模型优化与重新选择

numpy.column_stack(tup)[source]：Stack 1-D arrays as columns into a 2-D array.

numpy.power(x1, n)：对数组x1的元素分别求n次方

1.模型优化与重新选择

#模型优化与重新选择----------------------------
import  numpy as np
X = np.column_stack((X,np.power(X,2),np.power(X,3)))
X = sm.add_constant(X)
myModel_updated = sm.OLS(y,X)
result_updated = myModel_updated.fit()
print(result_updated.summary())

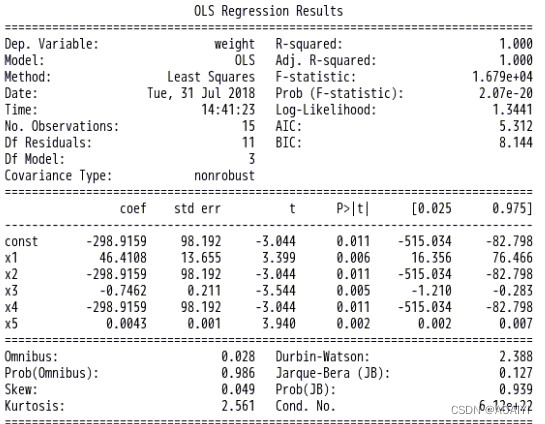
在这里插入图片描述

2.对模型进行预测

y_predict_result_updated = result_updated.predict()
y_predict_result_updated

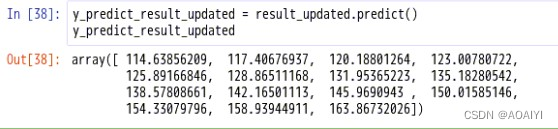
在这里插入图片描述

3.查看参数

result_updated.params

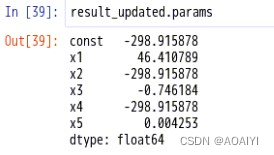
在这里插入图片描述

4.查看残差

result_updated.resid

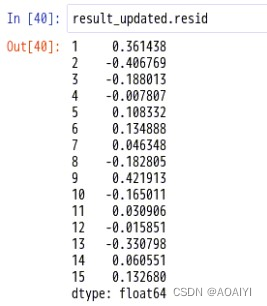
在这里插入图片描述

5.查看残差的std

result_updated.resid.std()

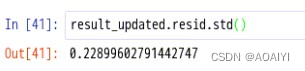
在这里插入图片描述

6.对优化后的模型作图

plt.rcParams['font.family']='simHei'
plt.scatter(df_women['height'],df_women['weight'])
plt.plot(df_women['height'],y_predict_result_updated)
plt.title("Linear regression analysis of male weight and height")
plt.xlabel('height')
plt.ylabel('weight')
plt.show()

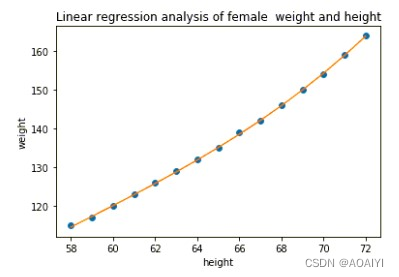
在这里插入图片描述
由此图得知，预测值和实际值更加接近。

总结

为什么纸上谈兵不行？纸上谈兵太理想化了，把自己没有发现的问题隐藏了，当成了不存在的问题。只有实际多多亲自动手，才会发现有太多的问题是书上没提到的，也是自己没想到的。才会发现，一个小小的问题也要搞上半天。当然，如果你基础巩固的话，那这些问题应该都是可以被你解决的。熟练后，就不认为这些问题了。
不要看代码不难就感觉会了，只有自己的手打一遍，没有错误，编程的严谨些决定了，你错一个字母都不行。所以大家一定要注意，编程是自己打出来的，不是复制，粘贴你就会了，以后碰到了，还是不会。