目录
- RANSAC
- 算法基本思想和流程
- 迭代次数推导
- 参考
RANSAC
RANSAC(RAndom SAmple Consensus,随机采样一致)算法是从一组含有外点(outliers)的数据中正确估计数学模型参数的迭代算法。“外点”一般指的的数据中的噪声,比如说匹配中的误匹配和估计曲线中的离群点。所以,RANSAC也是一种“外点”检测算法。RANSAC算法是一种不确定算法,它只能在一种概率下产生结果,并且这个概率会随着迭代次数的增加而加大。
- 内点:符合模型的数据,或者说带入模型后误差小于阈值
- 外点:不符合模型的数据,或者说带入模型后误差大于阈值
算法基本思想和流程
RANSAC是通过反复选择数据集去估计出模型,一直迭代到估计出认为比较好的模型。
具体的实现步骤可以分为以下几步:
- 选择出可以估计出模型的最小数据集
- 使用这个数据集来计算出数据模型
- 将所有数据带入这个模型,计算出“内点”的数目
- 比较当前模型和之前推出的最好的模型的“内点“的数量,记录最大“内点”数的模型参数和“内点”数
- 重复1-4步,直到迭代结束或者当前模型已经足够好了(“内点数目大于一定数量”)
迭代次数推导
假设“内点”在数据中的占比为
t
t
t
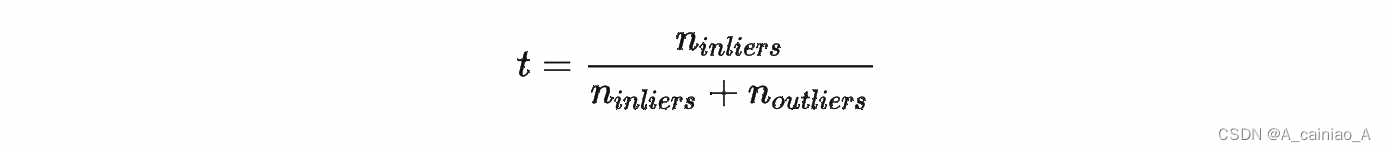
那么每次计算模型使用
N
N
N 个点的情况下,选取的点至少有一个外点的概率:
1
−
t
N
1 - t^N
1−tN
在迭代
k
k
k 次的情况下,
k
k
k 次计算模式都至少采样到一个外点的概率:
(
1
−
t
N
)
k
(1-t^N)^k
(1−tN)k
则采样到正确的
N
N
N 个点去计算出正确模型的概率:
P
=
1
−
(
1
−
t
N
)
k
P = 1 - (1-t^N)^k
P=1−(1−tN)k
可以求得:
k
=
l
o
g
(
1
−
P
)
/
l
o
g
(
1
−
t
N
)
k = log(1-P) / log(1-t^N)
k=log(1−P)/log(1−tN)
“内点”的概率 t t t 通常是一个先验值。 P P P 是我们希望RANSAC得到正确模型的概率。如果事先不知道 t t t 的值,可以使用自适应迭代次数的方法。也就是一开始设定一个无穷大的迭代次数,然后每次更新模型参数估计的时候,用当前的“内点”比值当成 t t t 来估算出迭代次数。
参考
RANSAC算法详解(附Python拟合直线模型代码)