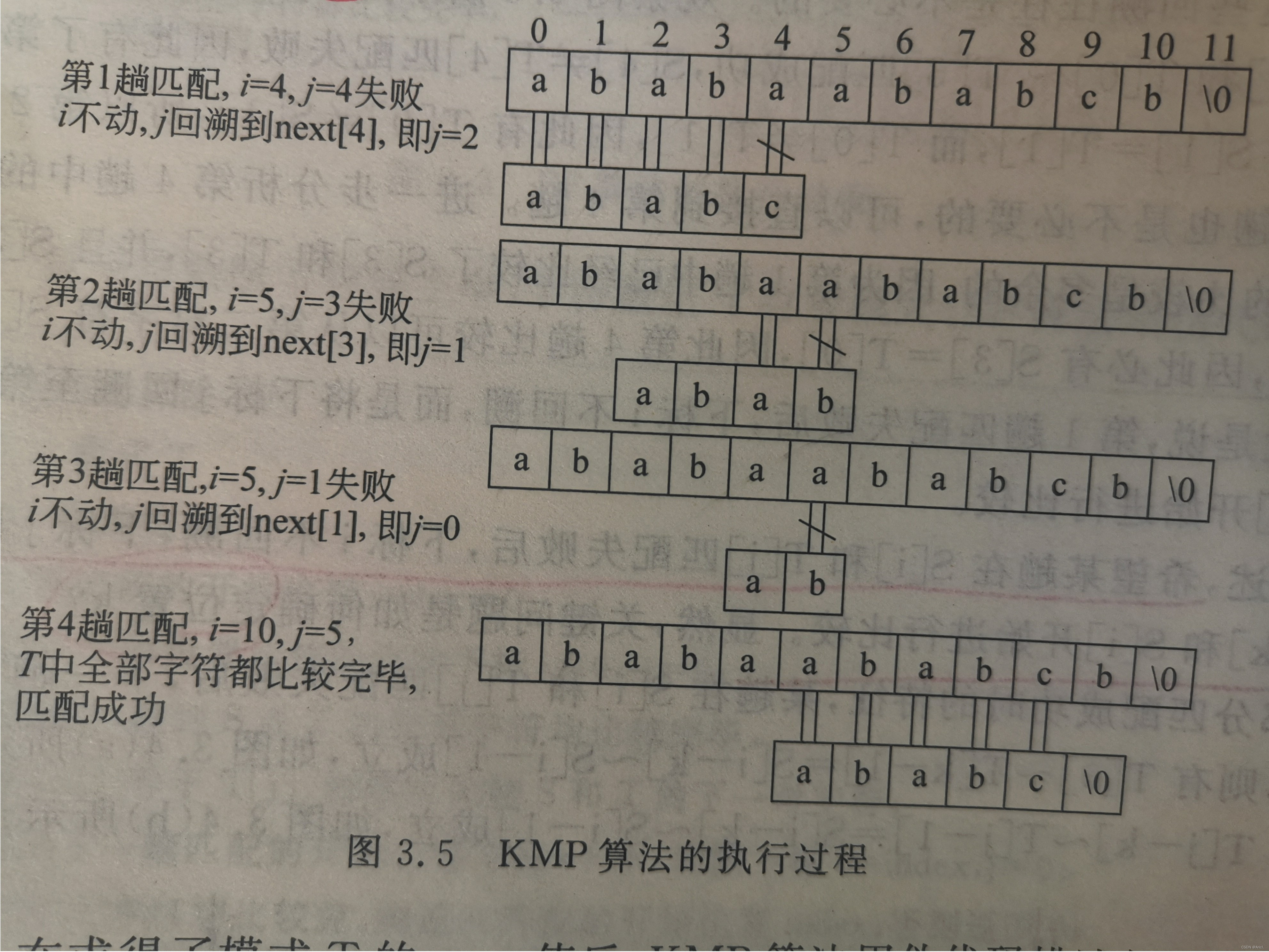
算法核心思想

        在BF算法的基础上加以改进，BF算法中每次当前字符不相等时，主串S要回溯到其下一个字符处，模式串T要回溯到 j=0 位置进行下一趟的匹配。然而，大多数情况下，这种回溯是没有必要的，非常耗时且效率低，是一种蛮力的思想。

        KMP算法在此基础上对其做了改进，就是增加了next数组，里面存放的值就是每次匹配失败后模式串T要回溯的下标位置，所以KMP算法的核心就在于如何求模式串T的next数组，至于后面的串匹配过程和BF算法原理一致。

 

 

 代码

#include<iostream>
#include<cstring>
using namespace std;
int next[]={0};
//求next值
void getNext(char T[],int next[]){
	int j=0,k=-1;
	next[0]=-1;
	while(T[j]!='\0'){
		if(k==-1){
			next[++j]=0;
			k=0;
		}
		else if(T[j]==T[k]){
			k++;
			next[++j]=k;
		}else {
			k=next[k];
		}
	} 
} 

//串匹配
int KMP(char S[],char T[]){
	int i=0,j=0;
	while(S[i]!='\0'&&T[j]!='\0'){
		if(S[i]==T[j]){
			i++;
			j++;
		}else{
			j=next[j];//不相等时，模式串回溯到对应的next值下标位置
			if(j==-1){
				i++;
				j++;
			} 
		}
	} 
	//当模式串全部被遍历完后，说明匹配成功，返回匹配成功时的开始位置 
	if(T[j]=='\0'){
		return (i-strlen(T))+1;
	}else{
	    return 0;	
	}	
} 
 
int main(){
	char S[]="abcabcacb";
	char T[]="abcac";
	cout<<"S="<<S<<endl;
	cout<<"T="<<T<<endl;
	getNext(T,next);//获取模式串T的next数组值
	int n=KMP(S,T);
	cout<<"模式串T的next数组值为："<<endl;
	for(int i=0;i<5;i++){
		cout<<next[i]<<"  ";
	}
	cout<<endl;
	if(n!=0){
		cout<<"串匹配成功，起始位置为"<<n<<endl; 
	}else{
		cout<<"串匹配失败！"<<endl;
	}
	return 0;
} 

运行

 这里推荐一篇深入分析KMP算法的优质文章，三金大佬写的！

KMP算法真的有这么难吗？（清晰详细版）https://blog.csdn.net/QAZJOU/article/details/126765353?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167538890716800215074340%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=167538890716800215074340&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-1-126765353-null-null.142^v72^insert_down4,201^v4^add_ask&utm_term=%E4%B8%89%E9%87%91kmp%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187END.