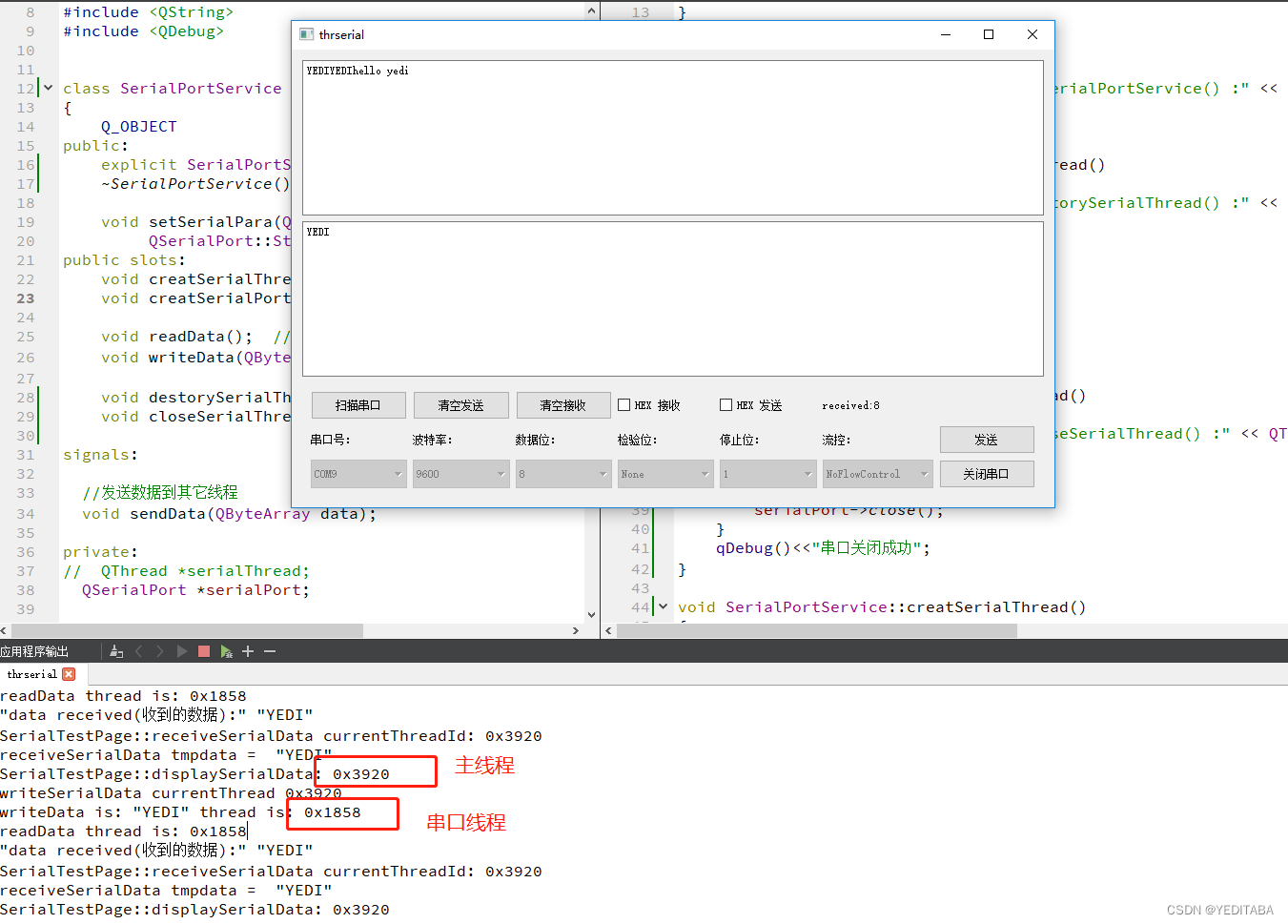
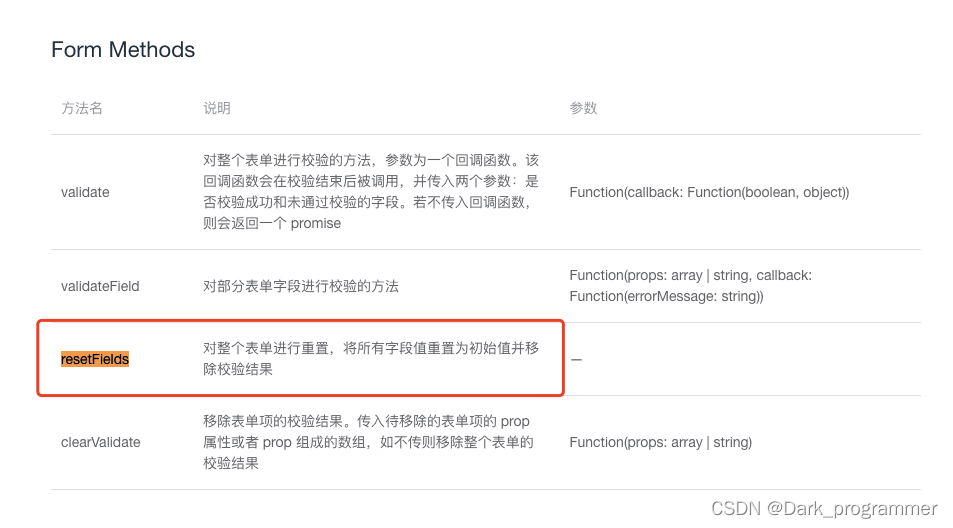
文本分析：非结构化信息分析科学与应用导论（主题建模）

1.介绍

文本聚类可以将数据（这里即指文本）按照一定规则划分为不同的群组，理想情况下可以从聚类结果中发现一些有趣的模式。不同聚类方法的一致性意义和划分方式也不同。尽管它们有各自的用武之地，但它们无法发现这些群组中任何隐藏结构。

例如，考虑以下国际媒体上的新闻标题，且没有其他的知识来源：

1. Amazon’s virtual assistant could witness a homicide in Florida.（亚马逊的虚拟助手可以目睹佛罗里达州的一起凶杀案。）
2. Auto sales in Mexico hit low records due to pandemic.（由于大流行，墨西哥的汽车销量创下新低。）
3. High-speed trains are close to doubling their speed.（高速列车的速度接近翻倍。）
4. Flower market in Mexico closed due to covid-19.（墨西哥花卉市场因 covid-19 而关闭。）
5. Coronavirus could last 3 more years in the United States.（冠状病毒在美国可能还会持续 3 年。）

很容易发现：(1) 和 (3) 是关于技术组成的 Group1，(2)、(4) 和 (5) 是关于 covid-19 的 Group2。当然，任何一种聚类方法应该也会得出同样的结论。现在假设有一个 “隐藏的” 结构，它连接着 Group1 的单词，而另一个结构则连接着 Group2 的单词（即，哪些术语对描述每个组更重要？）。如果能 “发现” 这些结构，不仅可以将新文档合并到一个组中（因为知道管理该组的模型），而且还知道这些结构将提供有关每个小组 “谈论” 的主题信息。随着要分析的新闻数量开始增加，决定结构将变得越来越复杂。另一方面，你肯定会注意到，Group1 谈论的是技术相关的问题，而 Group2 谈论的是冠状病毒相关的问题。然而，要做出这样的推断，必须使用在过去看到的类似情况的经验。但不幸的是，传统的聚类方法无法确定这样的结构，也无法知道它指的是什么，除非为它提供额外的知识来源。

为了发现这样的隐藏结构，我们定义一个生成过程，该过程描述了 文档是如何通过出现在类似上下文中的单词生成的。基于这个假设，我们可以推断出模型的隐藏结构，即 与文档相关的主题的形式。执行这项任务的最常见的生成模型类型之一被称为 主题模型。主题模型 可以帮助我们组织和提供想法，使我们能够理解文档语料库中的关系。

主题建模是一种无监督机器学习方法，它可以从文档体中发现隐藏的语义结构。这些结构通常在文档中以相似单词或短语的形式出现，它们会自动分组以表征主题。

由于文档处理特定的主题，人们会期望特定的单词更频繁地出现在某个文档中。例如，“比赛” 和 “球场” 一词在谈论足球的文本中出现更频繁，“桌子和球” 一词出现在有关乒乓球的文本中，“球员” 在两者中出现相同。通常，一个文档以不同的比例包含多个主题；因此，在一份 $10\%$ 关于乒乓球和 $90\%$ 关于足球的文本中，足球单词的数量可能是乒乓球单词的 $9$ 倍。

因此，主题模型以一种直觉的方式检查文本语料库，基于单词的统计分布发现主题，以及每个文本的主题分布。

2.主题建模

主题建模作为一种文本分析技术，允许在文档集合中发现主题。主题包含经常同时出现的单词组。主题模型可以连接具有相似含义的单词，并且可以区分多种含义的不同用法。由于文档是由单词组成的，一个主题可以包含在多个文档中，那么一个主题就可以被表示为强关联词的组合。此外，任何文档都可能与多个主题相关联（Atkinson et al.，2016；Aggarwal，2018）。因此，主题建模是指基于两个假设对文档集合（即语料库）进行划分的过程。

1. 每个文档都被视为主题的混合物。主题的分布可以通过 “组合” 所覆盖主题的所有分布来获得。假设每个文档可以以不同的比例包含来自多个主题的单词。例如，在两个主题 $A$ 和 $B$ 的模型中，可以说文档 $1$ 是主题 $A$ $90\%$，主题 $B$ 是 $10\%$，而文档 $2$ 是主题 $A$ $30\%$，主题 $B$ 是 $70\%$。
2. 每个主题都被看作是单词的混合物。假设从新闻文章中发现两个主题 $A$ 和 $B$ 的模型，但它们的含义是未知的。与主题 $A$ 相关的最常见的词可能是 “总统”、“国会” 和 “政府”，而对于主题 $B$，这些可能是 “电影”、“电视” 和 “演员”。没有人告诉你主题 $A$ 或主题 $B$ 指的是什么，也没有任何历史信息用来推断；但你可能已经看出来，主题 $A$ 可能指的是政策问题，而主题 $B$ 指的是娱乐主题。另外要注意，在主题之间可以共享一些单词。例如，“预算” 这个词可以出现在这两个主题中。

简单地说，混合或混合分布是指两个或多个概率分布的组合。随机变量从多个原始总体中抽样，以创建一个新的分布。分布可以由不同类型的分布（如正态分布、多项式分布等）构成，或者是具有不同参数的相同类型的分布。例如，下图显示了三种正态分布的混合（高斯混合模型)，每个模型都有不同的平均值。

主题建模技术需要判断文档中存在哪些主题，以及基于混合分布的这种主题存在概率大小为多少。建模主题有多种方法，最流行的是潜在语义分析（Latent Semantic Analysis，LSA）的一种变体，称为概率潜在语义分析（probabilistic Latent Semantic Analysis，pLSA）和潜在狄利克雷分配（Latent Dirichlet Allocation，LDA）（Aggarwal, 2013; Atkinson et al., 2016; Beaujean, 2014; Aggarwal, 2018）。

LSA 是一种无监督算法，它从一个低维的语料库中生成单词或文档的语义空间。基于生成的向量表示，我们可以认为单词的向量可以用主题来表示，这对应于原始数据的简化维数。一般来说，LSA 快速高效，但作为主题模型它有三个弱点：

1. 向量是不可解释的，所以不能确定这些主题是关于什么的。
2. 要获得准确的结果，需要大量的语料库和词汇量，这影响了计算效率和词汇量管理。
3. 生成的表示效率没有那么高，所以当维数增加时，在表示单词的意义时会产生很多噪声。

为了解决这些问题，pLSA 使用了一种概率方法，而不是 SVD（Klein, 2015）。其主要思想是找到一个主题或潜在结构的概率模型，它可以生成从最初的 文档 - 词语 矩阵（$D\times W$） 中观察到的数据。假设 $P(D,W)$ 即是我们正在寻找的模型，那么对于任何文档 $d$ 和单词 $w$，$P(d,w)$ 即是矩阵中对应的值。尽管 pLSA 处理这个问题的方式不同于 LSA（Landauer et al., 2014），但它只是在原始模型上增加了对主题和单词的概率处理；因此，与其他技术相比，它有两个缺点：

• 没有模型 $P(D)$ 的参数，因此为新文档分配概率的方法是未知的。
• 参数的数量随文档的数量呈线性增长，因此概率方法容易发生过拟合。

因此，pLSA 并未被广泛使用，所以在寻找主题模型时，更多地会选择诸如 LDA 之类的方法，因为它以某种方式扩展了 pLSA 来解决上述问题。

3.LDA

LDA（Latent Dirichlet Allocation）是一种用于主题建模的生成模型，它将语料库中的每个文档转换为一组主题，这些主题涵盖了文档单词的重要部分。这是可以实现的，假设文档是用一定的单词分布编写的，并且这种分布决定了主题，忽略了单词的顺序（即不考虑语法）。

LDA是建立在两个基本的假设之上的：

1. 分布假设：构建相似的主题使用相似的词。
2. 混合假设：根据文档对各种主题的讨论，从而可以确定混合主题的统计分布。

一般来说，LDA 分配了一个包含两个输出的主题模型：

1. 一个包含经常同时出现的词组的主题列表。
2. 一个与每个主题密切相关的文档列表。

理想情况下，每个主题都应该与其他主题区分开来。为此，该方法假设文档中的所有单词都可以被分配到属于某一个主题的概率，并且主题或潜在变量是独立的。为此，我们使用狄利克雷分布（Beaujean，2014），它允许我们对 文档 - 主题 分布和 主题 - 单词 分布进行建模。我们可以把狄利克雷看作是分布上的分布，这就回答了一个问题：“鉴于这种类型的单词分布，我看到的当前概率分布将是什么？”从技术上讲，狄利克雷是 Beta 分布的多元推广（Baron，2019）。

为了直观地理解主题分配是如何工作的，假设我们必须在一个语料库上比较主题混合的概率分布，该语料库中的文档包含三个未知的不同的主题（$A$、$B$ 和 $C$）。这个模型的分布将会给特定主题非常高的权重，并且不会给其他主题过多的权重。因此，如果我们有三个主题，我们希望看到的概率分布可以表示为主题的混合：

• 混合 $X$： $90\%$ 主题 $A$，$5\%$ 主题 $B$，$5\%$ 主题 $C$
• 混合 $Y$： $5\%$ 主题 $A$，$90\%$ 主题 $B$，$5\%$ 主题 $C$
• 混合 $Z$： $5\%$ 主题 $A$，$5\%$ 主题 $B$，$90\%$ 主题 $C$

如果我们从这个狄利克雷分布中选择一个随机概率分布，参数化在每个主题的权重，我们可能会得到一个分布，且非常类似于混合 $X$，混合 $Y$ 或混合 $Z$。

因此，从 $33\%$ 主题 $A$，$33\%$ 主题 $B$，$33\%$ 主题 $C$ 的分布中生成样本的概率极小。这就是狄利克雷分布基本提供的：一种对特定类型的概率分布进行抽样的方法。形式上，狄利克雷分布在概率单纯形（probability simplex）上抽样，即在一组加起来为 $1$ 的数字上抽样，例如，$(0.6,0.4)$，$(0.1,0.1,0.8)$，它们代表 $K$ 个不同类别或主题的概率。在示例中，$K=3$ 的情况下，可以生成一个表示 $\alpha$ 值的 $K$ 维向量的模型。

当处理类别分布并且我们不确定分布时，将不确定性表示为概率分布的最简单方法是狄利克雷分布。一个 $K$ 维的狄利克雷有 $K$ 个正数参数（可以归一化来表示概率），这些参数构成狄利克雷的平均值。因此，所有的样本都将以这个单纯形为中心。离单纯形中的某个点越远，它通常代表 $K$ 个维数中的一个角，例如 $(0,0,1,0)$。可以从几何的角度进行简单的理解，如下图所示。这是一个由蓝色数据点表示的 $8$ 个文档组成的语料库，假设词汇表由三个单词组成（即每个文档都是一个三维向量），其轴表示每个单词的多项式概率分布 $(\theta )$。此外，我们还选择了表示 $K=2$ 的主题。

多项式分布是一种概率分布，用于计算涉及两个或多个随机变量（比如文档中单词的出现）的实验结果。$n$ 次实验的多项分布概率如下：

每个文档可以包含一个或多个词汇，但具有不同的出现概率，其中多项分布 $\theta$ 要求值之和为 $1$，即 $P(word1)+P(word2)+P(word3)=1$。此外，每个文档可以涵盖 $K=2$ 个可能的主题，因此生成的模型是两个主题的混合。反过来，与每个主题相关联的每个单词都有一定的概率分布。因此，主题可以看作是语料库词汇表上的概率分布。如果我们观察由三个轴组成的三角形，那么我们想知道其每个点的概率密度。

形式上，狄利克雷分布定义了向量 $\alpha$ 中 $k$ 个分类（局部）值条目的概率密度，该向量 $\alpha$ 与多项式参数 $\theta$ 具有相同数量的特征。对于一定数量的主题 $k$，具有参数 $\alpha$ 或 $Dir(\alpha )$ 的狄利克雷被定义为：

上述公式中 $\Gamma$ 是伽马（Gamma）分布（Baron, 2019）。$p(\theta \mid \alpha )$ 试图回答这个问题：在狄利克雷分布的参数是 $\alpha$ 的情况下，与 $\theta$ 分布相关的概率密度是多少？在形式上，文档与主题之间 以及 单词与主题之间 的这些依赖关系可以用一种简单的贝叶斯方法进行建模，如下图所示：

• 给定一个文档 $d$，主题 $z$ 以 $P(z|d)$ 的概率出现在该文档中。
• 给定一个主题 $z$，由 $z$ 生成一个单词 $w$，其概率为 $P(w|z)$。

文档、主题和单词之间的依赖性建模

形式上，观察文档 $D$ 和单词 $W$ 的联合概率为：$$P(D,W)=P(D)\sum _{Z}P(Z|D)P(W|Z)$$

直观地说，方程的右边告诉我们观察某些文档 $D$ 的可能性有多大，然后，根据该文档中主题 $Z$ 的分布，在该文档中找到某个单词 $W$ 的可能性有多大。

在这种情况下，$P(D)$、$P(Z|D)$ 和 $P(W|Z)$ 是模型参数，其中 $P(D)$ 可以直接从语料库中估计，$P(Z|D)$ 和 $P(W|Z)$ 被建模为多项分布 $(\theta )$，可以使用期望最大化算法（Baron, 2019）。如果把这个公式看作是一个生成过程，$P(D,W)$ 等价于以下使用三个不同参数的表达式：$$P(D,W)=\sum _{Z}P(Z)P(D|Z)P(W|Z)$$

我们从主题 $P(z)$ 开始，然后文档用 $P(d|z)$ 独立生成，单词用 $P(w|z)$ 独立生成，假设这些主题是相互独立的。狄利克雷分布提供了一种方法对这个概率分布进行抽样。

从文档、主题和单词的抽样中，该方法扩展到根据狄利克雷分布对主题进行建模，生成一个表示文档主题（或主题混合）分布的随机样本。从主题的分布 $(\theta )$ 中，根据这个分布选择一个主题 $Z$。然后，从另一个狄利克雷分布 $Dir(\beta )$ 中，选择一个随机样本来表示主题 $Z$ 的单词分布。最后，从单词分布 $(\phi )$ 中，选择一个单词 $w$。

使用 LDA 执行主题分配的方法总结如下：

1. 给定一些文档 $M$，一些主题 $K$，词汇表长度为 $N$。
2. 估计超参数 $\alpha$ 和 $\beta$。
3. 对于每个文档 d ∈ { 1 … M } d∈\{1…M\} d∈{1…M}：
   • 从 $Dir(\alpha )$ 中选择 $\theta$（主题分布）。
     • ${\Theta }_{dk}$ 是一个文档 d ∈ { 1 … M } d∈\{1…M\} d∈{1…M} 有一个主题 k ∈ { 1 … K } k∈\{1…K\} k∈{1…K} 的概率。
   • 从 $Dir(\beta )$ 中选择 $\phi$（单词分布）。
     • ${\phi }_{kv}$ 是一个单词 v ∈ { 1 … N } v∈\{1…N\} v∈{1…N} 在一个主题 k ∈ { 1 … K } k∈\{1…K\} k∈{1…K} 的概率。
   • 对于文档 $d$ 中的每个单词 $W_i$：
     • 从多项式分布 $({\theta }_d)$ 中选择一个主题 $Z_i$。
     • 从多项式分布 $({\phi }_{Z_i})$ 中选择一个单词 $(W_i)$。

如果选择的主题 $K$ 少于文档的数量，那么所产生的效果降低了原始语料库的维数。一旦这些潜在变量或隐藏主题在更小的维度上被获得，则可以应用其他无监督学习技术。

由于必须估计使 $p(w;\alpha ,\beta )$ 最大化的参数 $\phi ,\theta$，因此我们需要得到分别控制文档和主题相似性的超参数 $\alpha$ 和 $\beta$：

• $\alpha$ 参数表示文档和主题之间的密度。
  • 一个较低的 $\alpha$ 值（低于 $1.0$）将为每个文档分配较少的主题。例如，可以看到许多主题分布样本在三维空间的角落里。如果 $\alpha$ 值过低，会显示其中只有一个元素是 $1$，其余所有元素都是 $0$，即 $(1,0,0)$，这表明文档只有一个主题。如果 $\alpha$ 的值为 $1.0$，则表示图中三角形表面上的任何空间都分布均匀。
  • 一个较高的 $\alpha$ 的值（大于 $1.0$）将为每个文档分配许多主题，从而生成关于它们所包含的主题更相似的文档。这意味着样本将开始聚集在图的三角形的中心。也就是说，随着 $\alpha$ 值的增加，样本很可能是均匀的，也就是说，它们代表了所有主题的混合物。
• $\beta$ 参数表示主题和单词之间的密度。
  • 一个较小的 $\beta$ 值将使用很少的单词来建模一个主题。反之，较大的 $\beta$ 值将使用更多的单词，从而产生与它们所包含的单词更相似的主题。

有了这些参数，LDA 试图为每个主题找到最佳模型；也就是说，在分布中浓度最高的模型。

例如，下图显示了三维参数 $\alpha$ 如何控制分布的形状。特别要注意的是，$\alpha$ 的值的总和控制着该分布的强度（例如，它的峰值有多大）。随着 $\alpha$ 值的增加，分布更加集中在单纯形的中心，如图所示，数据点为红色（单词）。另一方面，如果这个和接近 $0$，分布将倾向于集中在比例较小的点上。

为了估计产生最佳浓度的超参数，我们通常需要使用参数估计和推理方法。尽管这个问题通常很难解答，但有一些近似方法，如吉布斯采样（Gibbs sampling）、期望最大化（EM）和变分推理（Baron, 2019; Bishop, 2006）。

作为 $K=3$ 时的主题模型的一个例子，下图显示了具有 LDA 调整参数的特定文档。该结果使用主题之间的多维尺度距离（Baron, 2019）进行可视化。

对于所选的主题，如主题 $3$（红色），右图显示了与该主题相关联的单词的分布结果。单词可以在主题之间共享，但强度不同；因此，对于每个单词的总频率，其中一部分对应于当前主题的频率（红色），而其余部分对应于其他两个主题（浅蓝色）。

4.评估

有一种假设认为，LDA 发现的潜在结构通常是重要的和有用的。然而，在无监督学习中，评估这一点是非常具有挑战性的。理想情况下，我们希望捕获信息，以确定是否已经学习了正确的东西，在一个简单的指标中，可以最大化和比较。

为了解决上述问题，有两种评估方法（Beaujean，2014）：

• 内在评估指标：它们衡量该方法捕获模型语义或连贯性以及解释主题的能力，从而减少决策中的不确定性。
• 外在评估指标：衡量该模型在执行特定的预定义任务方面的能力，如评分或监督学习。

最流行的方法包括困惑度（perplexity）和主题连贯性（topic coherence）。困惑度是一种对不确定性的统计度量，所以一个好的模型是一个具有低困惑度的模型。在一个变量 $x$ 上的概率分布 $p$ 的困惑度可以计算为：$2^{-{\sum }_{x}p(x)lo{g}_{2}p(x)}$。理解这个度量的一个直观方法是概率模型对未知样本的预测程度。在 LDA 的情况下，可以估计给定值 $K$ 的主题模型。然后，给定主题所代表的单词分布，我们可以将它们与当前的主题混合或语料库文档中的单词分布进行比较。

下图显示了不同数量的主题 $K$ 的困惑度值，在 $K=6$ 时达到最小值。然而，基于此度量优化模型不会产生可解释的结果；因此，我们需要其他指标。

由 LDA 产生的潜在结构的质量也可以评估主题的连贯性（topic coherence）。一般来说，如果一组表达或事实相互支持，就说它们是连贯的。这种方式下，主题连贯性通过计算 主题上高权重词之间的语义相似度 来衡量单个主题。这有助于区分语义可解释的主题和作为统计推断对象的主题。主题连贯性被应用于每个主题中的最佳单词，并被定义为每个主题中的单词之间的相似性得分的平均值。这种相似性可以用各种方法来衡量，包括：

• C_v：测量主题中移动窗口中单词的共现性，并使用这些值来计算 $N$ 个最佳单词和其他最佳单词的 归一化成对互信息（Normalized Pairwise Mutual Information，NPMI）。
• U_mass：这将分别通过比较一个单词与前一个单词以及后面的单词来衡量共现性。这使用了一个对应于对数条件概率的成对计算函数。

一个好的模型将产生连贯的主题，即具有高连贯分数的主题。下图显示了连贯性（以 u_mass 计算）与不同主题数量之间的关系。由于分数似乎随着主题数量的增加而增加，因此在减少之前选择给出最高分数值的模型是有意义的，所以在这种情况下，我们选择 $K=6$。

一般来说，LDA 通常比 pLSA 工作得更好，因为它可以很容易地推广到新的文档中。如果我们以前没有见过文本在语料库中，则没有那个数据点。为了解决这个问题，LDA 使用语料库作为训练数据来估计 文档 - 主题 分布的狄利克雷分布，然后从那里开始。

5.总结

有几种方法来聚类单词或文档。然而，其中一些没有考虑与这些聚类相关的数据分布。解决这个问题的一种方法是创建主题模型，这些模型比传统方法更容易解释。有几种建模主题的技术，包括 LSA、pLSA 和 LDA。其中最流行的一个是 LDA，因为它有一个健壮的模型，可以说明如何采样文本数据，以便有效地生成与文档相关的主题的分布和与主题相关的单词的分布。

6.实战

本节展示了一个将 LDA 方法应用于主题建模的示例。

对于本示例，您必须从图书网站下载 “lda.py” 程序。我们需要导入一些已经在 “utils.py” 程序中定义的函数，并安装 pramiko 包，它允许连接到显示服务器，以及 pyLDAvis 包，它允许您查看主题模板结果：

pip install paramiko
pip install pyLDAvis

然后，导入了先前定义的 Gensim 包，用于语料库的管理和模型的一致性的评估，以及用于主题可视化的 pyLDAvis 包：

import gensim
from gensim import corpora
from gensim.models.coherencemodel import CoherenceModel 
import pyLDAvis
import pyLDAvis.gensim as gensimvis

因为我们需要重用在 “utils.py” 中定义的函数，所以将它们也加载到程序中：

from past.builtins import execfile 
execfile('utils.py')

我们需要定义一个函数来预处理语料库的内容。

def PreProcessingwithNouns(texts):
	cleanText = []
	pattern = r'(\w+)/(PROPN/NOUN)'
	for text in texts:
		text = List_to_Sentence(ExtractNounsFromLine(pattern,text))
		text = RemoveStopwords(text)
		text = Lematize(text)
		text = RemoveNumbers_Puntuactions(text)
		if len(text)!=0:
			text = regex.sub('+', ' ', text)
			tokens = Tokenize(text)
			cleanText.append(tokens)
	return(cleanText)

此外，在这个函数中，也重用了相同的函数 ExtractNounsFromLine(…)，该函数在第 $5$ 章的练习中定义，从 POS 标记的行中提取名词。

现在，我们需要一个函数，它允许我们以一种可访问的方式查看为语料库及其字典生成的主题模型。这个函数（gensimvis.prepare(…)）为可视化准备数据，生成 vis_data 结构，然后用 pyLDAvis 进行可视化。

def VisualizeLDA(model,corpus,dictionary):
	vis_data = gensimvis.prepare(model, corpus, dictionary)
	pyLDAvis.show(vis_data)

最后，我们需要定义一个函数，根据可供选择的主题的数量来直观地评估模型的质量。这将语料库、字典、要评估的主题的最大值数量（即语料库中的文档数量）和要评估的度量（默认情况下，复杂度）作为输入。需要执行以下两个步骤：

1. 通过迭代 $K$ 的几个值（即，主题的数量）来创建一个带有评估度量值的列表。
   • 对于 $K$ 的每个值，根据语料库 corpus 和字典 dic，主题模型被执行（gensim.models.ldamodel.LdaModel(…)）。
   • 根据所选度量，确定其困惑度（model.log_perplexity(…)）或连贯性（CoherenceModel(…)）的值并存储在列表中。
2. 从度量值列表中，绘制每个 $K$ 值与对应度量的值。

def showLDAMetricEvolution(corpus,dic,MaxDoc,metric="perp");
	descrip = {"perp":"Perplexity", "u_mass":"Coherence"}
	score = []
	list_k = list(range(2,MaxDoc))
	for K in list_k:
		model = gensim.models.ldamodel.LdaModel(corpus, numtopics=K, id2word = dic)
		if (metric == "perp"):
			value = model.log_perplexity(corpus)
		else:
			coherence = CoherenceModel(model=model, corpus=corpus, dictionary=dic, coherence="u_mass")
			value = coherence.get_coherence()
		score.append(value)
	plt.figure(figsize=(6, 6))
	plt.plot(list_k, score, '-o')
	plt.xticks(list_k)
	plt.xlabel(r'Number of Topics (K)')
	plt.ylabel(descrip[metric])

最后，加载语言模型，创建和预处理语料库，分配最大的文档数量和要生成的初步主题数量：

nlp = en_core_web_sm.load()

texts, _doc_id = CreateCorpus(PATH)
texts = PreProcessingWithNouns(texts)
MaxDoc = 7 
K = 3

但是，预处理的语料库（文本）需要转换为适合主题生成方法的格式。为此，我们必须遵循以下步骤：

1. 建立一个词典（corpora.Dictionary(…)）。从该类型的语料库中建立索引的单词列表 $(word,index)$。
2. 将文档语料库转换为 BoW 表示（doc2bow(text)）转换为对列表 $(wordindex,frequency)$。

dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]

一旦我们有了重新格式化的语料库，我们就可以使用 gensim.models.ldamodel 生成主题模型。使用生成的模型（modelLDA），我们可以显示 $K$ 个主题，每个主题都有最好的四个单词：

modelLDA = gensim.models.ldamodel.LdaModel(corpus, numtopics=K, id2word = dictionary)
print(modelLDA.print_topics(num_topics=K, num_words=4)

结果显示了以下四个主题（0-3）的主题分布及其估计的概率：

In[189]:print(modelLDA.print_topics(num_topics=K, num_words=4))

[(0, '0.014*"England" + 0.012*"Irons" + 0.010*"Stewart" + 0.010*"Moore"'),
 (1, '0.011*"season" + 0.010*"Klopp" + 0.009*"Flamengo" + 0.089*"slalom"'), 
 (2, '0.017*"Leslie" + 0.016*"year" + 0.013*"England" + 0.011*"time"')]

注意，我们之前假设 $k=4$。然而，我们不确定这是否是主题的最佳数量。为了直观地根据困惑度或连贯性度量来评估模型的质量，我们可以简单地调用我们的函数来可视化这两个度量的值的变化：

ShowLDAMetricEvolution(corpus, dictionary, MaxDoc, "perp")
ShowLDAMetricEvolution(corpus, dictionary, MaxDoc, "u_mass")

可视化结果如下所示：

您可以使用认为方便的两个指标中的任何一个。图中显示，$K=4$ 时达到的困惑度最低，而 $K=6$ 时达到的连贯性最高。

另一方面，我们可以以一种更直观的方式可视化我们的主题模型以进行视觉检查，因此对模型使用可视化函数 VisualizeLDA：

VisualizeLDA(modelLDA, corpus, dictionary)

显示以下图形界面（注：下图是博主绘制的，原文的图不清晰）：

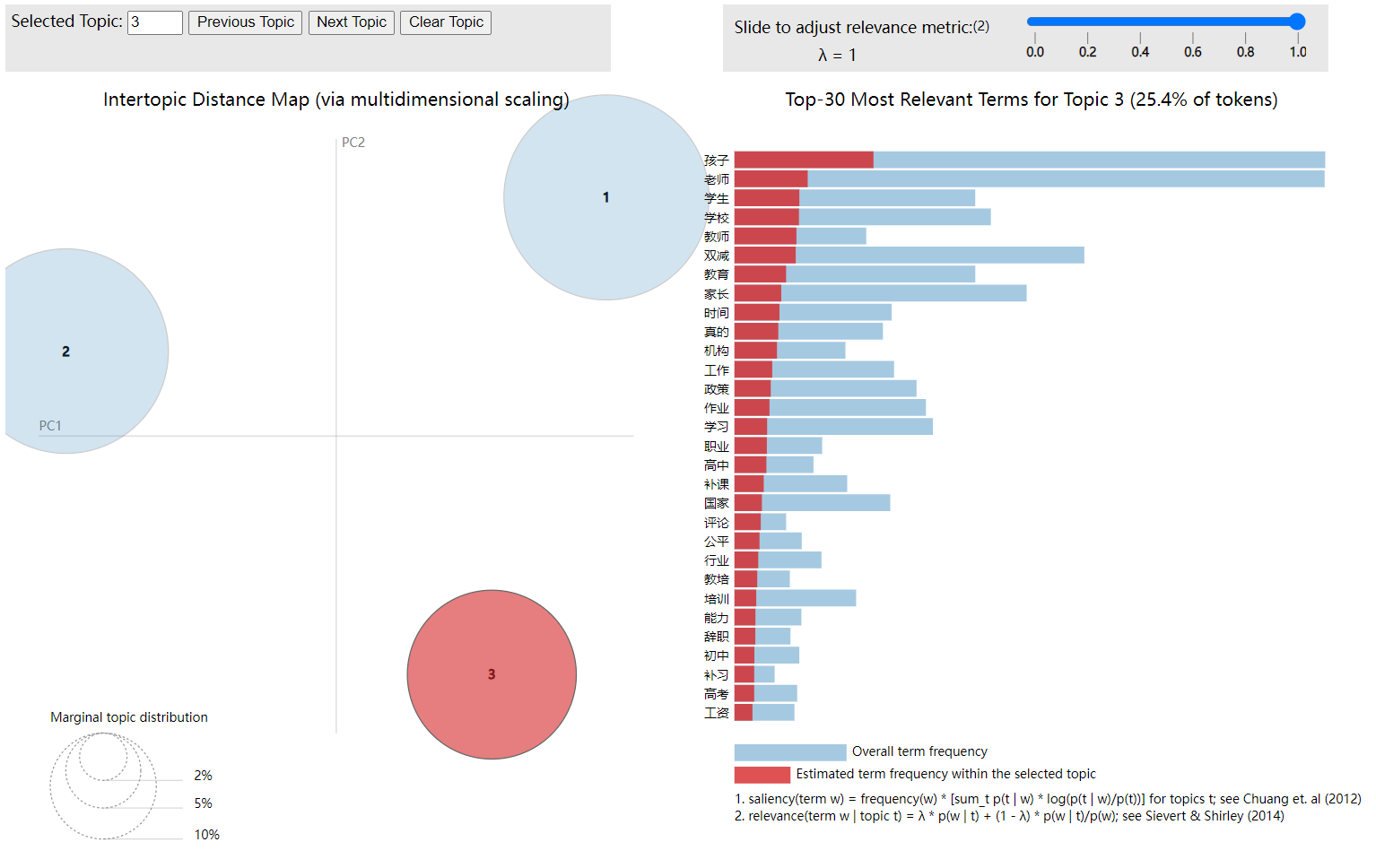
在左侧，可以看到通过多维尺度（Multidimensional Scaling，MDS）在一定距离上显示的主题，可以选择要显示的主题（以红色表示）。右侧显示了与每个主题（红色）相关的最佳的 $30$ 个词在总频率中的频率（浅蓝色）。

请注意，当 LDA 在一个语料库上运行时，一些单词会在整个语料库中频繁出现，因此根据它们在不同主题中的频率为 $p(w|k)$，它们会被确定为最佳单词。由于它们的 transversality（横向性 ？），它们不会有太大的相关性。为了解决这个问题，通常这个相对频率可以乘以一个与熵指数相关的相关因子 $\lambda$。这样，当 $\lambda =1$ 时，最好的单词是频率为 $p(w|k)$ 的单词；当 $\lambda <1$ 时，这意味着非常频繁的最佳单词会受到惩罚，所以它们的频率是：$p(w|k)\ast \lambda$。

---

本文译自书籍《Text Analytics：An Introduction to the Science and Applications of Unstructured Information Analysis》第 $8$ 章，主题建模（Topic Modeling）。