目录
Day - 1
896. 单调数列 - 简单ac
28. 找出字符串中第一个匹配项的下标 - KMP
1、kmp模板
2、java api
Day - 2
110. 平衡二叉树 - 递归
1、自顶向下 - 暴力
459. 重复的子字符串 - 暴力
Day - 3
150. 逆波兰表达式求值 - 栈 + 后缀表达式
66.加一 - 模拟
Day - 4
1367. 二叉树中的链表 - dfs 枚举
43. 字符串相乘 - 模拟乘法
Day - 1
896. 单调数列 - 简单ac
896. 单调数列
class Solution {
public boolean isMonotonic(int[] nums) {
boolean f1=false,f2=false;
for(int i=1;i<nums.length;i++)
if(nums[i]<nums[i-1]) f1=true;
else if(nums[i]>nums[i-1]) f2=true;
if(f1&&f2) return false;
return true;
}
}28. 找出字符串中第一个匹配项的下标 - KMP
28. 找出字符串中第一个匹配项的下标
1、kmp模板
【✓基础算法 2.4】KMP(完结)_Roye_ack的博客-CSDN博客
class Solution {
public:
int strStr(string ss, string pp) {
int n=ss.size(),m=pp.size();
int ne[m+1];
memset(ne,0,sizeof(ne));
string s=" "+ss;
string p=" "+pp;
//求next[]
for(int i=2,j=0;i<=m;i++)
{
while(j&&p[i]!=p[j+1]) j=ne[j];
if(p[i]==p[j+1]) j++;
ne[i]=j;
}
//kmp匹配
for(int i=1,j=0;i<=n;i++)
{
while(j&&s[i]!=p[j+1]) j=ne[j];
if(s[i]==p[j+1]) j++;
if(j==m) return i-m;
}
return -1;
}
};2、java api
class Solution {
public int strStr(String haystack, String needle) {
return haystack.indexOf(needle);
}
}Day - 2
110. 平衡二叉树 - 递归
110. 平衡二叉树
1、自顶向下 - 暴力
- 构造一个获取当前节点最大深度的方法 depth(root)
- 通过比较此子树的左右子树的最大高度差 abs(depth(root.left) - depth(root.right))来判断此子树是否是二叉平衡树
- 若树的所有子树都平衡时,此树才平衡
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null) return true;
return Math.abs(depth(root.left)-depth(root.right))<=1&&isBalanced(root.left)&&isBalanced(root.right);
}
public int depth(TreeNode root)
{
if(root==null) return 0;
return Math.max(depth(root.left),depth(root.right))+1;
}
}459. 重复的子字符串 - 暴力
459. 重复的子字符串
枚举每个子串n'的长度
class Solution {
public boolean repeatedSubstringPattern(String s) {
int n=s.length();
//因为子串至少重复一次,所以子串长度n'<=n/2
for(int i=1;i<=n/2;i++) //枚举n'串长度
if(n%i==0)
{
String t=s.substring(0,i);
String res="";
for(int j=0;j<n/i;j++) res+=t;
if(res.compareTo(s)==0) return true;
}
return false;
}
}Day - 3
150. 逆波兰表达式求值 - 栈 + 后缀表达式
150. 逆波兰表达式求值
思路:
后缀表达式:操作数在前边,操作符号在后边
- 遇到数字先入栈
- 遇到符号时,取出栈中两个数字,先出栈的为右操作数,后出栈的为左操作数
- 计算的结果再压入栈
- 最后栈剩下的元素即为结果
class Solution {
public int evalRPN(String[] tokens) {
int n=tokens.length;
Deque<Integer> stk=new LinkedList<>();
for(int i=0;i<n;i++)
{
String t=tokens[i];
if(t.equals("+")||t.equals("-")||t.equals("*")||t.equals("/"))
{
int n2=stk.pop(),n1=stk.pop();
switch(t)
{
case"+":stk.push(n1+n2);break;
case"-":stk.push(n1-n2);break;
case"*":stk.push(n1*n2);break;
case"/":stk.push(n1/n2);break;
default:
}
}else stk.push(Integer.parseInt(t));
}
return stk.pop();
}
}
66.加一 - 模拟
66. 加一
从个位开始遍历,如果此位为9,则+1进位变为0,前面一位+1后返回答案数组
如果所有位数均为9,则数组长度+1,首位为1
class Solution {
public int[] plusOne(int[] digits) {
for(int i=digits.length-1;i>=0;i--)
if(digits[i]==9) digits[i]=0;
else
{
digits[i]+=1;
return digits;
}
//如果所有位都是9 则长度+1
digits=new int[digits.length+1];
digits[0]=1;
return digits;
}
}Day - 4
1367. 二叉树中的链表 - dfs 枚举
1367. 二叉树中的链表
思路:
从根节点开始,遍历所有点,每次dfs都是以该点为起点查找是否有与链表匹配的路径
dfs中
- 如果链表遍历完,说明匹配成功
- 如果树遍历完,说明匹配失败
- 如果当前点值不相同,说明匹配失败
- 如果当前点值相同,则继续向下查找,左右只要有一条路满足即可
class Solution {
public boolean dfs(ListNode head,TreeNode e)
{
if(head==null) return true; //链表已经匹配完
if(e==null) return false; //二叉树访问到空节点
if(head.val!=e.val) return false;
return dfs(head.next,e.left)||dfs(head.next,e.right); //左右只要有一条匹配上就ok
}
public boolean isSubPath(ListNode head, TreeNode root) {
if(root==null) return false;
//从根节点开始向下枚举,以每一个节点为起点的路径,看是否与链表匹配
return dfs(head,root)||isSubPath(head,root.left)||isSubPath(head,root.right);
}
}43. 字符串相乘 - 模拟乘法
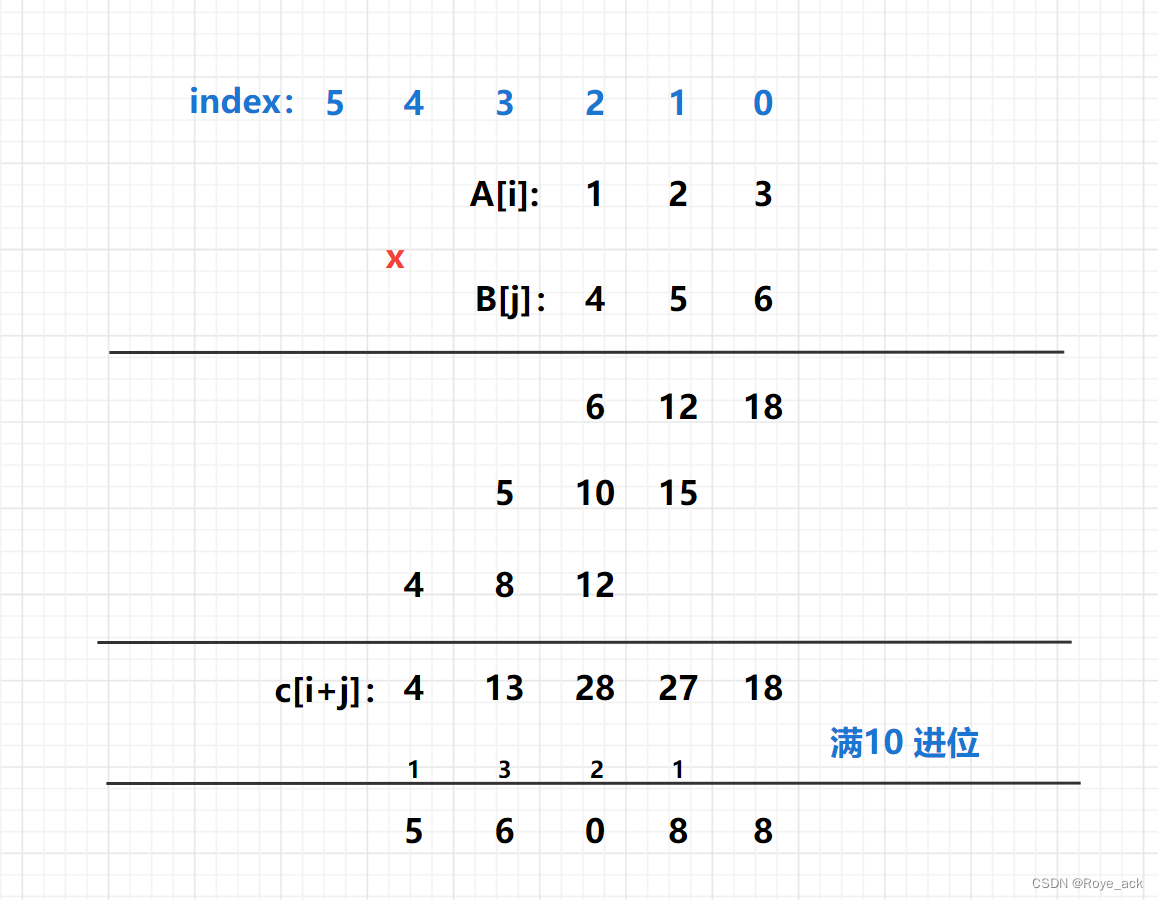
43. 字符串相乘
思路:
class Solution {
public String multiply(String num1, String num2) {
int n1=num1.length(),n2=num2.length();
int[] a=new int[n1],b=new int[n2];
for(int i=n1-1;i>=0;i--) a[n1-i-1]=num1.charAt(i)-'0'; //a[3,2,1]
for(int i=n2-1;i>=0;i--) b[n2-i-1]=num2.charAt(i)-'0'; //b[6,5,4]
int[] c=new int[n1+n2];
for(int i=0;i<n1;i++)
for(int j=0;j<n2;j++)
c[i+j]+=a[i]*b[j];
int t=0; //t为进位数
for(int i=0;i<c.length;i++)
{
t+=c[i];
c[i]=t%10;
t/=10;
}
int k=c.length-1;
while(k>0&&c[k]==0) k--; //去掉前导0
StringBuilder res=new StringBuilder();
//翻转
for(int i=k;i>=0;i--) res.append((char)(c[i]+'0'));
return res.toString();
}
}