目录

牛客DD1 连续最大和

解析代码

---

牛客DD1 连续最大和

连续最大和_牛客题霸_牛客网

---

解析代码

        本题是一个经典的动规问题，简称dp问题，但这个问题是非常简单的dp问题，而且经常会考察，所以一定要把这个题做会。本题题意很简单，就是求哪一段的子数组的和最大。 

状态转移方程： max( dp[ i ] ) = max( max( dp[ i -1 ] ) + arr[ i ] ,arr[ i ] )

        dp[i] 就是以数组下标为 i 的数做为结尾的最大子序列和，注意是以 i 为结尾，比如说现在有一个数组 {6,-3,-2,7,-15,1,2,2}，dp[2]就是以-2为结尾的，那么显然dp[2]的最大值就是1（6，-3，-2），dp[3]要以7结尾那么以7结尾的子序列最大和就是8（6，-3，-2，7）。现在我们开始细细品一下上面这个递推式，求dp[i] 的时候是不是有两种可能，要么就是像上面的dp[3]一样，dp[2]求出来是1了，再加上自己arr[3]是最大的，那么还有一种可能就是说如果dp[2]我求出来是-100，那如果我也是dp[2]+arr[3]的话是-93， 这时候 dp[2]反而是累赘，最大就是自己（因为前面定义了必须以i为结尾，也就说必须以7结尾）。

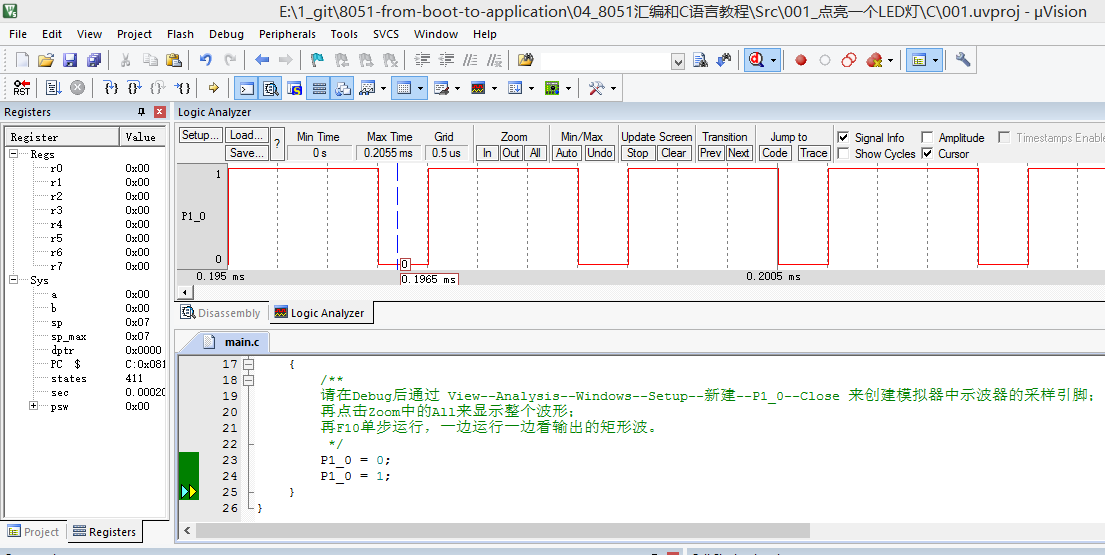
#include <climits>
#include <iostream>
#include <vector>
using namespace std;
int main()
{
	int n = 0;
	cin >> n;
	vector<int> arr(n);
	for (int i = 0; i < n; ++i)
	{
		cin >> arr[i];
	}
    int ret = arr[0];
    for (int i = 1; i < arr.size(); i++) 
    {
        arr[i] += max(arr[i - 1], 0);
        ret = max(ret, arr[i]);
    }
    /*
	int ret = -INT_MAX, sum = 0;
    for (int i = 0; i < n; ++i)
	{
		for (int j = i; j < n; ++j)
		{
			sum += arr[j];
			ret = max(ret, sum);
		}
		sum = 0;
	}
    */
	cout << ret;
	return 0;
}