【数据结构】探索排序的奥秘

news2024/9/22 11:40:13

若有不懂地方，可查阅我之前文章哦！

                   个人主页：小八哥向前冲~_csdn博客

                    所属专栏：数据结构_专栏

目录

排序的概念

几种排序方法介绍

冒泡排序

选择排序

插入排序

堆排序

向上调整建堆排序

向下调整建堆排序

希尔排序

快速排序

hoare版本快排

前后指针版本快排

非递归快排

归并排序

递归归并

非递归归并

扩展

计数排序

排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次 序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排 序算法是稳定的；否则称为不稳定的。

内部排序：数据元素全部放在内存中的排序。

外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不断地在内外存之间移动数据的排序

几种排序方法介绍

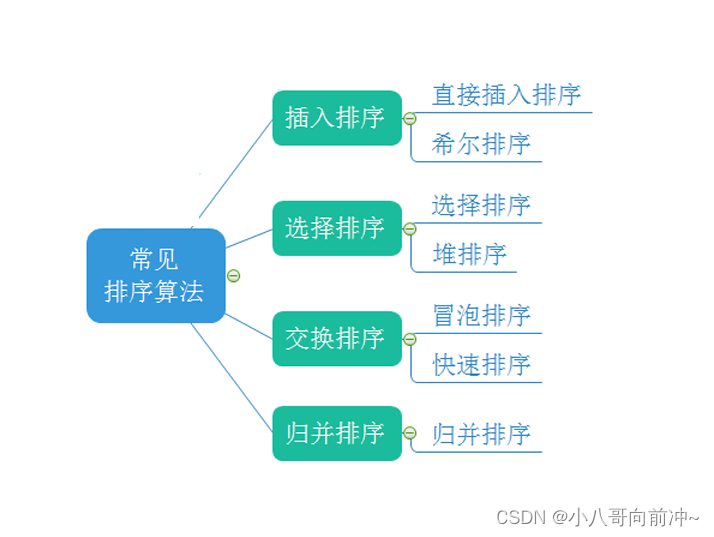
注意：下面各种排序将数组升序！

冒泡排序

冒泡排序相信你们都已经非常了解了！这里我们简单介绍一下就行！

有n个数，需要升序排列。我们只需要n-1趟排序，每趟排序将最大的排到了最后一个位置！

也就是说，每趟可以选出最大一个数且在最后一个位置上！

动画演示：

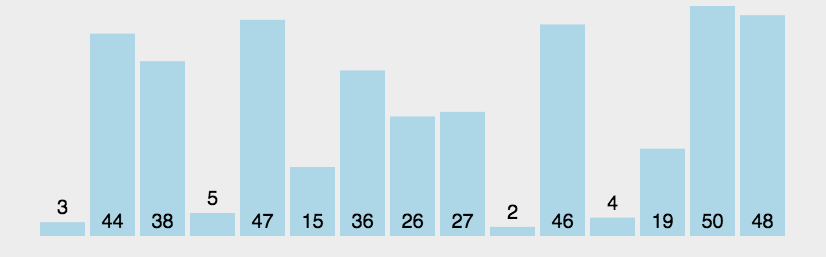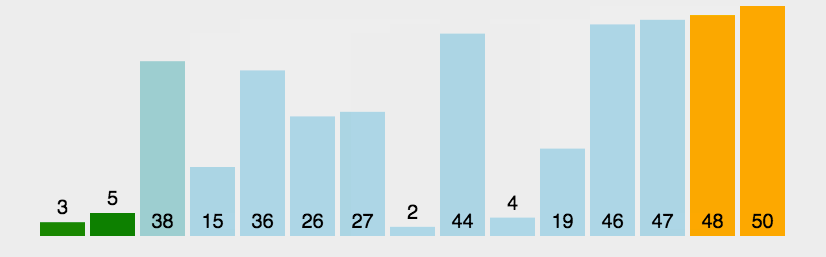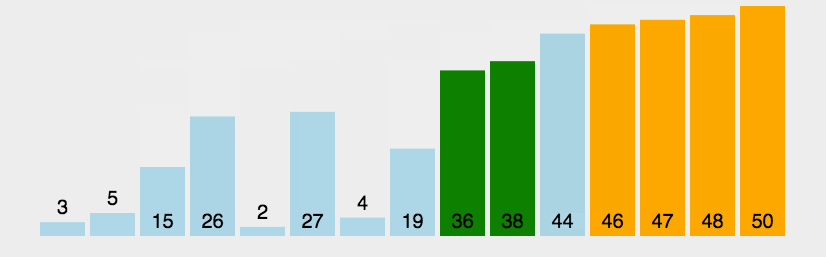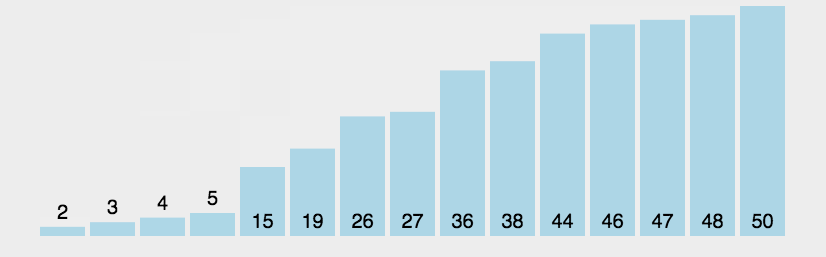
时间复杂度：o(N^2)

代码：

//交换
void Swap(int* p, int* q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;
}

//冒泡排序   o(N^2)
void BubbleSort(int* a, int n)
{
	for (int j = 0; j < n - 1; j++)
	{
		for (int i = 0; i < n - 1 - j; i++)
		{
			if (a[i] > a[i + 1])
			{
				Swap(&a[i], &a[i + 1]);
			}
		}
	}
}

选择排序

思路：

选择排序比较简单，选择——顾名思义，不断遍历数组，选择其中最小和最大的数，将最小数放在数组左侧，最大数放在数组右侧！

对于这个排序，我不做过多解释，比较简单！但是这里有一个小坑！

图：

代码：

void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int maxi = 0, mini = 0;
		for (int i = begin ; i <= end; i++)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		Swap(&a[mini], &a[begin]);
		//begin和maxi相等时，刷新maxi
		if (begin == maxi)
		{
			maxi = mini;
		}
		Swap(&a[maxi], &a[end]);
		begin++;
		end--;
	}
}

插入排序

插入排序动画演示：

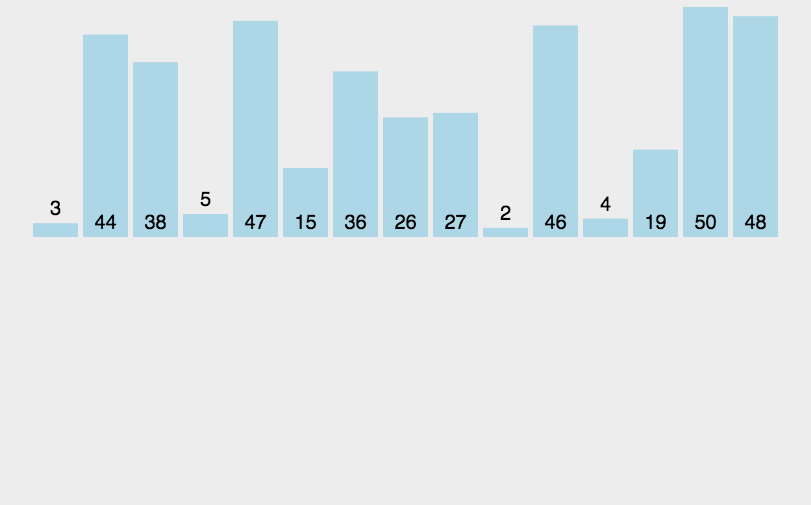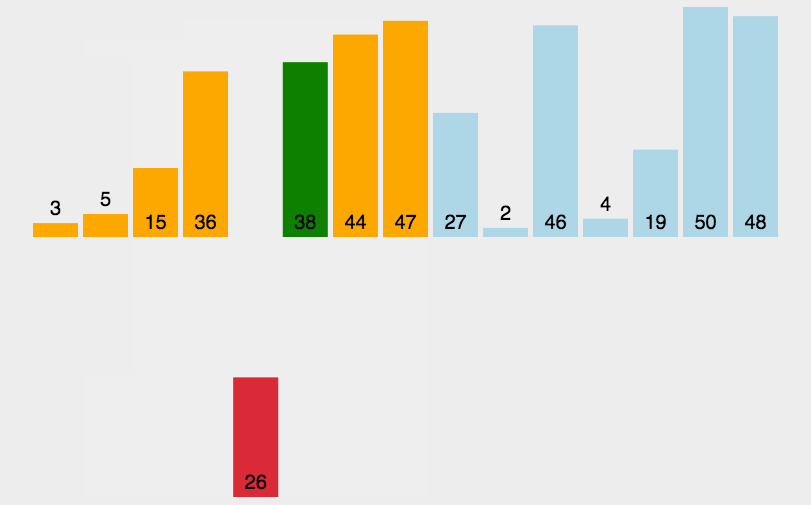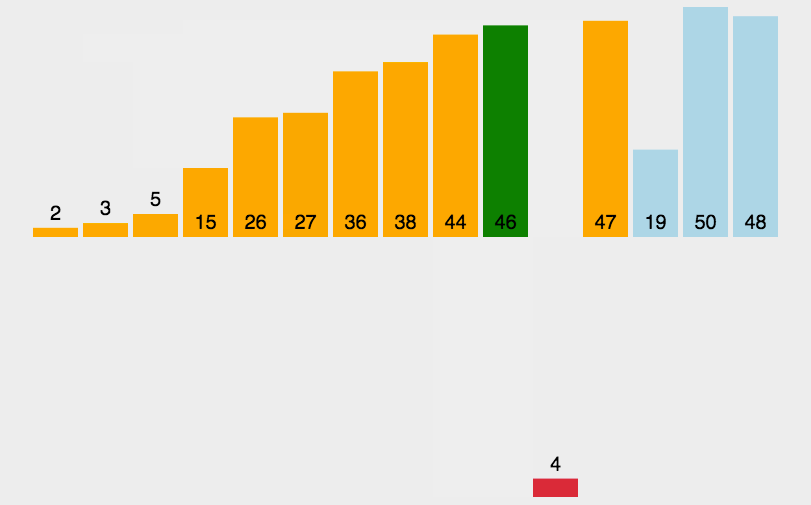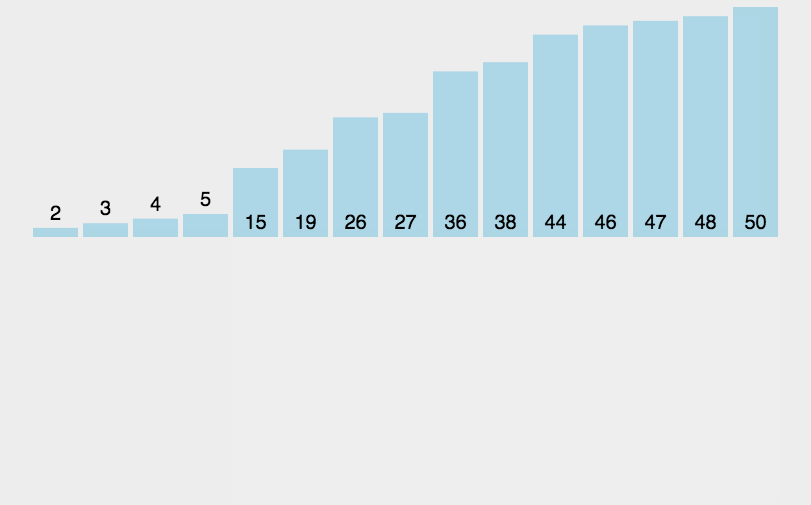
比如：要求升序，将一个一个数依次往前比较，比它大的往后移，知道比它小的数，再插进去！

时间复杂度：最坏情况-逆序-o(N^2)     最好情况-有序-o(N)

代码：

//插入排序
void Insert(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

堆排序

由于前俩章介绍了堆和二叉树，这里的堆排序不过多讲述，可翻阅我之前文章！

       传送门：CSDN--详解堆   

我们这里介绍俩种排序方法！

向上调整建堆排序

思路：

以将数组拍成升序为例，将数组中的数建成大堆，此时第一个数就是最大的数！再将第一个数和最后一个数交换，以此循环！

代码：

//向上调整
void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n&&a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[parent], &a[child]);
		}
		else
		{
			break;
		}
	}
}
//堆排序--向上调整-o(N*logN)
void HeapUpSort(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		AdjustUp(a, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

注意：时间复杂度——o(N*logN)

向下调整建堆排序

思路：

用向下调整的方法将数组调成大堆，那么第一个数就是数组中最大的数！然后将第一个数和数组最后一个数交换，以此循环交换！

代码：

//向下调整
void AdjustDown(int* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n&&a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[parent], &a[child]);
		}
		else
		{
			break;
		}
	}
}
//堆排序—向下调整建堆—o(N)
void HeapDownSort(int* a, int n)
{
	for (int i = (n - 1 - 1) / 2; i > 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[end], &a[0]);
		AdjustDown(a, end, 0);
		end--;
	}
}

希尔排序

先将数组里面的数分组，然后将分组好了的数排序，最后将整个数组利用插入排序进行最后的排序！

第一种代码：

//希尔排序   o(N^1.3)
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int j = 0; j < gap; j++)
		{
			for (int i = j; i < n - gap; i += gap)
			{
				int end = i;
				int tmp = a[end + gap];
				while (end >= 0)
				{
					if (a[end] > tmp)
					{
						a[end + gap] = a[end];
						end -= gap;
					}
					else
					{
						break;
					}
				}
				a[end + gap] = tmp;
			}
		}
	}
}

第二种代码：

//希尔排序   o(N^1.3)
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

快速排序

hoare版本快排

霍尔版本的快速排序动画演示：

思路：

先在这个数组中寻找一个参考值，将数组左边排成都比参考值小，数组右边排成都比参考值大！然后中间值将参考值交换。再将中间值左右边都这样循环往复操作，形成有序！

代码：

void Swap(int* q, int* p)
{
	int tmp = *q;
	*q = *p;
	*p = tmp;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int keyi = left;
	int begin = left, end = right;
	while (begin < end)
	{
		//右边找小
		while (begin<end && a[end]>a[keyi])
		{
			end--;
		}
		//左边找大
		while (begin < end && a[begin] < a[keyi])
		{
			begin++;
		}
		Swap(&a[begin], &a[end]);
	}
	Swap(&a[keyi], &a[begin]);
	keyi = begin;
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

但是这样写有一点瑕疵，我们可以近一步优化！

这段代码的“瑕疵”在：

  • 可能会栈溢出（递归太深）
  • 可以将后面递归排序进行优化

第一个瑕疵可以：当你取的参考值是数组里面最小的，那么就只会递归后面的n-1个数！这种情况是最有可能栈溢出（递归太深）！

我们可以进行三数取中优化！

第二个瑕疵可以：当一直递归排序时，数组过大非常适合取中快排，但是当数组过小，我们没有必要用快排排序，我们可以用插入排序！

优化代码：

void Swap(int* q, int* p)
{
	int tmp = *q;
	*q = *p;
	*p = tmp;
}

//三数取中
int GetMid(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[right])
	{
		if (a[midi] < a[left])
		{
			return left;
		}
		else if (a[midi] > a[right])
		{
			return right;
		}
		else
		{
			return midi;
		}
	}
	else
	{
		if (a[midi] > a[left])
		{
			return left;
		}
		else if (a[midi] < a[right])
		{
			return right;
		}
		else
		{
			return midi;
		}
	}
}
//插入排序
void Insort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	//三数取中优化
	int midi = GetMid(a, left, right);
	Swap(&a[left], &a[midi]);
	//小区间优化
	if ((right - left + 1) < 10)
	{
		Insort(a+left, right - left + 1);
	}
	else
	{
		int keyi = left;
		int begin = left, end = right;
		while (begin < end)
		{
			//右边找小
			while (begin<end && a[end]>a[keyi])
			{
				end--;
			}
			//左边找大
			while (begin < end && a[begin] < a[keyi])
			{
				begin++;
			}
			Swap(&a[begin], &a[end]);
		}
		Swap(&a[keyi], &a[begin]);
		keyi = begin;
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}

前后指针版本快排

前后指针版本的快排动画演示：

思路：

俩种方法大差不差，只是相比hoare版本，前后指针更好理解。俩种都是将数组分割成俩个小数组，进行排序！用的是双指针来分割交换数组！

代码：

//三数取中
int GetMid(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[right])
	{
		if (a[midi] < a[left])
		{
			return left;
		}
		else if (a[midi] > a[right])
		{
			return right;
		}
		else
		{
			return midi;
		}
	}
	else
	{
		if (a[midi] > a[left])
		{
			return left;
		}
		else if (a[midi] < a[right])
		{
			return right;
		}
		else
		{
			return midi;
		}
	}
}
int Partsort02(int* a, int left, int right)
{
	//三数取中优化
	int midi = GetMid(a, left, right);
	Swap(&a[left], &a[midi]);
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	//小区间优化
	if ((right - left + 1) < 10)
	{
		Insort(a+left, right - left + 1);
	}
	else
	{
		int keyi = Partsort02(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}

递归固然好，但它再好也逃不过栈溢出的风险！所以我们可以将递归改成非递归！

我们可以用栈来模拟递归思想从而变成非递归！

非递归快排

我们可以将区间入栈，再将区间出栈进行排序，分成俩组，再将这俩组分别入栈（后一组先入栈），前一组出栈排序，循环往复！

代码：

注意：里面的ST为栈结构，若有不懂可去我这篇文章---栈——CSDN-小八哥向前冲


//非递归
void QuickStack(int* a, int left, int right)
{
	ST st;
	STInit(&st);
	STpush(&st, right);
	STpush(&st, left);
	while (!STEmpty(&st))
	{
		//出栈取数据
		int begin = STtop(&st);
		STpop(&st);
		int end = STtop(&st);
		STpop(&st);
		//开始排序
		int keyi = Partsort02(a, begin, end);
		//排完一趟就入栈
		if (keyi + 1 < end)
		{
			STpush(&st, end);
			STpush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			STpush(&st, keyi - 1);
			STpush(&st, begin);
		}
	}
}

归并排序

递归归并

倘若有这样一个数组----它的前半部分有序，后半部分也有序（只不过整体不有序），就能利用归并将这个数组排成有序！

单趟理解：

那么使用归并排序，是不是应该先要前后部分分别有序呢？我们可以将数组一直二分下去归并排！

我们可以将它一直分开，直到不能分开了，就开始归并！

理解：

整体理解：

代码：

void _MergeSort(int* a, int* tmp, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int mid = (left + right) / 2;
	//分区间
	_MergeSort(a, tmp, left, mid);
	_MergeSort(a, tmp, mid + 1, right);
	//开始排
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int i = left;
	while (begin1<=end1 && begin2<=end2)//但凡有一个越界就跳出来
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	_MergeSort(a, tmp, 0, n - 1);
	free(tmp);
	tmp = NULL;
}

时间复杂度：N*logN

非递归归并

非递归思路：

那么如何将递归方式改成非递归呢？一定要区别归并和快排，快排是先排序再分，归并是先分再排！快排相当于是二叉树里面的前序，而归并相当于是后序！

这里利用栈不好实现，我们可以另辟蹊径！

既然不好实现分组，那我们可以进行手动分组，然后进行归并！

理解：

代码：

void MergeSortNon(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc faild !");
		return;
	}
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//第二组完全越界了，这组就不用归并了
			if (begin2 >= n)
			{
				break;
			}
			//第一组没越界，第二组部分越界，需要进行修正再归并
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)//但凡有一个越界就跳出来
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));
		}
		gap *= 2;
	}
	free(tmp);
	tmp = NULL;
}

这里解释一下为什么需要归并一部分复制一部分：

如果后部分越界了，就不会归并，那么tmp数组里面就没有没归并的数，只有归并了的数，如果是全部归并了再去复制一份的话，就直接覆盖了原来就有的数值！所以归并一部分再复制一部分是再好不过的选择！

扩展

计数排序

计数排序和其他排序方法截然不同，它摒弃了以往的比较大小的方法，转化成计数的方法！

我们上图比较好理解：

代码：

void CountSort(int* a, int n)
{
	int max = a[0], min = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;
	int* count = (int*)calloc(range,sizeof(int));
	if (count == NULL)
	{
		perror("malloc faild!");
		return;
	}
	//开始计数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	//开始往回写
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
	free(count);
	count = NULL;
}

这里代码有个小细节：

开辟空间不用malloc,而用calloc，是因为我们新开辟的数组里面元素都要置0，再进行计数，而calloc开辟完了空间就会将数组元素全部置0！

全部排序总结

好了，今天的分享就到这里，我们在C++不见不散！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1943342.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【数学建模】——前沿图与网络模型：新时代算法解析与应用

【数学建模】——前沿图与网络模型：新时代算法解析与应用

目录 1.图与网络的基本概念 1. 无向图和有向图 2. 简单图、完全图、赋权图 3. 顶点的度 4. 子图与图的连通性 2.图的矩阵表示 1. 关联矩阵 2. 邻接矩阵 3.最短路问题 1.Dijkstra 算法 2.Floyd 算法 4.最小生成树问题 1.Kruskal 算法 2.Prim 算法 5.着色问题 6.…
阅读更多...
【AI大模型】程序员AI的未来——Copilot还是Claude3.5 Sonnet？

【AI大模型】程序员AI的未来——Copilot还是Claude3.5 Sonnet？

近期&#xff0c;Anthropic发布了Claude 3.5 的“大杯”模型 —— Claude 3.5 Sonnet&#xff01; 这次发布的 Sonnet 代表意大利的“十四行诗”&#xff0c;结构复杂&#xff0c;在智能水平、功能多样性和处理能力上都有所提升&#xff0c;能够应对更复杂的认知任务&#xff…
阅读更多...
进程与进程函数

进程与进程函数

目录 进程与程序 1.1进程是什么 1.2程序&#xff0c;进程之间的关系 1.3进程的生存环境 1.4进程的状态转换 1.5关于内核层与用户层 1.6保存和恢复处理器现场 进程原语 2.1fork() ​编辑 2.1.1父子进程的继承 2.1.2父子进程共享fork()栈帧 2.1.3打印进程id和父进程i…
阅读更多...
【OpenREALM学习笔记：14】单目视觉SLAM方法在UAV影像上重建三维地形的思考

【OpenREALM学习笔记：14】单目视觉SLAM方法在UAV影像上重建三维地形的思考

最近在学习SLAM技术与测绘三维影像重建的相关知识&#xff0c;结合自己的感受&#xff0c;撰写一下对于单目视觉SLAM利用无人机影像重建三维地形的一些看法。 1. 单目视觉SLAM系统在三维地形重建中所面临的挑战有哪些&#xff1f; 单目视觉SLAM众所周知的一个问题是&#xff…
阅读更多...
C# 委托函数 delegate

C# 委托函数 delegate

在C#中&#xff0c;委托&#xff08;Delegate&#xff09;是一种特殊的类型&#xff0c;它可以持有对方法的引用。 委托是实现事件的基础。事件本质上是多播委托&#xff0c;允许多个方法被触发 委托允许你将方法作为参数传递给其他方法&#xff0c;或者将方法作为返回值从方法…
阅读更多...
feed流（投喂）

feed流（投喂）

1、拉模式&#xff1a; 优缺点&#xff1a;节省空间&#xff0c;只存一份&#xff0c;赵六在需要的时候直接去读。延迟高&#xff0c;耗时长。如果关注的人多的话&#xff0c;就会一次性拉取的很大&#xff0c;造成拥塞。 2、推模式 优缺点&#xff1a;延迟低&#xff0c;耗时少…
阅读更多...
嵌入式C++、STM32、树莓派4B、OpenCV、TensorFlow/Keras深度学习：基于边缘计算的实时异常行为识别

嵌入式C++、STM32、树莓派4B、OpenCV、TensorFlow/Keras深度学习：基于边缘计算的实时异常行为识别

1. 项目概述 随着物联网和人工智能技术的发展,智能家居安全系统越来越受到人们的关注。本项目旨在设计并实现一套基于边缘计算的智能家居安全系统,利用STM32微控制器和树莓派等边缘设备,实时分析摄像头数据,识别异常行为(如入侵、跌倒等),并及时发出警报,提高家庭安全性。 系…
阅读更多...
内存卡损坏读不出怎么修复？内存卡数据恢复的7个方法请收好！

内存卡损坏读不出怎么修复？内存卡数据恢复的7个方法请收好！

当面对内存卡损坏、无法读取数据的困扰时&#xff0c;许多人会感到焦虑和困惑。尤其是当这些卡中存储着珍贵的照片、视频或文件时&#xff0c;这种困扰更显得令人不安。您是否也曾因内存卡损坏而无法显示照片或遭遇需要格式化的提示而感到困扰&#xff1f;在我们日常的生活中&a…
阅读更多...
power bi文本,截取及查找函数

power bi文本,截取及查找函数

power bi文本,截取及查找函数 1. 文本函数1.concatenate函数2. exact 函数3. find函数4. search函数 2. 截取函数1. fixed 函数2. 大小写转换3. trim函数4.rept函数5. replace 函数6. substitute函数 3. 查找匹配函数1 contains函数2. treatas 函数3. ContainsString函数4. Con…
阅读更多...
GPT模型为什么能生成有意义的文本

GPT模型为什么能生成有意义的文本

GPT模型的底层&#xff0c;其实是谷歌团队推出的Transformer模型。但是在GPT-3出现之前&#xff0c;大家一直对它没有多少了解。直到它的参数数量突破1750亿个的时候&#xff0c;它才建立起一个庞大的神经网络&#xff0c;这个神经网络最突出的特点是大数据、大模型和大计算。其…
阅读更多...
宠物经济纵深观察：口红效应显著，呈可持续发展态势

宠物经济纵深观察：口红效应显著，呈可持续发展态势

七月以来&#xff0c;全国各地陆续开启高温模式。和人一样&#xff0c;“毛孩子们”同样也难耐高温&#xff0c;由此&#xff0c;围绕猫猫狗狗的“宠物经济”迅速升温&#xff0c;宠物冰垫、宠物饮水机、宠物烘干机......一系列宠物单品掀起夏日消费热潮。 就在几天前&#xf…
阅读更多...
mysql的主从复制和读写分离：

mysql的主从复制和读写分离：

mysql的主从复制和读写分离&#xff1a; 主从复制 面试必问&#xff1a;主从复制的原理 主从复制的模式&#xff1a; 1、mysql的默认模式&#xff1a; 异步模式 主库在更新完事务之后会立即把结果返回给从服务器&#xff0c;并不关心从库是否接受到&#xff0c;以及从库是…
阅读更多...
汽车研发项目管理系统排行榜：五大热门汽车项目管理系统推荐

汽车研发项目管理系统排行榜：五大热门汽车项目管理系统推荐

汽车研发项目管理软件在汽车制造行业中扮演着至关重要的角色&#xff0c;本文介绍了五款在汽车及零部件领域专业的项目管理软件。 一、 奥博思 PowerProject 企业级项目管理系统 奥博思 PowerProject 项目管理系统&#xff08;支持项目管理、项目集管理、项目组合管理三位一体…
阅读更多...
LLM之RAG理论（十二）| RAG和Graph RAG对比

LLM之RAG理论（十二）| RAG和Graph RAG对比

最近Graph RAG非常火&#xff0c;它来自微软的一篇论文《From Local to Global: A Graph RAG Approach to Query-Focused Summarization》&#xff0c;论文地址&#xff1a;https://arxiv.org/pdf/2404.16130。本文将对RAG 和 Graph RAG在架构和成本方面做简要分析。 一、RAG …
阅读更多...
家里灰尘多又不想打扫。教你一招，省时省事，除尘很轻松

家里灰尘多又不想打扫。教你一招，省时省事，除尘很轻松

出差半个月前&#xff0c;我住在新装修的房子里两周。在新餐桌上铺了一块桌布&#xff0c;结果一周后布上就积了一层灰尘。而且&#xff0c;那些夜里&#xff0c;我经常听到妻子剧烈咳嗽&#xff0c;令人担心。她有中度肺部疾病&#xff0c;平时非常注意卫生&#xff0c;每天都…
阅读更多...
mysql高阶语句：

mysql高阶语句：

mysql高阶语句&#xff1a; 高级语法的查询语句&#xff1a; select * from 表名 where limitsdistinct 去重查询like 模糊查询 排序语法&#xff1a;关键字排序 升序和降序 默认的排序方式就是升序 升序&#xff1a;ASC 配合order by语法 select * from 表名…
阅读更多...
大模型应用—大模型赋能搜索

大模型应用—大模型赋能搜索

大模型赋能搜索 AI正在改变搜索体验，使其对我们来说更加智能、个性化和高效。 你可能会想，“但是谷歌已经足够好了！”首先，谷歌的搜索相关性和个性化是有代价的，那么跨不同媒体类型的搜索呢？对于最相关的信息格式，甚至是自动化某些任务，比如抓取网站、索引内容和搜索…
阅读更多...
因为很会用工具，拿下了很多客户！

因为很会用工具，拿下了很多客户！

作为一名想要得到更多业绩的打工人&#xff0c;能提高工作效率的工具一定要拥有&#xff01; 今天&#xff0c;就给大家分享一个职场必备的提效神器&#xff0c;一起来看看它都有哪些功能吧&#xff01; 1、多渠道客源 它可以从多个渠道去获取你想要的客户资源&#xff0c;无…
阅读更多...
CSS画边框线带有渐变线和流光边框实例

CSS画边框线带有渐变线和流光边框实例

流光边框css流光边框动画效果_哔哩哔哩_bilibili流光边框css流光边框动画效果_哔哩哔哩_bilibili纯CSS写一个动态流水灯边框的效果&#xff5e;_哔哩哔哩_bilibili荧光边框CSS 动画发光渐变边框特效_哔哩哔哩_bilibili [data-v-25d37a3a] .flow-dialog-custom {background-col…
阅读更多...
简单使用SpringMVC写一个图书管理系统的登入功能和图书展示功能

简单使用SpringMVC写一个图书管理系统的登入功能和图书展示功能

准备好前端的代码 这里已经准备好了前端的代码&#xff0c;这里仅仅简单的介绍登入功能&#xff0c;和展示图书列表的功能。 如图&#xff1a; 如上图所示&#xff0c;这里的前端代码还是比较多的&#xff0c;在这里我介绍&#xff0c;login.html还有book_list.html这两个。 l…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023