$题意：给定两个$ $01$ $字符串$ $a$ $和$ $b$ ，$每次操作可选择字符串$ $a$ $上的数字反转$，$即：0$ $->1$ 或者 $1$ $->0。$$每个位上操作的$ 概率相同 $即每个位上操作的概率都是1/n$ ，$现问将字符串a翻转成b的期望步数是多少。$

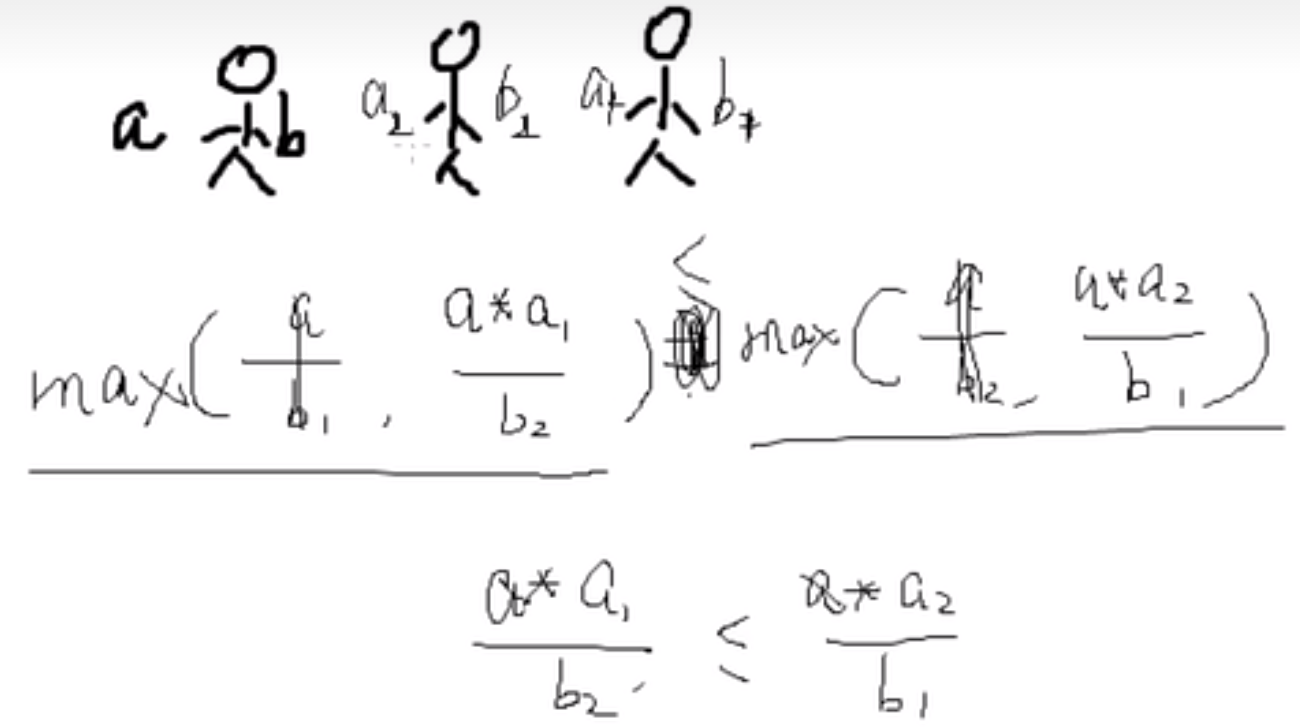
$公式推导：$

$参考代码：$

#include<bits/stdc++.h>
using namespace std;
#define int long long 
#pragma GCC optimize(3)
typedef pair<int,int>PII;
#define pb push_back
const int N = 1e6+10;
const int mod = 998244353;
int inv[N];
int c[N],d[N];//kx+b
int qmi(int a,int b){
    int res=1;
    while(b){
        if(b&1)res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}
void cf(){
    int sum=0;
    int n;
    cin>>n;
    string a,b;
    cin>>a>>b;
    for(int i=0;i<a.size();i++){
        if(a[i]!=b[i])sum++;
    }
    c[0]=d[0]=d[1]=0;
    c[1]=1;
    for(int i=2;i<=n;i++){
        c[i] = (c[i-1]*n-c[i-2]*(i-1))%mod*inv[n-i+1]%mod;
        d[i] = (d[i-1]*n-d[i-2]*(i-1)-n)%mod*inv[n-i+1]%mod;
    }
    int dp1=(1+d[n-1]-d[n])*qmi(c[n]-c[n-1],mod-2)%mod;
    int ans=(c[sum]*dp1+d[sum])%mod;
    if(ans<0)ans+=mod;
    cout<<ans<<endl;
    return ;
}
signed main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    inv[1]=1;
    for(int i=2;i<N;i++){//O(n)线性求区间逆元
        inv[i]=mod-mod/i*inv[mod%i]%mod;
    }
    int _=1;
    cin>>_;
    while(_--){
        cf();
    }
    return 0;
}