蒙特卡罗大部分改概念和方法不依赖空间的维度，可以先讨论一维情况下粒子的蒙特卡罗输运。

单能粒子输运的玻尔兹曼方程可以写为：

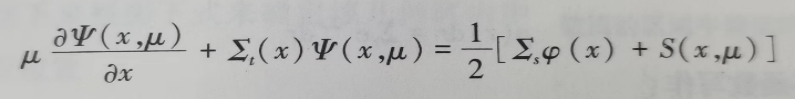
仅考虑散射和吸收

Et=Es+Ea

吸收意味着粒子生命周期的终结。

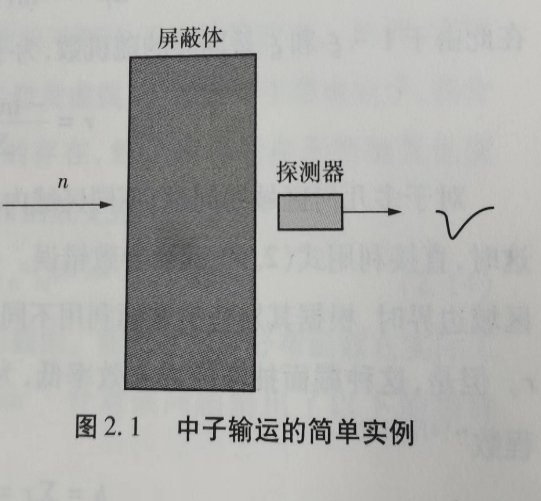
图2.1示例：通过蒙特卡罗方法确定目标几何体内外的中子分布、传输率或者中子的反射率。

有三个随机过程需要考虑：

1平均自由程

2反应类型：散射或者吸收

3散射角：如果发生反应并且反应过程为散射

平均自由程的确定 ：

粒子发生反应前自由运动的路程为自由程。

一个粒子自由运动一段路程 r，然后在接下来dr发生反应的概率是多少？

辐射物理理论推导出：运动路程 r 内不发生反应的概率为e ^-Etr，在dr内发生碰撞的概率为Etdr。联合概率为：p(r)(dr)=Et e^-Etr Dr

解运动路程为：Etr=-ln(1-$)

多几何区域：不同区域的材料不同，Et不再是常数.

解决办法：当粒子到达新的几何区域边界时，根据其对应的截面利用不同的随机数，从新的起点进行抽样给出r，截面抽样效率低，于是引入“平均自由程”

反应种类确定 ：

简单的离散型平均分布随机数

散射角的选择取：

单能中子的输运理论：

散射微分截面为Es（Q->Q'）dQ'

物理意义为沿Q‘方向运动的粒子在单位路程被散射在Q’附近dQ‘的概率

微分截面只依赖与散射角，也就是入射方向与散射方向的夹角。

输运的起始和终止：

使用蒙特卡罗方法对某一粒子进行输运应该有一个开始跟踪的时刻Tstart和一个终止跟踪的时刻Tend。在此时间段内粒子的状态和相互作用都被考虑，这个时间段称为粒子跟踪的生命周期。

通常选为该载能粒子从放射源产生的时间或粒子经过某特殊位置（如束流的焦平面）的时间。

终止粒子输运的时间由以下条件决定：

1粒子飞出所建立的几何空间模型之外

2粒子经过一系列物理过程被介质原子核吸收,比如伽马光子发生的光电效应

或者改变了存在形式，产生了新的次级粒子

3粒子没有消亡和飞出模型，但后续的物理过程不起关键作用了。

判断依据有

a粒子的动能低于某一能量下限,沉积到介质中

b在使用了减小方差的蒙特卡罗技巧后，粒子的权重小于阈值，将使用俄罗斯轮盘赌方法终止粒子的输运。

c粒子的飞行时间或者飞行路程等达到某一上限，防止计算资源被过度消耗