🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎人工智能和前端开发。
🦅个人主页：@逐梦苍穹
📕所属专栏：人工智能
🌻gitee地址：xzl的人工智能代码仓库
✈ 您的一键三连，是我创作的最大动力🌹

1、简介

本文目标：掌握梯度计算
先补充一篇我的文章，关于向量的计算方式：https://xzl-tech.blog.csdn.net/article/details/140563909

---

自动微分（Automatic Differentiation, Autograd）是计算梯度的强大工具，广泛应用于机器学习，特别是深度学习模型的训练过程中。
在PyTorch中，Autograd模块通过记录张量的操作并自动计算梯度，极大地简化了模型的优化过程。

1.1、基本概念

1. 张量（Tensor）：
   • PyTorch中的张量是自动微分的基础数据结构。每个张量都有一个属性 requires_grad，它指示是否需要计算该张量的梯度。
   • 张量的 grad 属性用于存储计算得到的梯度。
2. 计算图（Computational Graph）：
   • Autograd的核心是动态计算图，每次进行操作时都会动态地构建计算图。计算图的节点表示张量，边表示操作。
   • 在反向传播过程中，Autograd沿着计算图从输出节点到输入节点计算梯度。
3. 反向传播（Backpropagation）：
   • 反向传播是一种计算梯度的算法，通过链式法则（链式求导法则）逐层计算梯度。

自动微分（Autograd）模块对张量做了进一步的封装，具有自动求导功能。自动微分模块是构成神经网络训练的必要模块，在神经网络的反向传播过程中，Autograd 模块基于正向计算的结果对当前的参数进行微分计算，从而实现网络权重参数的更新。

1.2、基本原理

1.2.1、自动微分

在PyTorch中，自动微分通过记录对张量的所有操作来实现。当调用反向传播函数backward()时，Autograd根据链式法则自动计算所有梯度。
链式法则：
设 $y=f(u)$ 且 $u=g(x)$ ，根据链式法则，函数$(y)$对 $(x)$ 的导数为：
$[\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}]$
在计算图中，Autograd通过遍历所有节点，按此法则计算梯度。

1.2.2、梯度

梯度 (Gradient)

梯度是多变量函数的偏导数向量，它表示函数在各个变量方向上的变化率。
在数学上，给定一个多变量函数$(f(x_1,x_2,...,x_n))$，它的梯度是一个向量，
其分量是函数对每个变量的偏导数：$[\nabla f=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...,\frac{\partial f}{\partial x_n}\right)]$
梯度向量指向函数值增长最快的方向，其长度表示函数值增长最快的速率。

1.2.3、梯度求导

梯度求导 (Gradient Calculation)

梯度求导是计算函数在特定点的梯度向量的过程。对于机器学习和深度学习中的目标函数（通常是损失函数），我们通过梯度求导来了解参数变化对目标函数的影响，从而调整参数以最小化目标函数。
一维函数的导数：
对于一维函数$(f(x))$，导数 $(f^{\prime }(x))$表示函数在点$(x)$处的变化率。
数学上，导数定义为：$[f^{\prime }(x)={\lim }_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}]$
多维函数的梯度：
对于多维函数$(f(x_1,x_2,...,x_n))$，梯度是各个方向上的导数组成的向量：
$[\nabla f=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...,\frac{\partial f}{\partial x_n}\right)]$

1.2.4、梯度下降法

梯度下降法 (Gradient Descent)

梯度下降法是一种优化算法，通过逐次调整参数以最小化目标函数。具体步骤如下：

1. 初始化参数$(\theta )$。
2. 计算当前参数的梯度$(\nabla f(\theta ))$。
3. 更新参数： $(\theta =\theta -\alpha \nabla f(\theta ))$，其中$(\alpha )$是学习率。
4. 重复步骤2和3，直到收敛。

1.2.5、张量梯度举例

标量对张量的梯度：
假设有一个标量函数$(f)$作用于张量$(T)$，梯度$(\nabla f)$是一个与$(T)$具有相同维度的张量，
其元素是$(f)$对 $(T)$中每个元素的偏导数：$[(\nabla f)ijk...=\frac{\partial f}{\partial Tijk...}]$
例子：张量的平方和函数：

考虑一个张量的平方和函数：$[f(T)={\sum }_{i,j,k,...}{T}_{ijk...}^2]$
对张量 ( T ) 的每个元素求导：$[\frac{\partial f}{\partial T_{ijk...}}=2T_{ijk...}]$
所以，梯度是：$[\nabla f=2T]$

在实际应用中，通常需要对更复杂的函数计算梯度，如神经网络的损失函数对模型参数的梯度。这时，梯度计算不仅限于简单的平方和函数，而是涉及到复杂的链式求导。
例子：神经网络的反向传播

考虑一个简单的神经网络前向传播：$[y=\sigma (Wx+b)]$
其中$(\sigma )$是激活函数，$(W)$ 是权重矩阵，$(x)$ 是输入，$(b)$是偏置。
假设损失函数是均方误差：$[L=\frac{1}{2}(y-\hat{y}{)}^2]$
我们需要计算损失函数对权重矩阵和偏置的梯度。

1.3、Autograd的高级功能

1. 梯度累积：
   • 默认情况下，调用 backward() 时，梯度会累积到张量的 grad 属性中。可以通过 x.grad.zero_() 来清零梯度。
2. 非标量输出的梯度：
   • 当输出不是标量时，可以传递一个和输出形状相同的权重张量作为 backward() 的参数，用于计算加权和的梯度。
3. 禁用梯度计算：
   • 在不需要梯度计算的情况下，可以使用 torch.no_grad() 或 with torch.no_grad(): 来临时禁用梯度计算，从而提高性能和节省内存。

我们使用 backward 方法、grad 属性来实现梯度的计算和访问.

2、梯度基本计算

2.1、单标量梯度

import torch
# 1. 单标量梯度的计算
# y = x**2 + 20
def test01():
    # 定义需要求导的张量
    # 张量的值类型必须是浮点类型
    x = torch.tensor(10, requires_grad=True, dtype=torch.float64)
    print(x)
    # 变量经过中间运算
    f = x ** 2 + 20
    print(f)
    # 自动微分
    f.backward()
    # 打印 x 变量的梯度
    # backward 函数计算的梯度值会存储在张量的 grad 变量中
    print(x.grad)
    print(x)

程序运行结果：

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py 
tensor(10., dtype=torch.float64, requires_grad=True)
tensor(120., dtype=torch.float64, grad_fn=<AddBackward0>)
tensor(20., dtype=torch.float64)
tensor(10., dtype=torch.float64, requires_grad=True)

Process finished with exit code 0

解释：

1. 张量 x 的初始值： tensor(10., dtype=torch.float64, requires_grad=True) 表示 x 的初始值是10，并且它的梯度计算已被启用。
2. 中间变量 f 的值： tensor(120., dtype=torch.float64, grad_fn=<AddBackward0>) 表示 f 的计算结果是120，即$(10^2+20)$。
3. 梯度值 x.grad： tensor(20., dtype=torch.float64) 表示 f 对 x 的梯度是20，即$\frac{d}{dx}(x^2+20)=2x=2\times 10$。
4. 张量 x 的值保持不变： tensor(10., dtype=torch.float64, requires_grad=True) 再次确认 x 的值保持为10。

2.2、单向量梯度的计算

# 2. 单向量梯度的计算
# y = x**2 + 20
def test02():
    # 定义需要求导张量
    x = torch.tensor([10, 20, 30, 40], requires_grad=True, dtype=torch.float64)
    print(x)
    # 变量经过中间计算
    f1 = x ** 2 + 20
    print(f1)
    # 注意:
    # 由于求导的结果必须是标量
    # 而 f 的结果是: tensor([120., 420.])
    # 所以, 不能直接自动微分
    # 需要将结果计算为标量才能进行计算
    print(f1.mean())
    f2 = f1.mean()  # f2 = 1/2 * x
    # 自动微分
    f2.backward()
    # 打印 x 变量的梯度
    print(x.grad)

输出：

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py 
tensor([10., 20., 30., 40.], dtype=torch.float64, requires_grad=True)
tensor([ 120.,  420.,  920., 1620.], dtype=torch.float64,
       grad_fn=<AddBackward0>)
tensor(770., dtype=torch.float64, grad_fn=<MeanBackward0>)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)

Process finished with exit code 0

解释：

函数 f1 的定义：$[f_{1i}=x_i^2+20]$
f2 是 f1 的均值：$[f2=\frac{1}{4}{\sum }_{i=1}^4{f}_{1i}]$
因此，f2 对 x_i 的偏导数为：$[\frac{\partial f2}{\partial x_i}=\frac{1}{4}\frac{\partial f_{1i}}{\partial x_i}=\frac{1}{4}\cdot 2x_i=\frac{1}{2}{x}_i]$
所以，f2 对 x 的梯度 x.grad 为每个元素的一半：$[x.grad=\left[\frac{1}{2}\cdot 10,\frac{1}{2}\cdot 20,\frac{1}{2}\cdot 30,\frac{1}{2}\cdot 40\right]=[5,10,15,20]]$

2.3、多标量梯度计算

# 3. 多标量梯度计算
# y = x1 ** 2 + x2 ** 2 + x1*x2
def test03():
    # 定义需要计算梯度的张量
    x1 = torch.tensor(10, requires_grad=True, dtype=torch.float64)
    x2 = torch.tensor(20, requires_grad=True, dtype=torch.float64)
    print(x1, x2)
    # 经过中间的计算
    y = x1 ** 2 + x2 ** 2 + x1 * x2
    print(y)
    # TODO y已经是标量, 无需转换
    # 自动微分
    y.backward()
    # 打印两个变量的梯度
    print(x1.grad, x2.grad)

输出：

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py 
tensor(10., dtype=torch.float64, requires_grad=True) tensor(20., dtype=torch.float64, requires_grad=True)
tensor(700., dtype=torch.float64, grad_fn=<AddBackward0>)
tensor(40., dtype=torch.float64) tensor(50., dtype=torch.float64)

Process finished with exit code 0

解释-梯度计算细节：

1. 定义函数 $(y)$：$[y=x_1^2+x_2^2+x1\cdot x2]$
2. 计算 $(y)$：$[y=102+202+10\cdot 20=100+400+200=700]$
3. 计算梯度 ($\frac{\partial y}{\partial x1}$)：$[\frac{\partial y}{\partial x1}=2x1+x2=2\cdot 10+20=20+20=40]$
4. 计算梯度 ($\frac{\partial y}{\partial x2}$)：$[\frac{\partial y}{\partial x2}=2x2+x1=2\cdot 20+10=40+10=50]$

2.4、多向量梯度计算

# 4. 多向量梯度计算
def test04():
    # 定义需要计算梯度的张量
    x1 = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64, device='cuda')
    x2 = torch.tensor([30, 40], requires_grad=True, dtype=torch.float64, device='cuda')
    # 经过中间的计算
    y = x1 ** 2 + x2 ** 2 + x1 * x2
    print(y)
    # 将输出结果变为标量
    y = y.mean()
    print(y)
    # 自动微分
    y.backward()
    # 打印两个变量的梯度
    print(x1.grad, x2.grad)

输出：

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py 
tensor([1300., 2800.], device='cuda:0', dtype=torch.float64,
       grad_fn=<AddBackward0>)
tensor(2050., device='cuda:0', dtype=torch.float64, grad_fn=<MeanBackward0>)
tensor([25., 40.], device='cuda:0', dtype=torch.float64) tensor([35., 50.], device='cuda:0', dtype=torch.float64)

Process finished with exit code 0

梯度计算细节：

1. 定义函数$(y)$：$[y=x_1^2+x_2^2+x_1\cdot x_2]$

具体计算每个元素：

• 第一个元素： $(10^2+30^2+10\cdot 30=100+900+300=1300)$
• 第二个元素： $(20^2+40^2+20\cdot 40=400+1600+800=2800)$

所以$(y=[1300,2800])$

2. 将结果转换为标量：$[y_{\text{mean}}=\frac{1}{2}\sum y=\frac{1}{2}(1300+2800)=\frac{4100}{2}=2050]$
3. 计算梯度：

• 对 $(x_1)$ 的梯度 ：$[\frac{\partial y_{\text{mean}}}{\partial x_1}=\frac{1}{2}\left(2x_1+x_2\right)]$
• 对第一个元素： $(\frac{1}{2}(2\cdot 10+30)=\frac{1}{2}(20+30)=\frac{50}{2}=25)$
• 对第二个元素：$(\frac{1}{2}(2\cdot 20+40)=\frac{1}{2}(40+40)=\frac{80}{2}=40)$

所以$(x1.grad=[25,40])$

• 对$(x_2)$的梯度：$[\frac{\partial y_{\text{mean}}}{\partial x_2}=\frac{1}{2}\left(2x_2+x_1\right)]$
• 对第一个元素： $(\frac{1}{2}(2\cdot 30+10)=\frac{1}{2}(60+10)=\frac{70}{2}=35)$
• 对第二个元素： $(\frac{1}{2}(2\cdot 40+20)=\frac{1}{2}(80+20)=\frac{100}{2}=50)$

**所以 **$(x2.grad=[35,50])$

3、控制梯度计算

我们可以通过一些方法使得在 requires_grad=True 的张量在某些时候计算不进行梯度计算。
PyTorch 提供了几种方法来实现这一点，包括上下文管理器、装饰器和全局设置。

1. 使用上下文管理器 torch.no_grad()
2. 使用装饰器 torch.no_grad()
3. 使用全局设置 torch.set_grad_enabled(False)

# 1. 控制不计算梯度
def test01():
    x = torch.tensor(10, requires_grad=True, dtype=torch.float64)
    print(x.requires_grad)
    # 第一种方式: 对代码进行装饰
    with torch.no_grad():
        y = x ** 2
    print(y.requires_grad)

    # 第二种方式: 对函数进行装饰
    @torch.no_grad()
    def my_func(x):
        return x ** 2

    print(my_func(x).requires_grad)

    # 第三种方式
    torch.set_grad_enabled(False)
    y = x ** 2
    print(y.requires_grad)

程序运行结果:

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\2-控制梯度计算.py 
True
False
False
False

Process finished with exit code 0

4、累计梯度

累计梯度：每一次训练前，都需要清楚现有梯度，如果不清楚，则会累加。

# 2. 注意: 累计梯度
def test02():
    # 定义需要求导张量
    x = torch.tensor([10, 20, 30, 40], requires_grad=True, dtype=torch.float64)

    for _ in range(3):
        f1 = x ** 2 + 20
        f2 = f1.mean()
        # 默认张量的 grad 属性会累计历史梯度值
        # 所以, 需要我们每次手动清理上次的梯度
        # 注意: 一开始梯度不存在, 需要做判断
        if x.grad is not None:
            x.grad.data.zero_()
        f2.backward()
        print(x.grad)

输出：

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\2-控制梯度计算.py 
tensor([ 5., 10., 15., 20.], dtype=torch.float64)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)

Process finished with exit code 0

如果不清除，梯度值则累加：

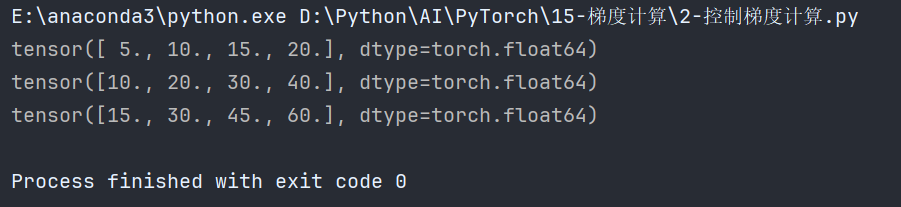
5、梯度下降优化最优解⭐

原理：
梯度下降法是一种优化算法，旨在通过反复调整参数，使目标函数的值达到最小
梯度下降的更新公式为：$[x_{\text{new}}=x_{\text{old}}-\eta \cdot \frac{d}{dx}]$

• $x_{\text{new}}$：更新后的参数值。
• $x_{\text{old}}$：当前的参数值。
• $\eta$：学习率，表示每次更新的步幅的大小。
• $\frac{d}{dx}$：目标函数 $(f)$ 对参数 $(x)$ 的梯度，表示 $(x)$方向上的变化率。

代码：

# 3. 梯度下降优化最优解
def test03():
    # y = x**2
    x = torch.tensor(10, requires_grad=True, dtype=torch.float64)

    for _ in range(5000):
        # 正向计算
        f = x ** 2
        # 梯度清零
        if x.grad is not None:
            x.grad.data.zero_()
        # 反向传播计算梯度
        f.backward()
        # 更新参数
        x.data = x.data - 0.001 * x.grad
        print('%.10f' % x.data)

结果：

1. 第一个结果是：9.9800000000
2. 最后一个结果：0.0004494759

数学解释：

• 初始化参数 $(x)$：$[x=10]$
• 目标函数 $(f)$：$[f(x)=x^2]$
• 计算梯度：$[\frac{d(f)}{d(x)}=2x]$对于初始 $(x=10)$，梯度为 $(2\times 10=20)$。
• 更新参数：$[x_{\text{new}}=x_{\text{old}}-0.001\cdot \frac{d(f)}{d(x)}]$对于初始 $(x=10)$，更新后的 ( x ) 为：$[x_{\text{new}}=10-0.001\times 20=10-0.02=9.98]$

重复更新：
这个过程会在循环中重复多次，每次都根据新的 𝑥x 值计算梯度并更新参数。随着迭代次数的增加，𝑥x 会逐渐减小，最终趋近于 0，这是因为对于函数 𝑓(𝑥)=𝑥2f(x)=x2 而言，最小值在 𝑥=0x=0 处取得。
为什么选择梯度的负方向：
选择梯度的负方向是因为梯度表示函数值增加最快的方向。为了最小化函数，我们需要沿着梯度的反方向移动，即梯度的负方向。
学习率的选择：
学习率 $\eta$ 决定了每次参数更新的步幅大小。选择合适的学习率非常重要：

• 学习率太大：会导致更新步幅过大，可能会跳过最优解，导致发散。
• 学习率太小：会导致更新步幅过小，收敛速度过慢，可能需要更多的迭代次数才能接近最优解。

总结：
梯度下降法是通过反复调整参数，使目标函数的值达到最小的一种优化算法。每次更新参数时，沿着梯度的负方向移动一个步幅，这个步幅由学习率决定。通过这种方式，逐步逼近目标函数的最优解。在实际应用中，选择合适的学习率和迭代次数，对于模型的优化效果至关重要。

6、梯度计算注意事项

当对设置 requires_grad=True 的张量使用 numpy 函数进行转换时, 会出现如下报错：

Can’t call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.

此时, 需要先使用 detach 函数将张量进行分离, 再使用 numpy 函数.
注意：detach 之后会产生一个新的张量, 新的张量作为叶子结点，并且该张量和原来的张量共享数据, 但是分离后的张量不需要计算梯度。

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/20 3:22
import torch


# 1. detach 函数用法
def test01():

    x = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64)

    # Can't call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.
    # print(x.numpy())  # 错误
    print(x.detach().numpy())  # 正确


# 2. detach 前后张量共享内存
def test02():

    x1 = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64)

    # x2 作为叶子结点
    x2 = x1.detach()
    print(x1)
    print(x2)
    # 两个张量的值一样
    # TODO id() 函数用于返回对象的唯一标识符（identity）
    print(id(x1.data), id(x2.data))
    x2.data = torch.tensor([100, 200])
    print(x1)
    print(x2)
    # x2 不会自动计算梯度: False
    print(x2.requires_grad)


if __name__ == '__main__':
    print("test01")
    test01()
    print("test02")
    test02()

程序运行结果:

E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\3-detach.py 
test01
[10. 20.]
test02
tensor([10., 20.], dtype=torch.float64, requires_grad=True)
tensor([10., 20.], dtype=torch.float64)
3035001264464 3035001264464
tensor([10., 20.], dtype=torch.float64, requires_grad=True)
tensor([100, 200])
False

Process finished with exit code 0

不会自动计算梯度：

7、张量转标量的选择⭐

在机器学习和深度学习中，梯度的计算和应用是优化模型的核心部分。

1. 梯度的作用

梯度是指函数在某一点的导数或变化率，表示该点处函数值变化最迅速的方向。
在深度学习中，梯度主要用于以下方面：

①优化模型参数：通过梯度下降法（或其变体），调整模型参数以最小化损失函数。
②反向传播：在训练神经网络时，通过计算损失函数相对于模型参数的梯度，更新参数，使得模型的预测更准确。

2. 为什么梯度的值可以不一样
   梯度的值取决于你选择的损失函数和如何将多维输出转换为标量。

例如，求和和求均值两种方法在将向量转换为标量时会导致不同的梯度值。

3. 均值和求和得到的梯度在作用上的区别
   求和：
   梯度值较大：每个元素的梯度直接反映其对总和的贡献。适用于所有元素的贡献需要累加的情况。
   更新步幅更大：在梯度下降中，更新步幅较大，因为梯度值较大。
   求均值：
   梯度值较小：每个元素的梯度反映其对均值的贡献。适用于考虑整体均衡贡献的情况。
   更新步幅较小：在梯度下降中，更新步幅较小，因为梯度值较小。

总结：

• 梯度的作用：梯度用于优化模型参数，使得损失函数最小化。
• 梯度的值可以不一样：不同的标量化方法（如求和和求均值）会导致不同的梯度值。
• 求和与求均值的区别：求和使梯度较大，更新步幅较大；求均值使梯度较小，更新步幅较小。选择哪种方法取决于具体应用和需求。