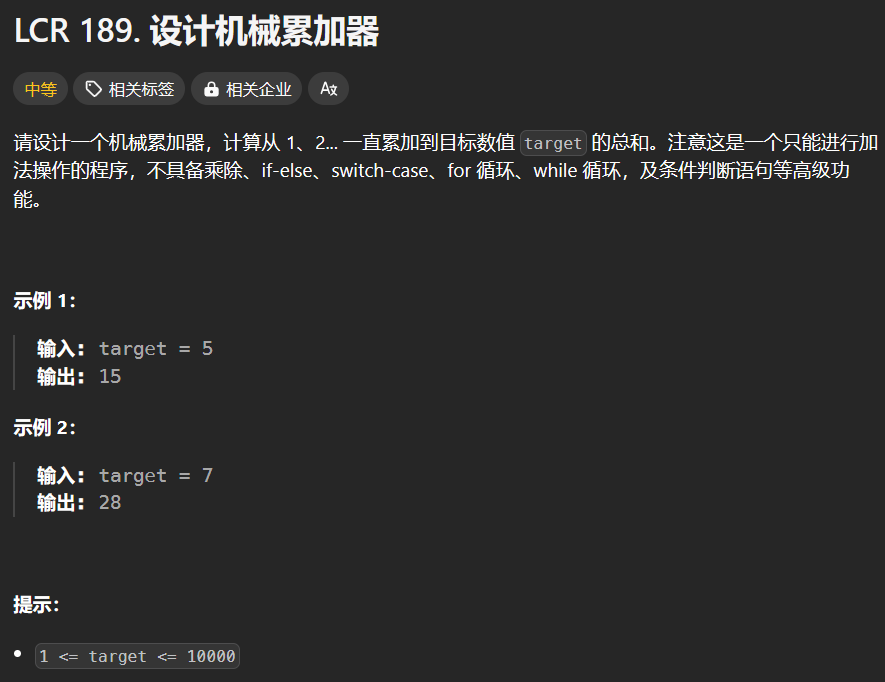
力扣对应题目链接：LCR 189. 设计机械累加器 - 力扣（LeetCode）

牛客对应题目链接：求1+2+3+...+n_牛客题霸_牛客网 (nowcoder.com)

---

一、《剑指Offer》对应内容

---

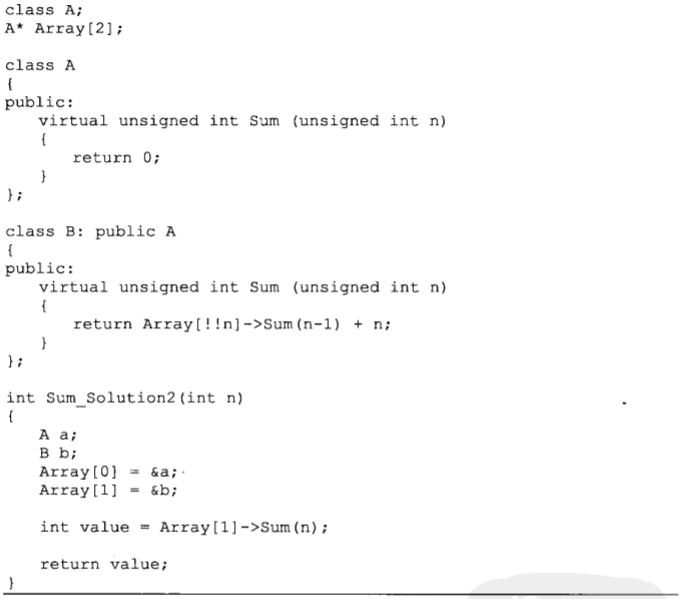
二、分析题目

通常实现递归的时候我们都会利用条件判断语句来决定递归的出口，但由于题目的限制我们不能使用条件判断语句，那么我们就要选择使用别的办法来确定递归出口 —— 逻辑运算符的短路性质。

构造函数：这通过 Temp 类模拟一个累加器，每创建一个 Temp 对象，就将静态成员变量 N 的值累加到 sum 中。在 Solution 类中，通过 mechanicalAccumulator 方法控制累加器的行为：首先重置累加器的状态，然后创建一定数量的 Temp 对象，最后返回累加器累计的结果。也就是每创建一个 Temp 对象，N 就增加 1，然后再将 N 的值加到 sum 中。

上面书中讲到的第四种方法在这里无法实现，因为题目的 n 是动态的，所以无法使用模板类型求解。

---

三、代码

//力扣
//方法一-递归
class Solution {
public:
    int mechanicalAccumulator(int target) {
        return target==0?0:target+mechanicalAccumulator(target-1);
    }
};

//方法二-构造函数
class Temp {
public:
    Temp()
    {
        N++;
        sum+=N;
    }
    static int getSum()
    {
        return sum;
    }
    static void Reset()
    {
        N=0;
        sum=0;
    }
private:
    static int N;
    static int sum;
};

int Temp::N=0;
int Temp::sum=0;

class Solution {
public:
    int mechanicalAccumulator(int target) {
        Temp::Reset();
        Temp* a=new Temp[target];
        delete[] a;
        a=nullptr;
        return Temp::getSum();
    }
};

//方法三-虚函数
class A;
A* Array[2];

class A {
public:
    virtual int sum(int target)
    {
        return 0;
    }
};

class B : public A {
public:
    virtual int sum(int target)
    {
        return Array[!!target]->sum(target-1)+target;
    }
};

class Solution {
public:
    int mechanicalAccumulator(int target) {
        A a;
        B b;
        Array[0]=&a;
        Array[1]=&b;
        return Array[1]->sum(target);
    }
};

//牛客
int i = 1;
int sum = 0;
class Sum
{
public:
    Sum()
    {
        sum += i;
        ++i;
    }
};

class Solution {
public:
    int Sum_Solution(int n) {
        Sum a[n];
        return sum;
    }
};