【科大讯飞笔试题汇总】2024-07-20-科大讯飞秋招提前批(算法岗)-三语言题解(Cpp/Java/Python)

🍭 大家好这里是清隆学长 ，一枚热爱算法的程序员

💻 ACM银牌🥈| 多次AK大厂笔试｜编程一对一辅导

✨ 本系列打算持续跟新 秋招笔试题
👏 感谢大家的订阅➕ 和喜欢💗

📧 清隆这边最近正在收集近一年半互联网笔试题汇总，有需要的小伙伴可以关注文末公主号领取～

文章目录

- 🧷 01.LYA的珠宝展示顺序
- - 问题描述
  - 输入格式
  - 输出格式
  - 样例输入
  - 样例输出
  - 样例说明
  - 数据范围
  - 题解
  - 参考代码
- 🍿 02.LYA的字符串魔法
- - 问题描述
  - 输入格式
  - 输出格式
  - 样例输入
  - 样例输出
  - 样例输入
  - 样例输出
  - 数据范围
  - 题解
  - 参考代码
- 🍡 03.K小姐的幸运数字
- - 问题描述
  - 输入格式
  - 输出格式
  - 样例输入
  - 样例输出
  - 样例说明
  - 数据范围
  - 题解
  - 参考代码
写在最后
- 🎧 秋招陪伴刷题打卡
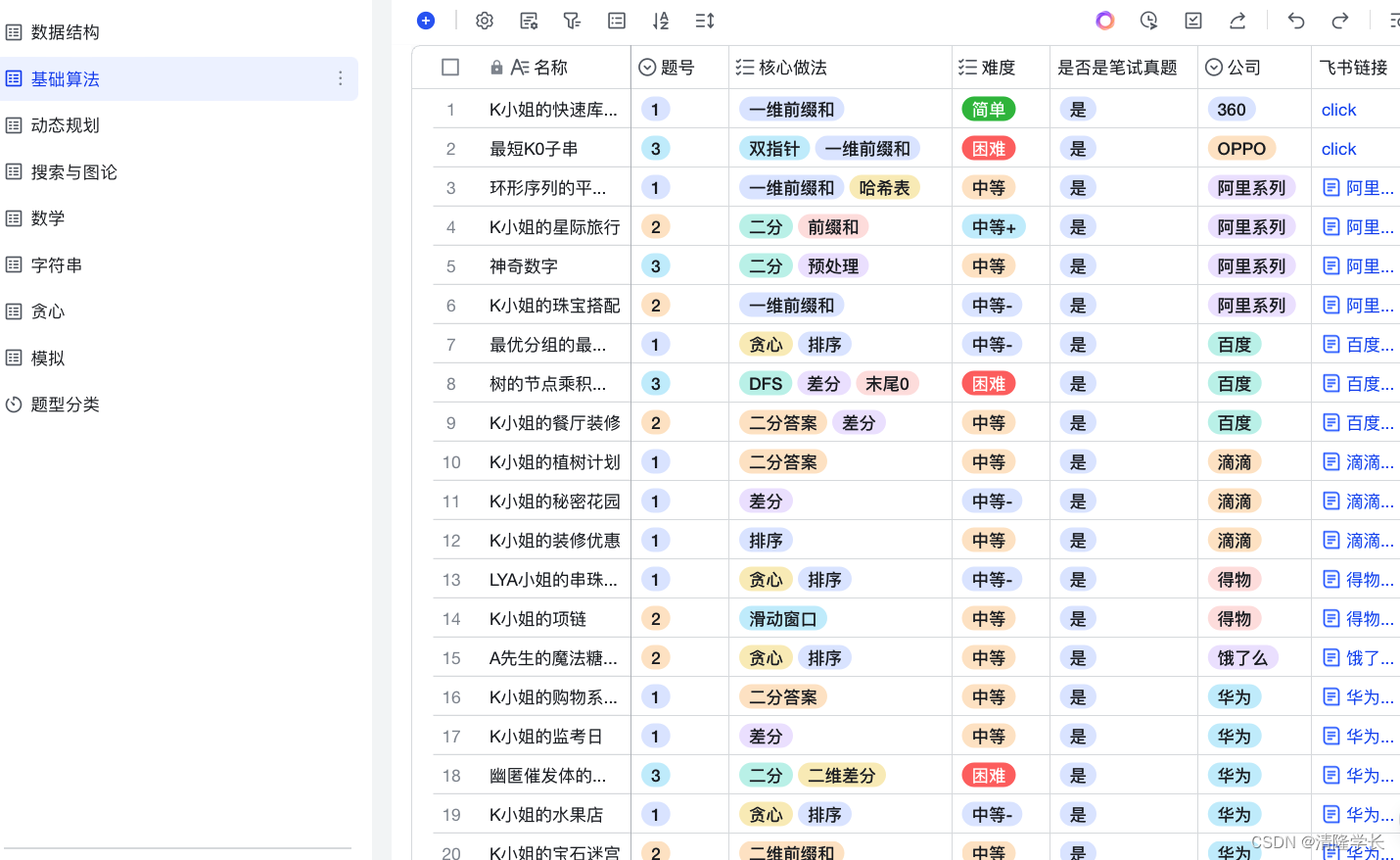
- ✈️ 超全的笔试题汇总

🧷 01.LYA的珠宝展示顺序

问题描述

LYA是一位珠宝设计师，她正在准备一场珠宝展。她有一系列独特的珠宝作品，每件都有其独特的价值。为了让展览更有趣，LYA决定按照特殊的顺序展示她的作品。她想按照以下规则来决定展示顺序：

首先选择价值居中的作品（如果作品数量为奇数）或两个中间价值的作品中较小的一个（如果作品数量为偶数）。
展示选中的作品，并将其从列表中移除。
重复步骤1和2，直到所有作品都被展示。

LYA想知道按照这个规则，她的珠宝作品会以什么顺序被展示。

输入格式

第一行包含一个正整数 $n$ （ $\leq n \leq 10^5$ ），表示珠宝作品的数量。
第二行包含 $n$ 个正整数 $a_1, a_2, ..., a_n$ （ $\leq a_i \leq 10^9$ ），表示每件珠宝作品的价值。

输出格式

输出一行，包含 $n$ 个整数，表示珠宝作品展示的顺序。

样例输入

4
1 9 8 5

样例输出

5 8 1 9

样例说明

首先选择5（两个中间值中较小的一个），然后是8，接着是1，最后是9。

数据范围

$\leq n \leq 10^5$
$\leq a_i \leq 10^9$

题解

找规律+模拟。

首先对输入的价值序列进行排序。
使用两个指针，一个指向序列中间（偶数长度时指向中间偏左），另一个指向中间偏右。
交替输出左指针和右指针指向的元素，并向两端移动指针。

这种方法能够保证每次都选择当前剩余元素中的中位数或两个中间值中较小的一个。

时间复杂度：排序需要 $O(n\log n)$ ，输出需要 $O (n)$ ，总体时间复杂度为 $O(n\log n)$ 。
空间复杂度： $O (n)$ ，用于存储排序后的序列。

参考代码

Python

n = int(input())
a = list(map(int, input().split()))
a.sort()
l, r = (n-1)//2, n//2
result = []
while l >= 0 and r < n:
    if l == r:
        result.append(a[l])
    else:
        result.extend([a[l], a[r]])
    l -= 1
    r += 1
print(*result)

Java

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] a = new int[n];
        for (int i = 0; i < n; i++) {
            a[i] = sc.nextInt();
        }
        Arrays.sort(a);
        int l = (n - 1) / 2, r = n / 2;
        while (l >= 0 && r < n) {
            if (l == r) {
                System.out.print(a[l] + " ");
            } else {
                System.out.print(a[l] + " " + a[r] + " ");
            }
            l--;
            r++;
        }
    }
}

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    sort(a.begin(), a.end());
    int l = (n - 1) / 2, r = n / 2;
    while (l >= 0 && r < n) {
        if (l == r) {
            cout << a[l] << " ";
        } else {
            cout << a[l] << " " << a[r] << " ";
        }
        l--, r++;
    }
    return 0;
}

🍿 02.LYA的字符串魔法

问题描述

LYA 是一位热爱魔法的少女。最近，她发现了一种神奇的字符串魔法。这种魔法可以从一个由小写字母组成的字符串中提取出各种子序列，并计算这些子序列中不同字符的总数。

给定一个长度为 $n$ 的小写字母字符串 $s$ ，LYA 想知道所有非空子序列中不同字符的个数总和是多少。由于这个数字可能非常大，LYA 只需要知道这个总和对 $10^9+7$ 取模后的结果。

你能帮助 LYA 完成这个魔法计算吗？

输入格式

输入一行，包含一个仅由小写字母组成的字符串 $s$ 。

输出格式

输出一个整数，表示所有非空子序列中不同字符的个数总和对 $10^9+7$ 取模后的结果。

样例输入

aaaa

样例输出

样例输入

abcde

样例输出

数据范围

$\leq |s| \leq 10^5$

题解

这道题目的关键在于理解子序列的性质和不同字符的计数方法。

对于字符串中的每个字符，我们需要考虑它在多少个子序列中出现。
假设字符 $c$ 在原字符串中出现了 $k$ 次，那么包含至少一个 $c$ 的子序列数量为 $2^k - 1$ （选择或不选择每个 $c$ ，减去全不选的情况）。
对于不包含 $c$ 的其他位置，有 $2^{n-k}$ 种选择方式。
因此，字符 $c$ 对最终结果的贡献为 $(2^k - 1) \times 2^{n-k}$ 。
我们需要对字符串中的每个不同字符重复这个计算过程，并将结果相加。
最后，将总和对 $10^9+7$ 取模即可得到最终答案。

这种方法的时间复杂度为 $O (n)$ ，其中 $n$ 是字符串的长度。我们只需要遍历一次字符串来统计每个字符的出现次数，然后对每个不同的字符进行一次计算。

参考代码

Python

from collections import Counter

def solve():
    s = input()
    ans = 0
    n = len(s)
    mod = 10**9 + 7
    cnt = Counter(s)
    for c in set(s):
        ans += (pow(2, cnt[c], mod) - 1) * pow(2, n - cnt[c], mod) % mod
        ans %= mod
    print(ans)

if __name__ == '__main__':
    solve()

Java

import java.util.*;

public class Main {
    static final int MOD = 1000000007;

    static long fastPow(long base, int exp) {
        long result = 1;
        while (exp > 0) {
            if ((exp & 1) == 1) {
                result = result * base % MOD;
            }
            base = base * base % MOD;
            exp >>= 1;
        }
        return result;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String s = sc.next();
        int n = s.length();
        long ans = 0;
        int[] cnt = new int[26];
        
        for (char c : s.toCharArray()) {
            cnt[c - 'a']++;
        }
        
        for (int i = 0; i < 26; i++) {
            if (cnt[i] > 0) {
                ans += (fastPow(2, cnt[i]) - 1) * fastPow(2, n - cnt[i]) % MOD;
                ans %= MOD;
            }
        }
        
        System.out.println(ans);
    }
}

#include <iostream>
#include <string>
#include <vector>
using namespace std;

const int MOD = 1e9 + 7;

long long fastPow(long long base, int exp) {
    long long result = 1;
    while (exp > 0) {
        if (exp & 1) {
            result = result * base % MOD;
        }
        base = base * base % MOD;
        exp >>= 1;
    }
    return result;
}

int main() {
    string s;
    cin >> s;
    int n = s.length();
    vector<int> cnt(26, 0);
    long long ans = 0;
    
    for (char c : s) {
        cnt[c - 'a']++;
    }
    
    for (int i = 0; i < 26; i++) {
        if (cnt[i] > 0) {
            ans += (fastPow(2, cnt[i]) - 1) * fastPow(2, n - cnt[i]) % MOD;
            ans %= MOD;
        }
    }
    
    cout << ans << endl;
    return 0;
}

🍡 03.K小姐的幸运数字

问题描述

K小姐是一位数学爱好者,她相信每个人都有自己的幸运数字。最近她发现,任何一个正整数 $n$ 都可以表示成若干个不同的 $2$ 的次幂与 $3$ 的次幂之和的形式，即:

$2^{a_1} \times 3^{b_1} + 2^{a_2} \times 3^{b_2} + \cdots + 2^{a_m} \times 3^{b_m}$

其中 $\leq a_1 < a_2 < \cdots < a_m$ , $\leq b_1 \leq b_2 \leq \cdots \leq b_m$ 。

其中需要满足 $2^{a_i}3^{b_i} \neq 2 ^ {a_j}3^{b_j}$

现在，K小姐希望你能帮她找到给定正整数 $n$ 的这样一个表示法，并将其中的 $m$ 个不同的整数 $\{2^{a_1}3^{b_1}, 2^{a_2}3^{b_2}, \cdots, 2^{a_m}3^{b_m}\}$ 从大到小依次输出。

输入格式

第一行包含一个正整数 $T$ ，表示测试数据的组数。

接下来 $T$ 行,每行包含一个正整数 $n$ ( $\leq n \leq 10^9$ ),表示给定的初始数字。

输出格式

对于每组测试数据，第一行输出一个正整数 $m$ ( $\leq m \leq 100$ ),表示 $2$ 的次幂项的个数。

第二行按照从大到小的顺序输出 $m$ 个不同的整数 $\{2^{a_1}3^{b_1}, 2^{a_2}3^{b_2}, \cdots, 2^{a_m}3^{b_m}\}$ ，相邻两项之间用一个空格隔开。

如果存在多种合法的表示法，你可以输出任意一种。

样例输入

样例输出

样例说明

$\times 3 ^ 0 + 2 ^ 1 \times 3 ^ 0$

$\times 3 ^ 1 + 2 ^ 0 \times 3 ^ 1$

$\times 3 ^ 1 + 2 ^ 3 \times 3 ^ 1 + 2 ^ 0 \times 3 ^ 1$

$\times 3 ^ 1 + 2 ^ 1 \times 3 ^ 1 + 2 ^ 0 \times 3 ^ 1$

$\times 3 ^ 2 + 2 ^ 3 \times 3 ^ 1 + 2 ^ 1 \times 3 ^ 1+ 2 ^ 0 \times 3 ^ 1$

数据范围

$\leq T \leq 100$
$\leq n \leq 10^9$

题解

这题可以直接取巧，我们可以发现，要找到给定正整数 $n$ 的 $2$ 的次幂与 $3$ 的次幂之和表示，实际上可以直接将 $n$ 进行二进制拆分。因为 $2$ 的次幂就对应二进制中的 $1$ ，而 $3$ 的次幂我们可以先不管。

这样做的时间复杂度为 $O(\log n)$ ,空间复杂度为 $O(\log n)$ 。

参考代码

Python

T = int(input())
for _ in range(T):
    n = int(input())
    v = []
    for i in range(32):
        if (n >> i) & 1:
            v.append(1 << i)
    m = len(v)
    print(m)
    print(*v[::-1])

Java

import java.util.*;

public class Main {
    public static void solve(Scanner sc) {
        int n = sc.nextInt();
        List<Integer> v = new ArrayList<>();
        for (int i = 0; i < 32; i++) {
            if ((n >> i & 1) == 1) {
                v.add(1 << i);
            }
        }
        int m = v.size();
        System.out.println(m);
        for (int i = m - 1; i >= 0; i--) {
            System.out.print(v.get(i));
            if (i > 0) {
                System.out.print(" ");
            }
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();
        while (T-- > 0) {
            solve(sc);
        }
    }
}

#include <iostream>
#include <vector>
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> v;
    for (int i = 0; i < 32; i++) {
        if (n >> i & 1) {
            v.push_back(1 << i);
        }
    }
    int m = v.size();
    cout << m << endl;
    for (int i = m - 1; i >= 0; i--) {
        cout << v[i];
        if (i > 0) {
            cout << " ";
        }
    }
    cout << endl;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}